15.3公式法因式分解
图片预览






文档简介
(共19张PPT)
庄河第十六初级中学 崔英军
《数学》 人教版 八年级上册
感知身边的数学
993-99能被100整除吗
问题1.什么叫多项式的因式分解
问题2.y2-25能用提公因式法分解因式吗
计算下列各题:
(1) (x+ 1)(x– 1)
(2) (x+m)(x m)
(3)(2y+5)(2y 5)
(4) (a+b)(a b)
=x2 1 ;
=x2 m2 ;
=4y2 25 ;
=a2 b2 .
以上的运算可直接用乘法公式:
(a+b)(a-b)=a2-b2
我们把平方差公式反过来,得
a2-b2 = (a+b)(a-b)
探索新知的乐趣
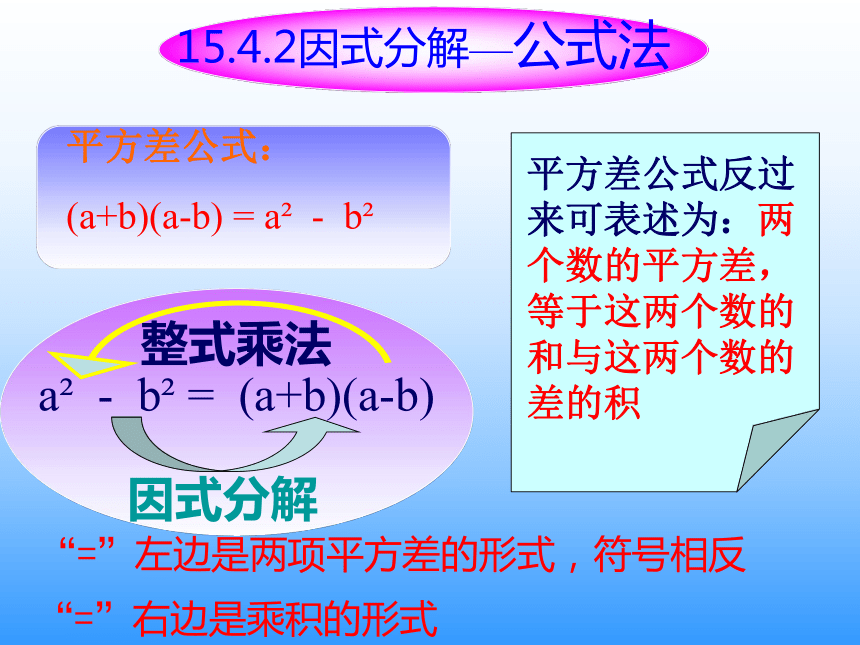
平方差公式反过来可表述为:两个数的平方差,等于这两个数的和与这两个数的差的积
a - b = (a+b)(a-b)
因式分解
平方差公式:
(a+b)(a-b) = a - b
整式乘法
15.4.2因式分解—公式法
“=”左边是两项平方差的形式,符号相反
“=”右边是乘积的形式
1判断下列多项式是否可以用平方差公式分解因式?可以的话指出公式中的a和b。
(1) 4x2+y2 (2) x2-0.64
(3) -4x2-y2 (4) -4x2+y2
(5) (m+n)2-4 (6) a2-b2+3
小思考
×
∨
×
∨
∨
×
例1、把下列多项式分解因式。
⑴、25-16x2
⑵、-b2+ 9a2
a2
b2
=( + )( - )
=(5+ 4x)(5-4x)
=(3a)2-b2
解:原式= 52 -(4x)2
=(3a+b)(3a-b)
从以上这两题可以发现: 确定多项式中的 和 是利用平方差公式分解因式的关键.
a
b
(a+b)
(a-b)
解:原式=9a2-b2
利用 平方差公式分解因式的步骤:
1. 确定 公式中的a 和 b.
2. 变成a2 -b2 的形式
3. 根据a2-b2=(a+b)(a-b)写出结果即可.
做一做
1下列利用公式法分解因式正确的是( )
A)4a2-c2=(4a-c)(4a+c)
B) -b2+1 =(-b+1)(-b-1)
C) -m2n2+482=(48+mn)(48-mn)
D) -y2+9x2=(x+3y)(x-3y)
C
2将下面 的多项式分解因式
m - 16
2) 4x - 9y
3) -25 + 36b2
4) - 0.49p2+c2
做一做
=(m+4)(m-4)
=(2x+3y)(2x-3y)
=(6b+5)(6b-5)
=(c+0.7)(c-0.7)
例2、把下列多项式分解因式。
(x+p)2-(x+q)2
解:原式
=[(x+p)+(x+q)][(x+p)-(x+q)]
=( x+p+x+q)( x+p-x-q)
=(2 x+p+q)(p-q)
( ) 2
( )2
a2
b2
x+p
x+q
把下列各式因式分解
1)( x + z ) - ( y + z )
2)4( a + b) - 25 a
解:
1.原式=[(x+z)+(y+z)][(x+z)-(y+z)]
=(x+y+2z)(x-y)
2.原式=[2(a+b)] -(5a)
=[2(a+b)+ 5a][2(a+b)- 5a]
=(7a+2b)(2b-3a)
例3、把下列多项式分解因式。
解:原式=3a(a2-9)
=3a(a+3)(a-3)
1)3a3-27a
因式分解的步骤是首先提取公因式,然后考虑用公式.
分解因式必须进行到每一个多项式都不能再分解为止
2) x4-y4
解:原式=(x2)2-(y2)2
=(x2+y2)(x2-y2)
=(x2+y2)(x+y)(x-y)
把下列各式因式分解
3a3 - 48ab2
x2y - 4y
3)-x4+81
解:
1.原式=3a(a2-16b2)
=3a(a+4b)(a-4b)
解:原式=y(x2-4)
=y(x+2)(x-2)
解:原式
=92-(x2)2
=(9+x2)(9-x2)
=(9+x2)(3+x)(3-x)
注意:最终结果
要保证不能再分
解为止,也就是说
分解要彻底.
聪明屋
993-99能被100整除吗 你是怎样想的 与同伴交流.
解 ∵993-99=99 ×(992-1)
=99 (99+1)(99-1)
= 99×100×98
∴ 993-99能被100整除。
分享你我收获
通过本节课的学习:
对自己说,你有哪些收获
对同学说,你有哪些温馨提示
对老师说,你有哪些疑惑
开拓崭新天地
1作业:
教科书习题15.4第2,11题.
创新与应用
1已知x+ y =7, x-y =5
求代数式 x 2- y2-2y+2x 的值.
2 求方程的x -y =15的正整数解
谢谢,再见!
愿你能自由翱翔于知识的天空
庄河第十六初级中学 崔英军
《数学》 人教版 八年级上册
感知身边的数学
993-99能被100整除吗
问题1.什么叫多项式的因式分解
问题2.y2-25能用提公因式法分解因式吗
计算下列各题:
(1) (x+ 1)(x– 1)
(2) (x+m)(x m)
(3)(2y+5)(2y 5)
(4) (a+b)(a b)
=x2 1 ;
=x2 m2 ;
=4y2 25 ;
=a2 b2 .
以上的运算可直接用乘法公式:
(a+b)(a-b)=a2-b2
我们把平方差公式反过来,得
a2-b2 = (a+b)(a-b)
探索新知的乐趣
平方差公式反过来可表述为:两个数的平方差,等于这两个数的和与这两个数的差的积
a - b = (a+b)(a-b)
因式分解
平方差公式:
(a+b)(a-b) = a - b
整式乘法
15.4.2因式分解—公式法
“=”左边是两项平方差的形式,符号相反
“=”右边是乘积的形式
1判断下列多项式是否可以用平方差公式分解因式?可以的话指出公式中的a和b。
(1) 4x2+y2 (2) x2-0.64
(3) -4x2-y2 (4) -4x2+y2
(5) (m+n)2-4 (6) a2-b2+3
小思考
×
∨
×
∨
∨
×
例1、把下列多项式分解因式。
⑴、25-16x2
⑵、-b2+ 9a2
a2
b2
=( + )( - )
=(5+ 4x)(5-4x)
=(3a)2-b2
解:原式= 52 -(4x)2
=(3a+b)(3a-b)
从以上这两题可以发现: 确定多项式中的 和 是利用平方差公式分解因式的关键.
a
b
(a+b)
(a-b)
解:原式=9a2-b2
利用 平方差公式分解因式的步骤:
1. 确定 公式中的a 和 b.
2. 变成a2 -b2 的形式
3. 根据a2-b2=(a+b)(a-b)写出结果即可.
做一做
1下列利用公式法分解因式正确的是( )
A)4a2-c2=(4a-c)(4a+c)
B) -b2+1 =(-b+1)(-b-1)
C) -m2n2+482=(48+mn)(48-mn)
D) -y2+9x2=(x+3y)(x-3y)
C
2将下面 的多项式分解因式
m - 16
2) 4x - 9y
3) -25 + 36b2
4) - 0.49p2+c2
做一做
=(m+4)(m-4)
=(2x+3y)(2x-3y)
=(6b+5)(6b-5)
=(c+0.7)(c-0.7)
例2、把下列多项式分解因式。
(x+p)2-(x+q)2
解:原式
=[(x+p)+(x+q)][(x+p)-(x+q)]
=( x+p+x+q)( x+p-x-q)
=(2 x+p+q)(p-q)
( ) 2
( )2
a2
b2
x+p
x+q
把下列各式因式分解
1)( x + z ) - ( y + z )
2)4( a + b) - 25 a
解:
1.原式=[(x+z)+(y+z)][(x+z)-(y+z)]
=(x+y+2z)(x-y)
2.原式=[2(a+b)] -(5a)
=[2(a+b)+ 5a][2(a+b)- 5a]
=(7a+2b)(2b-3a)
例3、把下列多项式分解因式。
解:原式=3a(a2-9)
=3a(a+3)(a-3)
1)3a3-27a
因式分解的步骤是首先提取公因式,然后考虑用公式.
分解因式必须进行到每一个多项式都不能再分解为止
2) x4-y4
解:原式=(x2)2-(y2)2
=(x2+y2)(x2-y2)
=(x2+y2)(x+y)(x-y)
把下列各式因式分解
3a3 - 48ab2
x2y - 4y
3)-x4+81
解:
1.原式=3a(a2-16b2)
=3a(a+4b)(a-4b)
解:原式=y(x2-4)
=y(x+2)(x-2)
解:原式
=92-(x2)2
=(9+x2)(9-x2)
=(9+x2)(3+x)(3-x)
注意:最终结果
要保证不能再分
解为止,也就是说
分解要彻底.
聪明屋
993-99能被100整除吗 你是怎样想的 与同伴交流.
解 ∵993-99=99 ×(992-1)
=99 (99+1)(99-1)
= 99×100×98
∴ 993-99能被100整除。
分享你我收获
通过本节课的学习:
对自己说,你有哪些收获
对同学说,你有哪些温馨提示
对老师说,你有哪些疑惑
开拓崭新天地
1作业:
教科书习题15.4第2,11题.
创新与应用
1已知x+ y =7, x-y =5
求代数式 x 2- y2-2y+2x 的值.
2 求方程的x -y =15的正整数解
谢谢,再见!
愿你能自由翱翔于知识的天空
