作轴对称图形
图片预览




文档简介
(共23张PPT)
由一个平面图形得到它的轴对称的图形叫做轴对称变换。
轴对称变换
轴对称变换不会改变图形的 和
,只会改变图形 。
大小
位置
形状
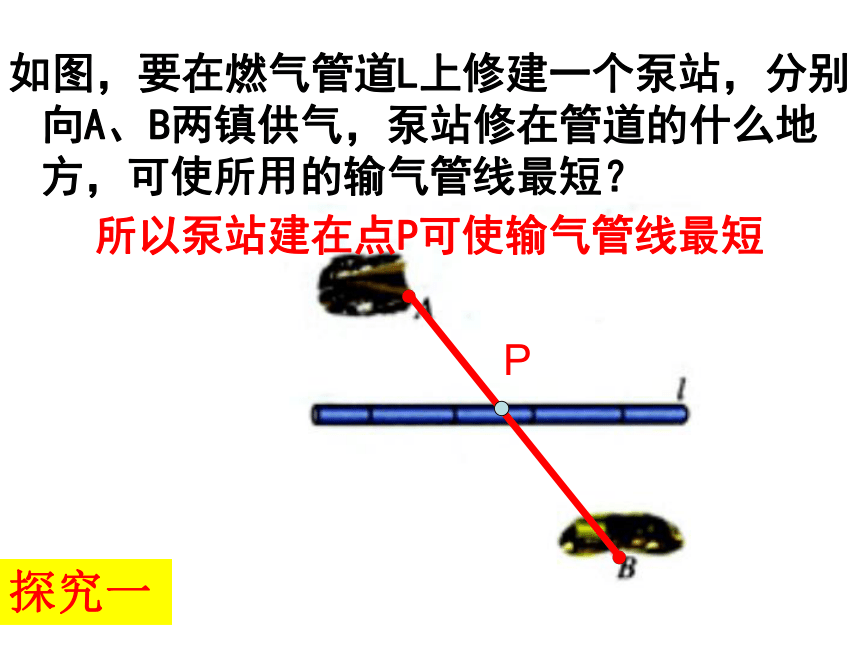
如图,要在燃气管道L上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?
P
所以泵站建在点P可使输气管线最短
探究一
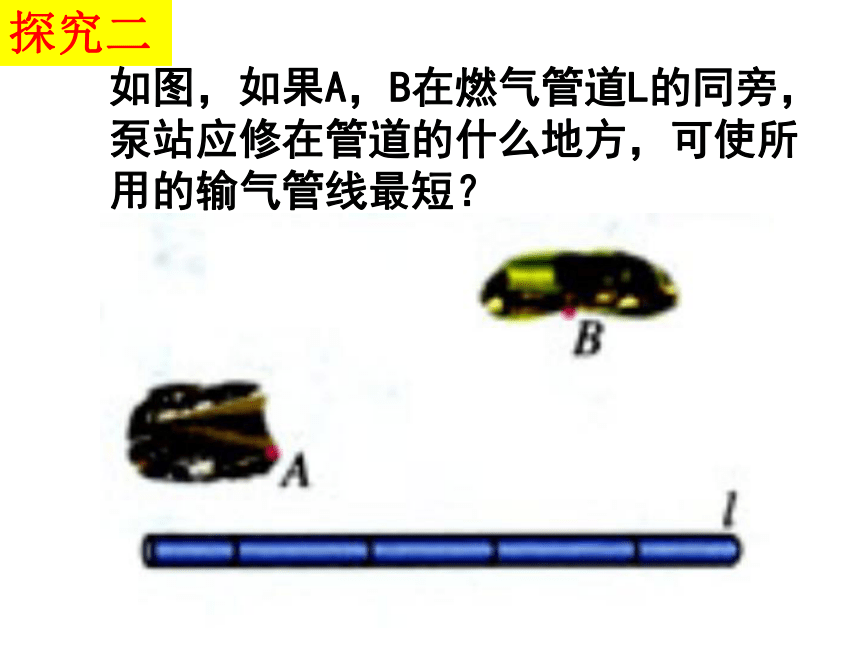
如图,如果A,B在燃气管道L的同旁,泵站应修在管道的什么地方,可使所用的输气管线最短?
探究二
思考???
为什么在P点的位置修建泵站,就能使所用的管线最短呢?
总结经验:
实际上是通过轴对称变换,把A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”加以解决。
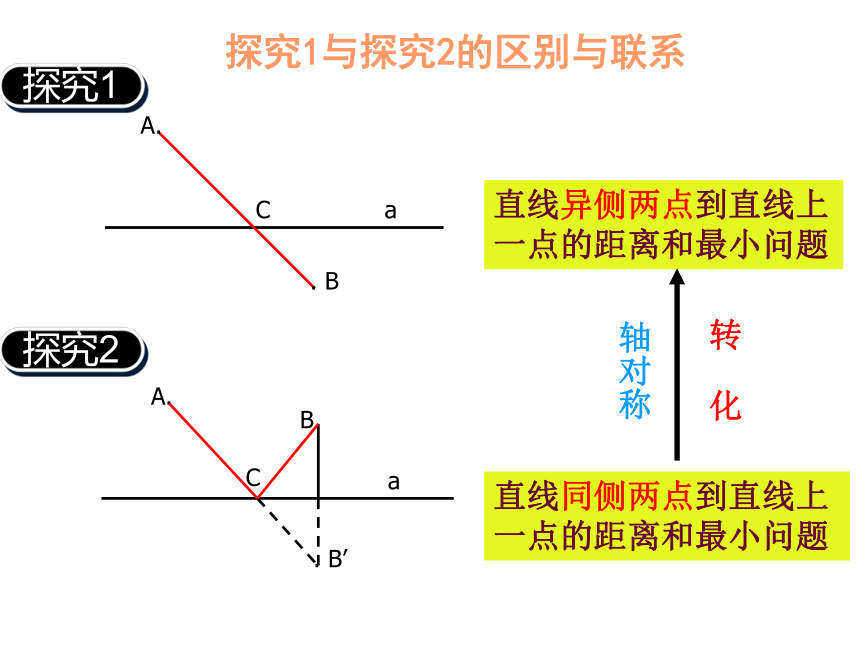
直线同侧两点到直线上一点的距离和最小问题
直线异侧两点到直线上一点的距离和最小问题
轴对称
转 化
探究1与探究2的区别与联系
探究1
C
A.
. B
a
探究2
A.
B.
. B’
C
a
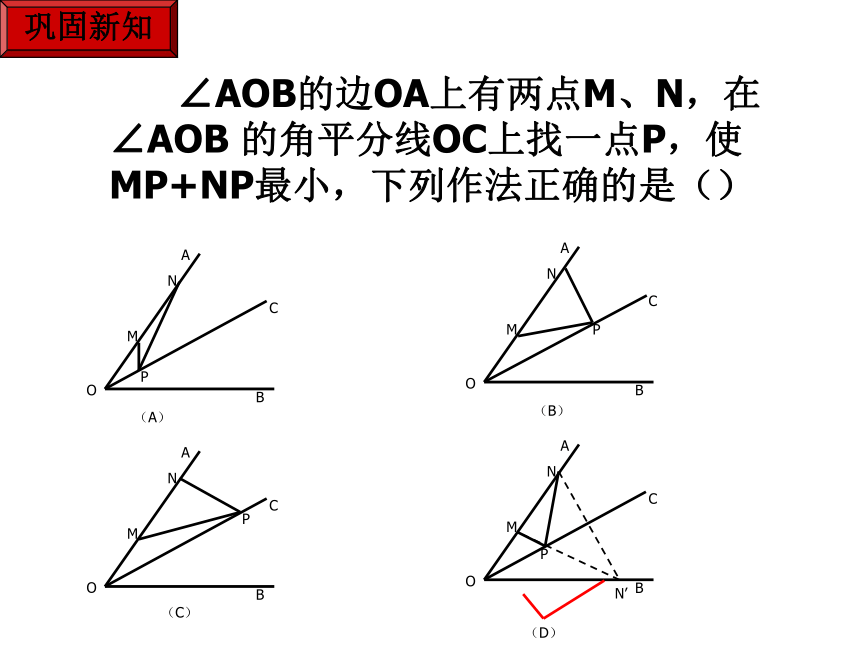
∠AOB的边OA上有两点M、N,在∠AOB 的角平分线OC上找一点P,使MP+NP最小,下列作法正确的是()
O
B
A
M
N
C
O
B
A
M
N
C
O
B
A
M
N
C
O
B
A
M
N
C
P
P
P
P
N’
(A)
(D)
(C)
(B)
巩固新知
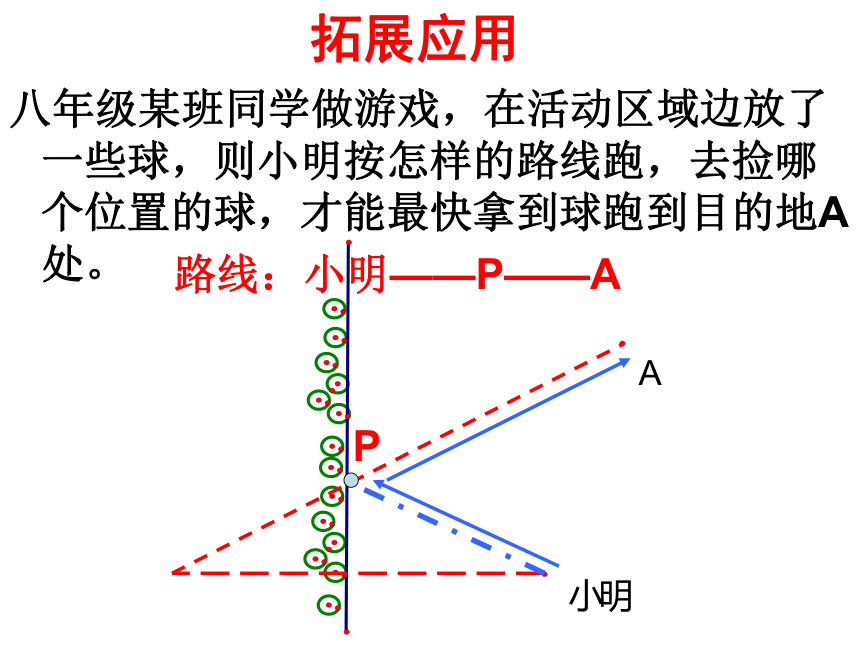
拓展应用
八年级某班同学做游戏,在活动区域边放了一些球,则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A处。
P
路线:小明——P——A
如果另一侧放着一些小木棍,小明先去捡球,还要跑到另一侧去取木棍,则小明又应按怎样的路线跑,去捡哪个位置的球,小木棍,才能最快跑到目的地A处。
D
E
C
路线:小明——D——E——A
如图,A为马厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边给马喝水,然后回到帐篷,请你帮助他确定这一天的最短路线。
如果我们把台球桌做成等边三角形的形状,那么从AC中点D处发出的球,能否依次经BC、AB两条边反射回到D处?如果你认为不能,请说明理由;如果你认为能,请作出球运动的路线。
A
B
C
D
在平面直角坐标系中画出下列各点关于x轴的对称点.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B’ (-4, -2)
·
C’(3, 4)
思考:关于x轴对称的点的坐标具有怎样的关系?
x
y
通过探究你能用语言归纳关于 x 轴对称的点坐标规律吗?
探究2:如图,你能在平面直角坐标系中画出点A关于y轴的对称点A’吗
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
·
A’(-2,3)
你能说出点A与点A’坐标的关系吗?
x
y
练习:
1、点P(-5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2、点M (a, -5)与点N(-2, b)关于x轴对称,则a=_____, b =_____.
3、点P(-5, 6)与点Q关于y轴对称,则点Q的坐标为__________.
4、点M (a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
小结:在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
点(x, y)关于x轴对称的点的坐标为______.
点(x, y)关于y轴对称的点的坐标为______.
(x, - y)
(- x, y)
已知点关于x轴或y轴对称的点的坐标变化规律:
1、完成下表.
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴的对称点
关于y轴的对称点
(-2, -3)
(2, 3)
(-1,-2)
(1, 2)
(6, -5)
(-6, 5)
(0, -1.6)
(0,1.6)
(-4,0)
(4,0)
2、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
练 习
2
4
6
-20
(抢答)
例:已知△ABC的三个顶点的坐标分别为A
(-3,5),B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。
解:点A(-3,5),B(-4,1),
C(-1,3),关于y轴对称
点的坐标分别为A’(3,5), B’(4,1),C’(1,3).依次连接A’B’,B’C’,C’A’,就得到△ABC关于y轴对称的△A’B’C’.
·
·
·
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
c
B
B’
A’
C’
归纳:(P44)先求出已知图形中的 特殊点(如多边形的顶点或端点)的对应点的坐标,描出并连接这些点,就可 得到这个图形的轴对称图形.
x
y
练习:P45 2 .3
(1,2)
·
·
·
·
·
·
(拓展提高)
思考:如图,分别作出点P,M,N关于直线x=1的对称点, 你能发现它们坐标之间分别有什么关系吗
3
1
4
2
5
-2
-1
0
1
2
3
4
5
-4
-3
-2
-1
x=1
·
·
·
·
·
·
P(-2,4)
M(-1,1)
N’(5,-2)
N(-3,-2)
M’(3,1)
P’(4,4)
15
x
y
,
’
类似: 若两点(x1,y1)、(x2,y2)关于
直线y=n对称,则 ;
归纳:若两点(x1,y1)、(x2,y2)关于 直线
x=m对称,则:
y1=y2
x1=x2
X2=2m-x1
y2=2n-y1
(m= )
(n= )
本节课你有哪些收获?
由一个平面图形得到它的轴对称的图形叫做轴对称变换。
轴对称变换
轴对称变换不会改变图形的 和
,只会改变图形 。
大小
位置
形状
如图,要在燃气管道L上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?
P
所以泵站建在点P可使输气管线最短
探究一
如图,如果A,B在燃气管道L的同旁,泵站应修在管道的什么地方,可使所用的输气管线最短?
探究二
思考???
为什么在P点的位置修建泵站,就能使所用的管线最短呢?
总结经验:
实际上是通过轴对称变换,把A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”加以解决。
直线同侧两点到直线上一点的距离和最小问题
直线异侧两点到直线上一点的距离和最小问题
轴对称
转 化
探究1与探究2的区别与联系
探究1
C
A.
. B
a
探究2
A.
B.
. B’
C
a
∠AOB的边OA上有两点M、N,在∠AOB 的角平分线OC上找一点P,使MP+NP最小,下列作法正确的是()
O
B
A
M
N
C
O
B
A
M
N
C
O
B
A
M
N
C
O
B
A
M
N
C
P
P
P
P
N’
(A)
(D)
(C)
(B)
巩固新知
拓展应用
八年级某班同学做游戏,在活动区域边放了一些球,则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A处。
P
路线:小明——P——A
如果另一侧放着一些小木棍,小明先去捡球,还要跑到另一侧去取木棍,则小明又应按怎样的路线跑,去捡哪个位置的球,小木棍,才能最快跑到目的地A处。
D
E
C
路线:小明——D——E——A
如图,A为马厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边给马喝水,然后回到帐篷,请你帮助他确定这一天的最短路线。
如果我们把台球桌做成等边三角形的形状,那么从AC中点D处发出的球,能否依次经BC、AB两条边反射回到D处?如果你认为不能,请说明理由;如果你认为能,请作出球运动的路线。
A
B
C
D
在平面直角坐标系中画出下列各点关于x轴的对称点.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B’ (-4, -2)
·
C’(3, 4)
思考:关于x轴对称的点的坐标具有怎样的关系?
x
y
通过探究你能用语言归纳关于 x 轴对称的点坐标规律吗?
探究2:如图,你能在平面直角坐标系中画出点A关于y轴的对称点A’吗
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
·
A’(-2,3)
你能说出点A与点A’坐标的关系吗?
x
y
练习:
1、点P(-5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2、点M (a, -5)与点N(-2, b)关于x轴对称,则a=_____, b =_____.
3、点P(-5, 6)与点Q关于y轴对称,则点Q的坐标为__________.
4、点M (a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
小结:在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
点(x, y)关于x轴对称的点的坐标为______.
点(x, y)关于y轴对称的点的坐标为______.
(x, - y)
(- x, y)
已知点关于x轴或y轴对称的点的坐标变化规律:
1、完成下表.
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴的对称点
关于y轴的对称点
(-2, -3)
(2, 3)
(-1,-2)
(1, 2)
(6, -5)
(-6, 5)
(0, -1.6)
(0,1.6)
(-4,0)
(4,0)
2、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
练 习
2
4
6
-20
(抢答)
例:已知△ABC的三个顶点的坐标分别为A
(-3,5),B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。
解:点A(-3,5),B(-4,1),
C(-1,3),关于y轴对称
点的坐标分别为A’(3,5), B’(4,1),C’(1,3).依次连接A’B’,B’C’,C’A’,就得到△ABC关于y轴对称的△A’B’C’.
·
·
·
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
c
B
B’
A’
C’
归纳:(P44)先求出已知图形中的 特殊点(如多边形的顶点或端点)的对应点的坐标,描出并连接这些点,就可 得到这个图形的轴对称图形.
x
y
练习:P45 2 .3
(1,2)
·
·
·
·
·
·
(拓展提高)
思考:如图,分别作出点P,M,N关于直线x=1的对称点, 你能发现它们坐标之间分别有什么关系吗
3
1
4
2
5
-2
-1
0
1
2
3
4
5
-4
-3
-2
-1
x=1
·
·
·
·
·
·
P(-2,4)
M(-1,1)
N’(5,-2)
N(-3,-2)
M’(3,1)
P’(4,4)
15
x
y
,
’
类似: 若两点(x1,y1)、(x2,y2)关于
直线y=n对称,则 ;
归纳:若两点(x1,y1)、(x2,y2)关于 直线
x=m对称,则:
y1=y2
x1=x2
X2=2m-x1
y2=2n-y1
(m= )
(n= )
本节课你有哪些收获?
