3.校园风景 课件(25张PPT)
图片预览








文档简介
校园是同学们学习生活的地方,校园里的角角落落用审美的眼光去观察,就会发现很多景物都是一幅幅美丽的画卷。
思考:
怎么用画笔诠释这些画卷?
如何在平面上反应出三维的物体形状?
想要在二维的平面上反映出三维的物体形状,就得依靠透视学的帮助。
怎么在平面上反应出三维的物体形状?
校园风景
——透视原理
透视——
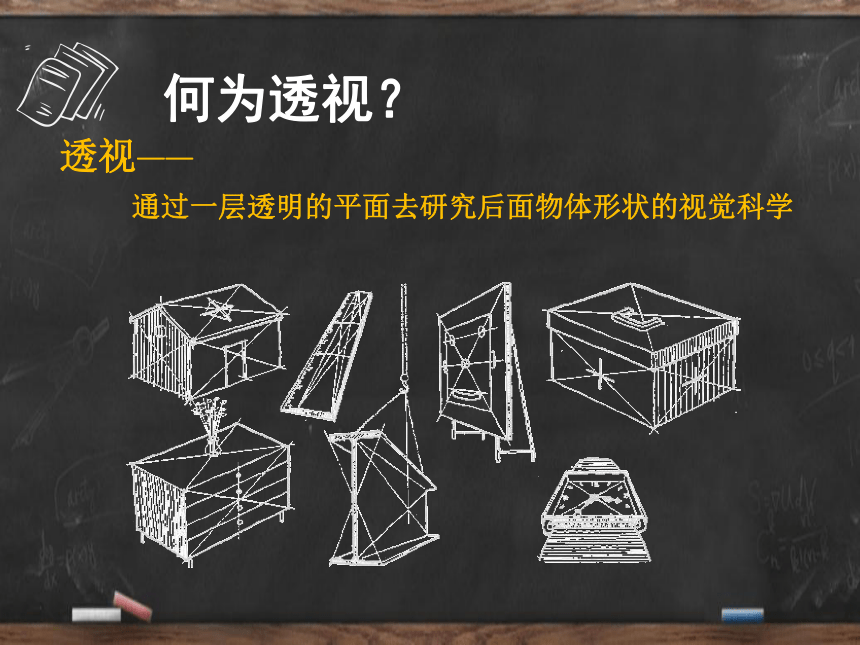
通过一层透明的平面去研究后面物体形状的视觉科学
何为透视?
视平线
视觉平行线,与人眼等高的一条线
观察并思考,下面两幅图所表现的景物空间有什么特点?
霍贝玛《林间小道》
消失点
近大远小
可以从图中看出正六面体的线段有水平线、垂直线其中有四条与画面垂直的线段,还有四条边线的延伸虚线,这四条边线向A点消失。我们把这样的透视称之为一点透视。也叫平行透视。
结论:
A
活动一
各小组讨论绘画:分别画出物体在不同方位的一点透视图。
平行透视:
一个消失点 有一个面对着自己 竖线垂直
在课室中存在的平行透视
《最后的晚餐》被列为绘画透视学的经典之作
没有任何一对平面与画面平行,而是形成一定的角度,并且水平放置与地面垂直。便构成了成角状态。(两个面一个角面对自己,前面近后面远,形成两个消失点。)
成角透视:
《相对性》 埃舍尔 石版画
《画廊》 埃舍尔 石版画
活动二
画一画:利用透视规律,简单表现立体空间的作品。
通过刚才的学习,请同学们讨论比较总结平行透视和成角透视各有什么样的消失规律?
比一比
平行透视
成角透视
点
比一比
一个消失点
有一个面对着自己
竖线垂直
平行透视
成角透视
两个消失点
有一个角对着自己
竖线垂直
小结:
点
留意我们身边的透视现象,
用相机或画笔记录下来
做个生活的有心人!
拓展延伸:
Thank you
思考:
怎么用画笔诠释这些画卷?
如何在平面上反应出三维的物体形状?
想要在二维的平面上反映出三维的物体形状,就得依靠透视学的帮助。
怎么在平面上反应出三维的物体形状?
校园风景
——透视原理
透视——
通过一层透明的平面去研究后面物体形状的视觉科学
何为透视?
视平线
视觉平行线,与人眼等高的一条线
观察并思考,下面两幅图所表现的景物空间有什么特点?
霍贝玛《林间小道》
消失点
近大远小
可以从图中看出正六面体的线段有水平线、垂直线其中有四条与画面垂直的线段,还有四条边线的延伸虚线,这四条边线向A点消失。我们把这样的透视称之为一点透视。也叫平行透视。
结论:
A
活动一
各小组讨论绘画:分别画出物体在不同方位的一点透视图。
平行透视:
一个消失点 有一个面对着自己 竖线垂直
在课室中存在的平行透视
《最后的晚餐》被列为绘画透视学的经典之作
没有任何一对平面与画面平行,而是形成一定的角度,并且水平放置与地面垂直。便构成了成角状态。(两个面一个角面对自己,前面近后面远,形成两个消失点。)
成角透视:
《相对性》 埃舍尔 石版画
《画廊》 埃舍尔 石版画
活动二
画一画:利用透视规律,简单表现立体空间的作品。
通过刚才的学习,请同学们讨论比较总结平行透视和成角透视各有什么样的消失规律?
比一比
平行透视
成角透视
点
比一比
一个消失点
有一个面对着自己
竖线垂直
平行透视
成角透视
两个消失点
有一个角对着自己
竖线垂直
小结:
点
留意我们身边的透视现象,
用相机或画笔记录下来
做个生活的有心人!
拓展延伸:
Thank you
