用坐标表示轴对称
图片预览





文档简介
(共23张PPT)
用坐标表示轴对称
人教版八年级数学上册(2课时)
由一个平面图形得到它的轴对称图形,这样的变换叫做图形的轴对称变换
——成轴对称的两个图形的任何一个可以看作由另一个图形经过轴对称变换后得到的;
一个轴对称图形也可以看作以它的一部分为基础,经轴对称变换扩展而成的。
应用:已知一个图形和一条直线,你能作出它的轴对称图形吗?
轴对称变换
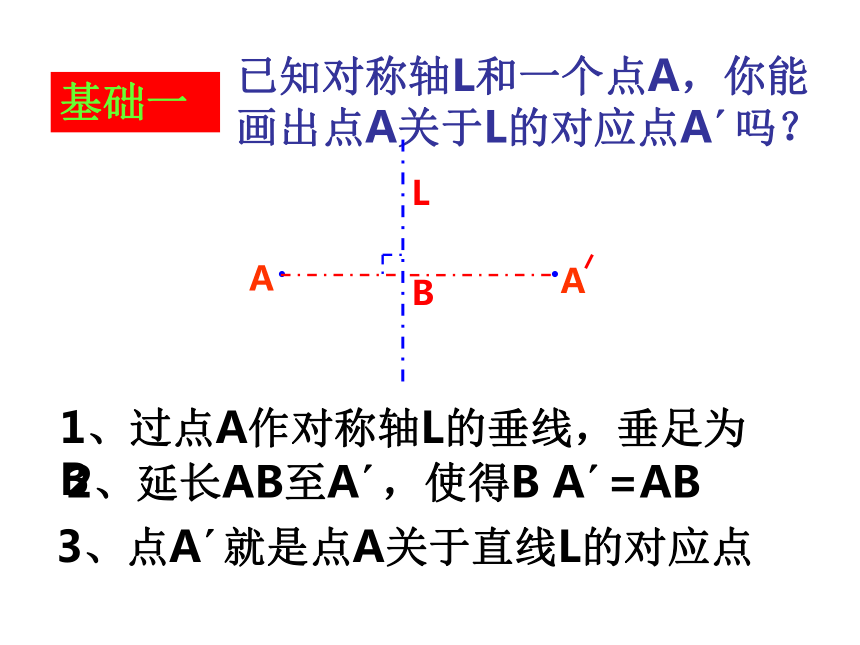
已知对称轴L和一个点A,你能画出点A关于L的对应点A 吗?
A·
L
·
A
1、过点A作对称轴L的垂线,垂足为B
2、延长AB至A ,使得B A =AB
B
3、点A 就是点A关于直线L的对应点
基础一
1、过点A作对称轴L的垂线A A ,使CA=C A
已知对称轴L和一条线段AB,画出线段AB 关于L的对应线段A B 。
A
B
A
B
L
2、过点A作对称轴L的垂线BB ,使DB=DB
3、连接A B ,线段A B 就是关于直线
L的对应线段
C
D
基础二
成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到。一个轴对称图形也可以看作以它的一部分为基础,经轴对称变换扩展而得到
基础三
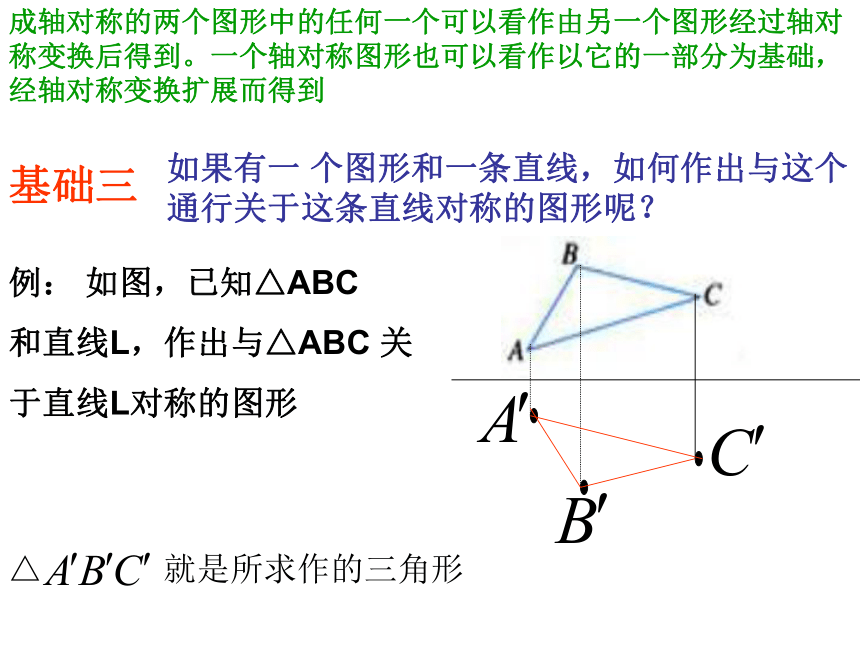
如果有一 个图形和一条直线,如何作出与这个通行关于这条直线对称的图形呢?
例: 如图,已知△ABC
和直线L,作出与△ABC 关
于直线L对称的图形
△ 就是所求作的三角形
已知 ABC和直线m,以直线m为对称轴,作 ABC经的对称图形
B
C
A
作法:1、作AP⊥直线m于P,延长AP至Aˊ,使APˊ=AP,则点Aˊ就是点A关于直线m的对称点,同理点B和点C一样作.
2、连结A’B’,B’C’,CˊAˊ
AˊB’C’即为所求
随堂练习
Aˊ
Bˊ
Cˊ
归纳
(1)几何图形都可以看作由点组成,只要作出这些点关于对称轴的对应点,再连接对应点,就可以得到原图形的轴对称图形
(2)对于一些由直线、线段或射线组成的图形只要作出图形中的一些特殊点的对称点,再连接对应点,就可以得到原图形的轴对称图形
动动手画一画
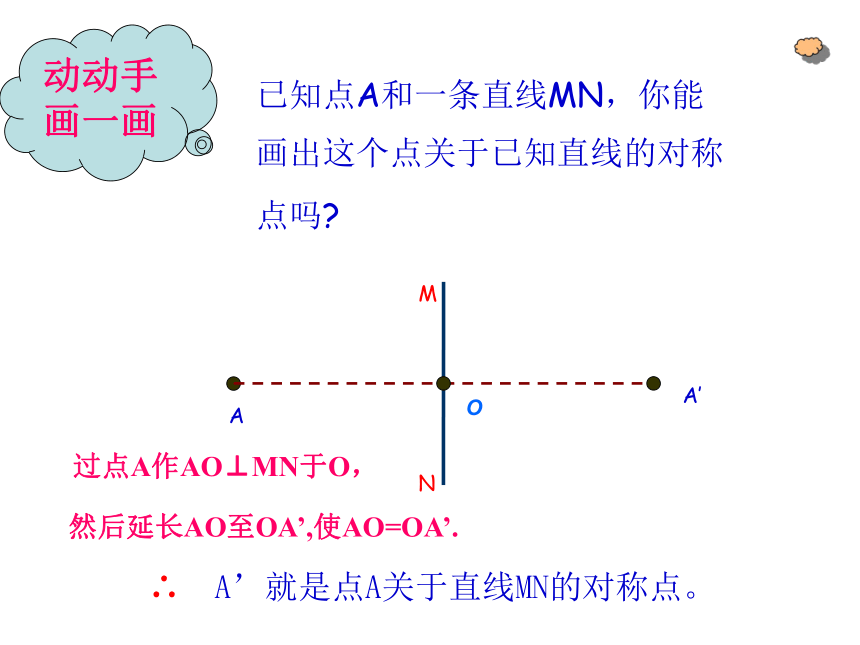
已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗
A
A’
M
N
∴ A’就是点A关于直线MN的对称点。
O
然后延长AO至OA’,使AO=OA’.
过点A作AO⊥MN于O,
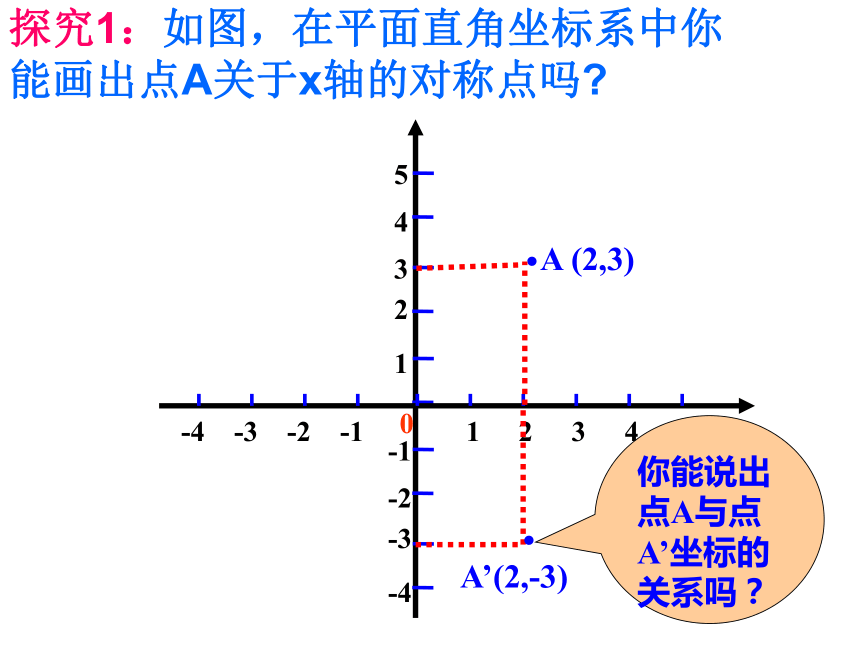
探究1:如图,在平面直角坐标系中你能画出点A关于x轴的对称点吗
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
·
A’(2,-3)
你能说出点A与点A’坐标的关系吗?
在平面直角坐标系中画出下列各点关于x轴的对称点.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B’ (-4, -2)
·
C’(3, 4)
思考:关于x轴对称的点的坐标具有怎样的关系?
归纳:关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
练习:
1、点P(-5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2、点M(a, -5)与点N(-2, b)关于x轴对称,则a=_____, b =_____.
(- 5 , -6 )
-2
5
探究2:如图,你能在平面直角坐标系中画出点A关于y轴的对称点吗
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
·
A’(-2,3)
你能说出点A与点A’坐标的关系吗?
在平面直角坐标系中画出下列各点关于y轴的对称点.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B’ (4, 2)
·
C’(-3, -4)
思考:关于y轴对称的点的坐标具有怎样的关系?
归纳:关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
练习:
1、点P(-5, 6)与点Q关于y轴对称,则点Q的坐标为__________.
2、点M(a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
( 5 , 6 )
2
-5
小结:在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
点(x, y)关于x轴对称的点的坐标为______.
点(x, y)关于y轴对称的点的坐标为______.
(x, - y)
(- x, y)
1、完成下表.
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴的对称点
关于y轴的对称点
(-2, -3)
(2,-3)
(-1,-2)
(1, 2)
(6, -5)
(-6, 5)
(0, -1.6)
(0,1.6)
(-4,0)
(4,0)
2、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
练 习
2
4
6
-20
0
1
2
3
4
5
-4
-3
-2
-1
x
·
·
·
·
A
B
C
D
3
1
4
2
5
-2
-4
-1
-3
y
·
·
A1
B1
D1
C1
·
·
活动一:
1、观察图中两个圆脸有什么关系?
轴对称关系(关于y轴对称)
?
?
2、已知右边圆脸中眼睛A的坐标为(2,3)B的坐标为(4,3)嘴角C的坐标为(4,1)D的坐标为(2,1)。
·
·
·
·
A
B
C
D
·
·
A1
B1
D1
C1
·
·
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
活动二:
3、你能根据轴对称的性质写出左边圆脸的眼睛和嘴角的坐标吗?
(2,3)
(4,3)
(4,1)
(2,1)
·
·
·
·
A
B
C
D
·
·
A1
B1
·
·
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
活动三:
A1的坐标为_________ B1的坐标为________
C1的坐标为_________ D1的坐标为________
(-2,3)
(-4,3)
(-4,1)
(-2,1)
C1
D1
返回
(4,3)
(2,3)
(4,1)
(2,1)
例:已知△ABC的三个顶点的坐标分别为A
(-3,5),B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。
解:点A(-3,5),B(-4,1),
C(-1,3),关于y轴对称
点的坐标分别为A’(3,5), B’(4,1),C’(1,3).依次连接A’B’,B’C’,C’A’,就得到△ABC关于y轴对称的△A’B’C’.
·
·
·
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
c
B
B’
A’
C’
归纳:先求出已知图形中的 特殊点(如多边形的顶点或端点)的对应点的坐标,描出并连接这些点,就可 得到这个图形的轴对称图形.
x
y
5
1
2
1
2
5
5
4
思考:如图,分别作出点P,M,N关于直线x=1(即把y轴向右平移1个长度单位)的对称点, 你能发现它们坐标的关系吗
3
1
4
2
5
-2
-1
0
1
2
3
4
5
-4
-3
-2
-1
x=1
·
·
·
·
·
·
P(-2,4)
M(-1,1)
N’(5,-2)
N(-3,-2)
M’(3,1)
P’(4,4)
15
x
y
,
’
拓展提高
1、学习了在平面直角坐标系中,关于x轴和y轴对称的点的坐标的特点。
这节课你学到了什么?
关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
2、学习了在平面直角坐标系中如何画一个图形关于x轴或y轴的对称图形
先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
用坐标表示轴对称
人教版八年级数学上册(2课时)
由一个平面图形得到它的轴对称图形,这样的变换叫做图形的轴对称变换
——成轴对称的两个图形的任何一个可以看作由另一个图形经过轴对称变换后得到的;
一个轴对称图形也可以看作以它的一部分为基础,经轴对称变换扩展而成的。
应用:已知一个图形和一条直线,你能作出它的轴对称图形吗?
轴对称变换
已知对称轴L和一个点A,你能画出点A关于L的对应点A 吗?
A·
L
·
A
1、过点A作对称轴L的垂线,垂足为B
2、延长AB至A ,使得B A =AB
B
3、点A 就是点A关于直线L的对应点
基础一
1、过点A作对称轴L的垂线A A ,使CA=C A
已知对称轴L和一条线段AB,画出线段AB 关于L的对应线段A B 。
A
B
A
B
L
2、过点A作对称轴L的垂线BB ,使DB=DB
3、连接A B ,线段A B 就是关于直线
L的对应线段
C
D
基础二
成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到。一个轴对称图形也可以看作以它的一部分为基础,经轴对称变换扩展而得到
基础三
如果有一 个图形和一条直线,如何作出与这个通行关于这条直线对称的图形呢?
例: 如图,已知△ABC
和直线L,作出与△ABC 关
于直线L对称的图形
△ 就是所求作的三角形
已知 ABC和直线m,以直线m为对称轴,作 ABC经的对称图形
B
C
A
作法:1、作AP⊥直线m于P,延长AP至Aˊ,使APˊ=AP,则点Aˊ就是点A关于直线m的对称点,同理点B和点C一样作.
2、连结A’B’,B’C’,CˊAˊ
AˊB’C’即为所求
随堂练习
Aˊ
Bˊ
Cˊ
归纳
(1)几何图形都可以看作由点组成,只要作出这些点关于对称轴的对应点,再连接对应点,就可以得到原图形的轴对称图形
(2)对于一些由直线、线段或射线组成的图形只要作出图形中的一些特殊点的对称点,再连接对应点,就可以得到原图形的轴对称图形
动动手画一画
已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗
A
A’
M
N
∴ A’就是点A关于直线MN的对称点。
O
然后延长AO至OA’,使AO=OA’.
过点A作AO⊥MN于O,
探究1:如图,在平面直角坐标系中你能画出点A关于x轴的对称点吗
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
·
A’(2,-3)
你能说出点A与点A’坐标的关系吗?
在平面直角坐标系中画出下列各点关于x轴的对称点.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B’ (-4, -2)
·
C’(3, 4)
思考:关于x轴对称的点的坐标具有怎样的关系?
归纳:关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
练习:
1、点P(-5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2、点M(a, -5)与点N(-2, b)关于x轴对称,则a=_____, b =_____.
(- 5 , -6 )
-2
5
探究2:如图,你能在平面直角坐标系中画出点A关于y轴的对称点吗
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
·
A’(-2,3)
你能说出点A与点A’坐标的关系吗?
在平面直角坐标系中画出下列各点关于y轴的对称点.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B’ (4, 2)
·
C’(-3, -4)
思考:关于y轴对称的点的坐标具有怎样的关系?
归纳:关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
练习:
1、点P(-5, 6)与点Q关于y轴对称,则点Q的坐标为__________.
2、点M(a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
( 5 , 6 )
2
-5
小结:在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
点(x, y)关于x轴对称的点的坐标为______.
点(x, y)关于y轴对称的点的坐标为______.
(x, - y)
(- x, y)
1、完成下表.
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴的对称点
关于y轴的对称点
(-2, -3)
(2,-3)
(-1,-2)
(1, 2)
(6, -5)
(-6, 5)
(0, -1.6)
(0,1.6)
(-4,0)
(4,0)
2、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
练 习
2
4
6
-20
0
1
2
3
4
5
-4
-3
-2
-1
x
·
·
·
·
A
B
C
D
3
1
4
2
5
-2
-4
-1
-3
y
·
·
A1
B1
D1
C1
·
·
活动一:
1、观察图中两个圆脸有什么关系?
轴对称关系(关于y轴对称)
?
?
2、已知右边圆脸中眼睛A的坐标为(2,3)B的坐标为(4,3)嘴角C的坐标为(4,1)D的坐标为(2,1)。
·
·
·
·
A
B
C
D
·
·
A1
B1
D1
C1
·
·
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
活动二:
3、你能根据轴对称的性质写出左边圆脸的眼睛和嘴角的坐标吗?
(2,3)
(4,3)
(4,1)
(2,1)
·
·
·
·
A
B
C
D
·
·
A1
B1
·
·
3
1
4
2
5
-2
-4
-1
-3
y
0
1
2
3
4
5
-4
-3
-2
-1
x
活动三:
A1的坐标为_________ B1的坐标为________
C1的坐标为_________ D1的坐标为________
(-2,3)
(-4,3)
(-4,1)
(-2,1)
C1
D1
返回
(4,3)
(2,3)
(4,1)
(2,1)
例:已知△ABC的三个顶点的坐标分别为A
(-3,5),B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。
解:点A(-3,5),B(-4,1),
C(-1,3),关于y轴对称
点的坐标分别为A’(3,5), B’(4,1),C’(1,3).依次连接A’B’,B’C’,C’A’,就得到△ABC关于y轴对称的△A’B’C’.
·
·
·
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
c
B
B’
A’
C’
归纳:先求出已知图形中的 特殊点(如多边形的顶点或端点)的对应点的坐标,描出并连接这些点,就可 得到这个图形的轴对称图形.
x
y
5
1
2
1
2
5
5
4
思考:如图,分别作出点P,M,N关于直线x=1(即把y轴向右平移1个长度单位)的对称点, 你能发现它们坐标的关系吗
3
1
4
2
5
-2
-1
0
1
2
3
4
5
-4
-3
-2
-1
x=1
·
·
·
·
·
·
P(-2,4)
M(-1,1)
N’(5,-2)
N(-3,-2)
M’(3,1)
P’(4,4)
15
x
y
,
’
拓展提高
1、学习了在平面直角坐标系中,关于x轴和y轴对称的点的坐标的特点。
这节课你学到了什么?
关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
2、学习了在平面直角坐标系中如何画一个图形关于x轴或y轴的对称图形
先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
