第十八章 平行四边形 单元同步测试卷(四)(含答案)
文档属性
| 名称 | 第十八章 平行四边形 单元同步测试卷(四)(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十八章
平行四边形单元测试卷
题号
一
二
三
总分
17
18
19
20
21
22
分数
一.选择题(每题3分,共30分)
1.下列四个命题中,假命题是(
)
A.对角线互相平分的四边形是平行四边形
B.对角线互相垂直平分的四边形是矩形
C.对角线互相垂直的平行四边形是菱形
D.对角线互相垂直且相等的平行四边形是正方形
2.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8.BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2
B.
C.3
D.4
3.如图,在矩形中,对角线、相交于点O,若,,则=(
)
A.18°
B.36°
C.27°
D.54°
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
8.如图5,E,F分别是?ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到四边形EFC′D′,ED′交BC于点G,则△GEF的周长为( )
图5
A.6
B.12
C.18
D.24
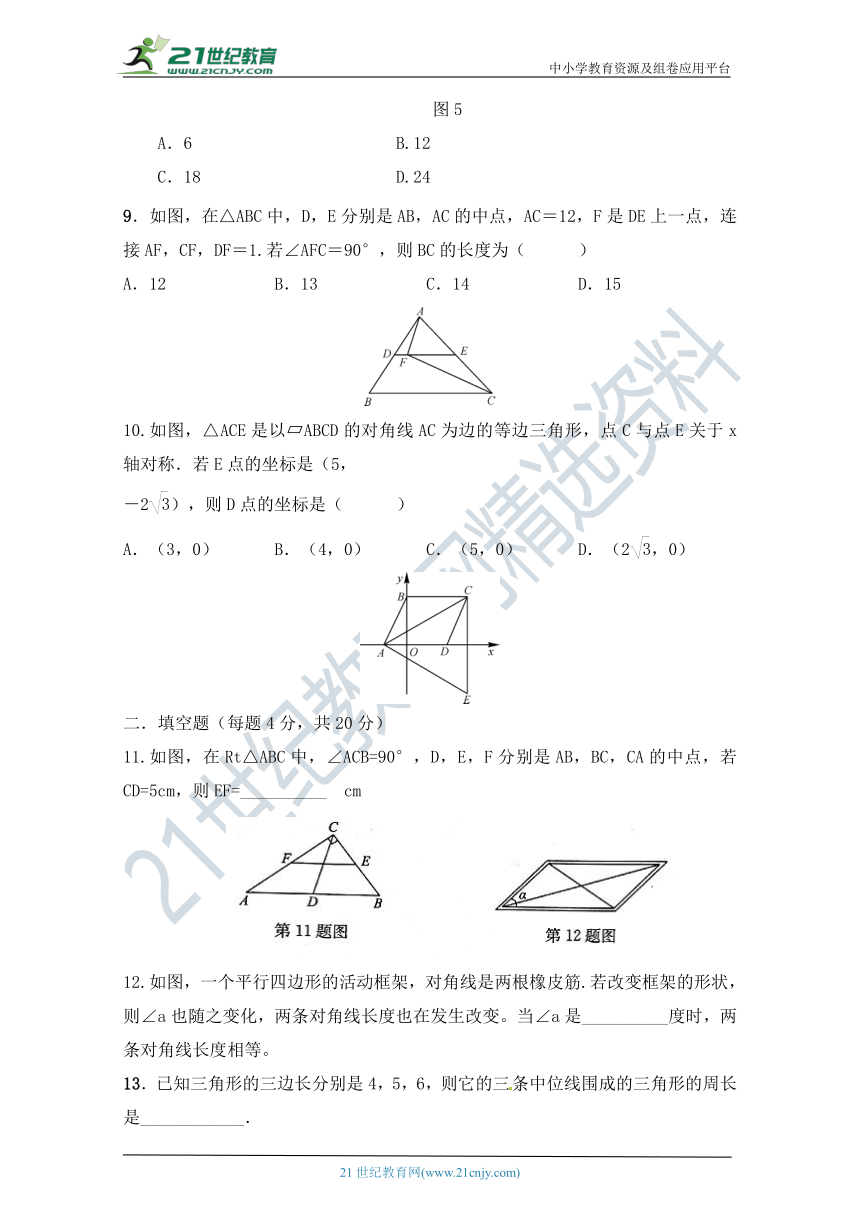
9.如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为(
)
A.12
B.13
C.14
D.15
10.如图,△ACE是以?ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(5,
-2),则D点的坐标是(
)
A.(3,0)
B.(4,0)
C.(5,0)
D.(2,0)
二.填空题(每题4分,共20分)
11.如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,BC,CA的中点,若CD=5cm,则EF=__________?cm
12.如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠a也随之变化,两条对角线长度也在发生改变。当∠a是__________度时,两条对角线长度相等。
13.已知三角形的三边长分别是4,5,6,则它的三条中位线围成的三角形的周长是____________.
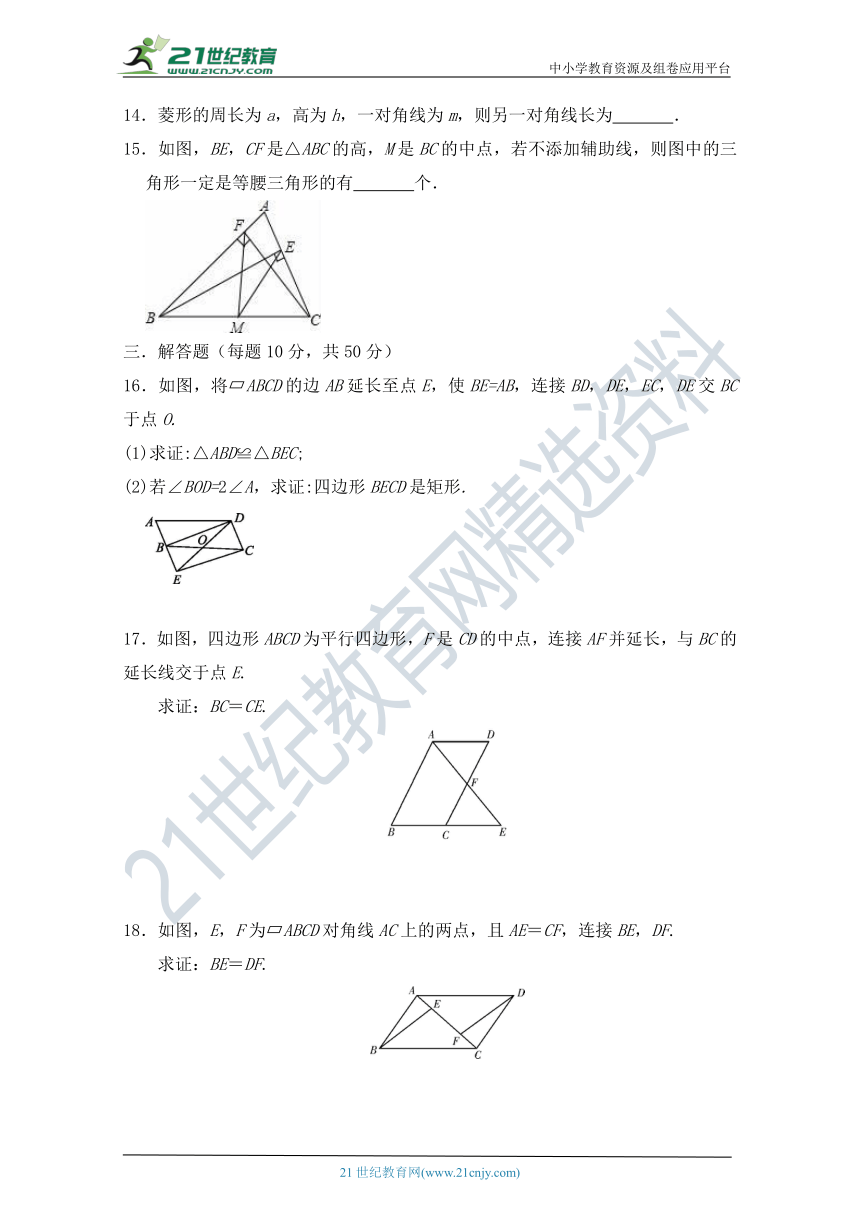
14.菱形的周长为a,高为h,一对角线为m,则另一对角线长为
.
15.如图,BE,CF是△ABC的高,M是BC的中点,若不添加辅助线,则图中的三角形一定是等腰三角形的有
个.
三.解答题(每题10分,共50分)
16.如图,将?ABCD的边AB延长至点E,使BE=AB,连接BD,DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
17.如图,四边形ABCD为平行四边形,F是CD的中点,连接AF并延长,与BC的延长线交于点E.
求证:BC=CE.
18.如图,E,F为?ABCD对角线AC上的两点,且AE=CF,连接BE,DF.
求证:BE=DF.
19.如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于点E.
(1)求证:△AFE≌△CDE;
(2)若AB=4,BC=8,求图中阴影部分的面积.
20.如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,经通过平移得到的线段记为PQ,连接PA,QD,并过点Q作QO⊥BD,垂足为O,连接OA,OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA,OP之间的数量关系和位置关系,并加以证明.
参考答案
一.选择题
1.
B
2.
B.
3.
A.
4.
C.
5.
D.
6.
C.
7.
C.
8.
C.
9.
C.
10.B
二.填空题(共5小题)
11.5
12.90
13.7.5
14.解:∵菱形的周长为a,
∴菱形的边长为,
设另一对角线长为x,
则菱形的面积=xm=?h,
解得x=.
故答案为:.
15.解:∵BE是△ABC的高,
∴BE⊥CE.
又点M是BC的中点,
∴在Rt△BCE中,
ME=BM=CM(直角三角形斜边上的中线等于斜边的一半),
∴△BME、△CME是等腰三角形;
同理,△BMF、△CMF是等腰三角形.
综上所述△BME、△CME、△BMF、△CMF都是等腰三角形;
故答案是:4.
三.解答题(共5小题)
16.【答案】
[解析](1)根据平行四边形的判定与性质得到四边形BECD为平行四边形,然后由SSS推出两三角形全等即可;(2)欲证明四边形BECD是矩形,只需推出BC=ED即可.
证明:(1)在?ABCD中,AD=BC,AB=CD,AB∥CD,则BE∥CD.
又∵BE=AB,∴BE=DC,
∴四边形BECD是平行四边形,
∴BD=EC.
在△ABD与△BEC中,
∴△ABD≌△BEC(SSS).
(2)由(1)知四边形BECD是平行四边形,
则OD=OE,OC=OB.
∵四边形ABCD是平行四边形,
∴∠A=∠BCD,即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC,
∴OC=OD,
∴BC=ED,
∴平行四边形BECD是矩形.
17.略
18.略
19.(1)略 (2)S阴影=10
20.解:(1)四边形APQD是平行四边形.(2)OA⊥OP,OA=OP.∵四边形ABCD为正方形,∴∠ABO=∠OBC=45°.∵OQ⊥BD,∴∠BOQ=90°.∴∠OQB=45°.∴∠OQB=∠ABO=∠OBQ=45°.∴OB=OQ.在△ABO和△PQO中,∴△ABO≌△PQO(SAS).∴OA=OP,∠AOB=∠POQ.∵∠BOQ=∠BOP+∠POQ=90°,∴∠BOP+∠AOB=∠AOP=90°.∴OA⊥OP.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第十八章
平行四边形单元测试卷
题号
一
二
三
总分
17
18
19
20
21
22
分数
一.选择题(每题3分,共30分)
1.下列四个命题中,假命题是(
)
A.对角线互相平分的四边形是平行四边形
B.对角线互相垂直平分的四边形是矩形
C.对角线互相垂直的平行四边形是菱形
D.对角线互相垂直且相等的平行四边形是正方形
2.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8.BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2
B.
C.3
D.4
3.如图,在矩形中,对角线、相交于点O,若,,则=(
)
A.18°
B.36°
C.27°
D.54°
4.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
5.如图,正方形ABCD中,DE=2AE=4,F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为( )
A.
B.5
C.
D.2
6.如图,菱形ABCD中,∠B=120°,则∠1的度数是( )
A.30°
B.25°
C.20°
D.15°
7.如图,在?ABCD中,AC,BD为对角线,BC=10,BC边上的高为6,则图中阴影部分的面积为( )
A.6
B.15
C.30
D.60
8.如图5,E,F分别是?ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到四边形EFC′D′,ED′交BC于点G,则△GEF的周长为( )
图5
A.6
B.12
C.18
D.24
9.如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为(
)
A.12
B.13
C.14
D.15
10.如图,△ACE是以?ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(5,
-2),则D点的坐标是(
)
A.(3,0)
B.(4,0)
C.(5,0)
D.(2,0)
二.填空题(每题4分,共20分)
11.如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,BC,CA的中点,若CD=5cm,则EF=__________?cm
12.如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠a也随之变化,两条对角线长度也在发生改变。当∠a是__________度时,两条对角线长度相等。
13.已知三角形的三边长分别是4,5,6,则它的三条中位线围成的三角形的周长是____________.
14.菱形的周长为a,高为h,一对角线为m,则另一对角线长为
.
15.如图,BE,CF是△ABC的高,M是BC的中点,若不添加辅助线,则图中的三角形一定是等腰三角形的有
个.
三.解答题(每题10分,共50分)
16.如图,将?ABCD的边AB延长至点E,使BE=AB,连接BD,DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
17.如图,四边形ABCD为平行四边形,F是CD的中点,连接AF并延长,与BC的延长线交于点E.
求证:BC=CE.
18.如图,E,F为?ABCD对角线AC上的两点,且AE=CF,连接BE,DF.
求证:BE=DF.
19.如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于点E.
(1)求证:△AFE≌△CDE;
(2)若AB=4,BC=8,求图中阴影部分的面积.
20.如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,经通过平移得到的线段记为PQ,连接PA,QD,并过点Q作QO⊥BD,垂足为O,连接OA,OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA,OP之间的数量关系和位置关系,并加以证明.
参考答案
一.选择题
1.
B
2.
B.
3.
A.
4.
C.
5.
D.
6.
C.
7.
C.
8.
C.
9.
C.
10.B
二.填空题(共5小题)
11.5
12.90
13.7.5
14.解:∵菱形的周长为a,
∴菱形的边长为,
设另一对角线长为x,
则菱形的面积=xm=?h,
解得x=.
故答案为:.
15.解:∵BE是△ABC的高,
∴BE⊥CE.
又点M是BC的中点,
∴在Rt△BCE中,
ME=BM=CM(直角三角形斜边上的中线等于斜边的一半),
∴△BME、△CME是等腰三角形;
同理,△BMF、△CMF是等腰三角形.
综上所述△BME、△CME、△BMF、△CMF都是等腰三角形;
故答案是:4.
三.解答题(共5小题)
16.【答案】
[解析](1)根据平行四边形的判定与性质得到四边形BECD为平行四边形,然后由SSS推出两三角形全等即可;(2)欲证明四边形BECD是矩形,只需推出BC=ED即可.
证明:(1)在?ABCD中,AD=BC,AB=CD,AB∥CD,则BE∥CD.
又∵BE=AB,∴BE=DC,
∴四边形BECD是平行四边形,
∴BD=EC.
在△ABD与△BEC中,
∴△ABD≌△BEC(SSS).
(2)由(1)知四边形BECD是平行四边形,
则OD=OE,OC=OB.
∵四边形ABCD是平行四边形,
∴∠A=∠BCD,即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC,
∴OC=OD,
∴BC=ED,
∴平行四边形BECD是矩形.
17.略
18.略
19.(1)略 (2)S阴影=10
20.解:(1)四边形APQD是平行四边形.(2)OA⊥OP,OA=OP.∵四边形ABCD为正方形,∴∠ABO=∠OBC=45°.∵OQ⊥BD,∴∠BOQ=90°.∴∠OQB=45°.∴∠OQB=∠ABO=∠OBQ=45°.∴OB=OQ.在△ABO和△PQO中,∴△ABO≌△PQO(SAS).∴OA=OP,∠AOB=∠POQ.∵∠BOQ=∠BOP+∠POQ=90°,∴∠BOP+∠AOB=∠AOP=90°.∴OA⊥OP.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
