山东省菏泽市某重点中学2011-2012学年度下学期高三2月月考数学试题(理)
文档属性
| 名称 | 山东省菏泽市某重点中学2011-2012学年度下学期高三2月月考数学试题(理) | 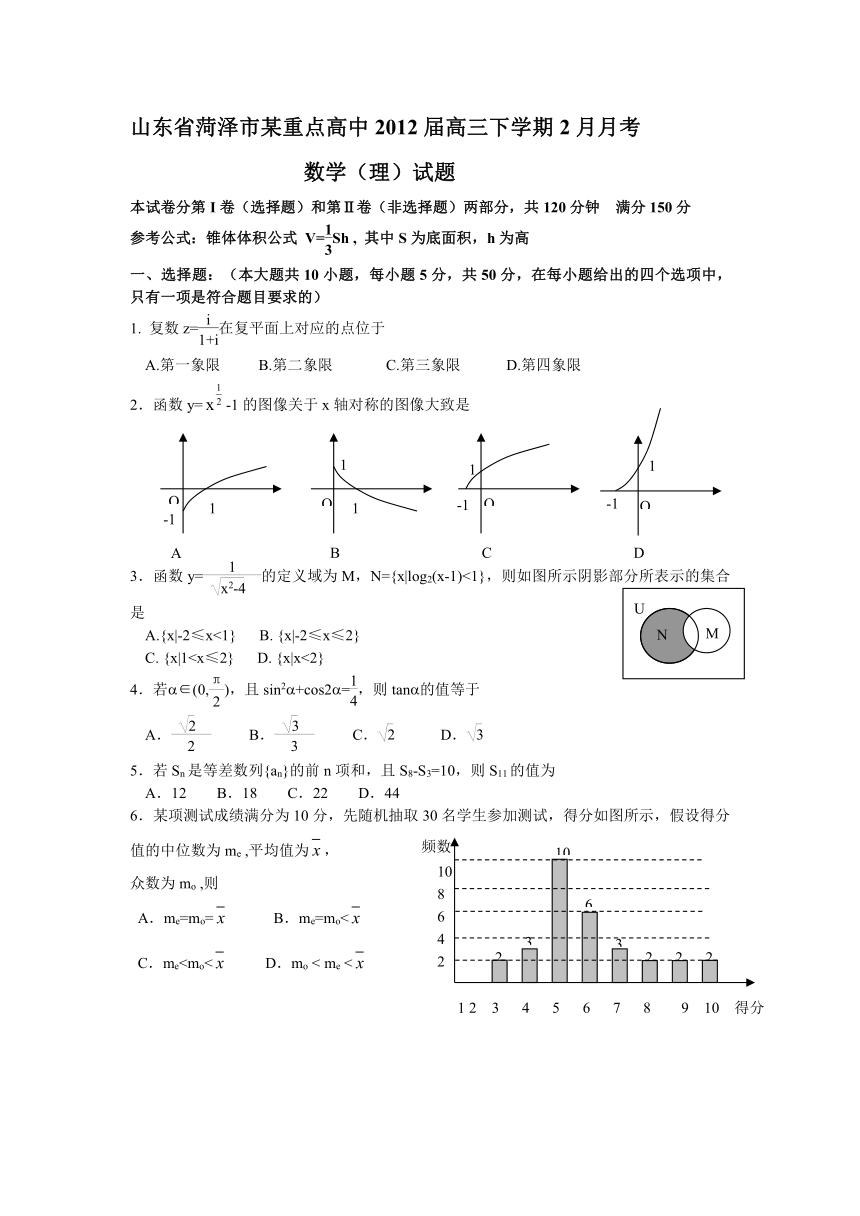 | |
| 格式 | zip | ||
| 文件大小 | 188.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-05 09:05:45 | ||
图片预览




文档简介
山东省菏泽市某重点高中2012届高三下学期2月月考
数学(理)试题
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共120分钟 满分150分
参考公式:锥体体积公式 V=Sh , 其中S为底面积,h为高
一、选择题:(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 复数z=在复平面上对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.函数y=-1的图像关于x轴对称的图像大致是
3.函数y= EQ \f( 1 , )的定义域为M,N={x|log2(x-1)<1},则如图所示阴影部分所表示的集合是
A.{x|-2≤x<1} B. {x|-2≤x≤2}
C. {x|14.若∈(0,),且sin2+cos2=,则tan的值等于
A. EQ \f( , 2 ) B. EQ \f( , 3 ) C. D.
5.若Sn是等差数列{an}的前n项和,且S8-S3=10,则S11的值为
A.12 B.18 C.22 D.44
6.某项测试成绩满分为10分,先随机抽取30名学生参加测试,得分如图所示,假设得分值的中位数为me ,平均值为,
众数为mo ,则
A.me=mo= B.me=mo<
C.me7.程序框图,如图所示,
已知曲线E的方程为ax2+by2=ab (a,b∈R),若该程序输出的结果为s,则
A.当s=1时,E是椭圆 B.当s= -1时,E是双曲线
C.当s=0时,E是抛物线 D.当s=0时,E是一个点
8.已知a、b、c是三条不同的直线,命题“a∥b且a⊥cb⊥c”是正确的,如果把a、b、c中的两个或三个换成平面,在所得的命题中,真命题有
A.1个 B.2个 C.3个 D.4个
9.已知函数f(x)=|log(x-1)|- ()x有两个零点x1,x2,则有
A.x1x2<1 B.x1x2x1+x2
10.已知△ABC外接圆半径R= EQ \f( 14 , 3 ),且∠ABC=120°,BC=10,边BC在轴x上且y轴垂直平分BC边,则过点A且以B,C为焦点的双曲线方程为
A. — =1 B. — =1 C. — =1 D . — =1
第Ⅱ卷
二 、填空题:(本大题共5小题,每小题5分,共25分)
11.若“x2-2x-8>0”是“x12.设n=,则二项式(x-)n的展开式中,x2项的系数为
13.已知关于x的方程x2+2px-(q2-2)=0 (p、q∈R)无实根,则p+q的取值范围是
14.在区间[-6,6]内任取一个元素x0 ,抛物线x2=4y在x=x0处的切线的倾斜角为,则∈[,],
的概率为
三.选做题:清考生在下列两题中任选一题作答,若两题都做,则按做的第一题评阅计分。本题共5分。
15.(1)(不等式选讲选做题)若关于x的不等式|x-1|+|x+m|>3的解集为R,则实数m的取值范围是
(2) (坐标系与参数方程选做题)已知抛物线C1的参数方程为 (t为参数),圆C2的极坐标方程为=r (r>0),若斜率为1的直线经过抛物线C1的焦点,且与圆C2相切,则r=
三、解答题:(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤)
16.(本小题满分12分) 已知向量 EQ \o \ac (,p)=(-cos2x,a), EQ \o \ac (,q)=(a, 2-sin2x),函数f(x)= EQ \o \ac (,p)· EQ \o \ac (,q)-5(a∈R,a≠0) (1)求函数f(x) (x∈R)的值域;
(2)当a=2时,若对任意的t∈R,函数y=f(x),x∈(t,t+b]的图像与直线y=-1有且仅有两个不同的交点,试确定b的值,(不必证明),并求函数y=f(x)在[0,b]上的单调递增区间。
17.(本小题满分12分)
已知各项均不相等的等差数列{an}的前四项和S4=14,且a1,a3,a7成等比数列.
(1)求数列{an}的通项公式;
(2)设Tn为数列{}的前n项和,若Tn≤an+1对n∈N*恒成立,求实数的最小值
18.(本小题满分12分)南昌教育局组织中学生足球比赛,共有实力相当的8支代表队(含有一中代表队,二中代表队)参加比赛,比赛规则如下:第一轮:抽签分成四组,每组两队进行比赛,胜队进入第二轮。第二轮:将四队分成两组,每组两队进行比赛,胜队进入第三轮。第三轮:两队进行决赛,胜队获得冠军。
现记ξ=0表示整个比赛中一中代表队与二中代表队没有相遇,ξ=i表示恰好在第i轮比赛时一中代表队,二中代表队相遇(i=1,2,3).
求ξ的分布列;
求Eξ
(19) (本小题满分12分)
如图,已知E,F分别是正方形ABCD边BC,CD的中点,EF与AC交于点O, PA,NC都垂直于平面ABCD,且PA=AB=4,NC=2, M是线段PA上一动点
求证:平面PAC⊥平面NEF;
若PC∥平面MEF,试求PM∶MA的值;
当M是PA中点时,求二面角M-EF-N的余弦值
20.(本小题满分13分)
椭圆E的中心在坐标原点O,焦点在x轴上,离心率为,点P(1,),A,B在椭圆E上,且
EQ \o \ac (,PA)+ EQ \o \ac (,PB)=m EQ \o \ac (,OP) (m∈R)
求椭圆E的方程及直线AB的斜率;
求证:当△PAB的面积取得最大值时,原点O是△PAB的重心
21.(本小题满分14分)
已知函数f(x)= (m,n∈R)在x=1处取到极值2 .
求f(x)的解析式;
设函数g(x)=ax-lnx .若对任意的x1∈[,2],总存在唯一的x2∈[,e] (e为自然对数的底),使得g(x2)= f(x1) ,求实数a的取值范围。
山东省菏泽市某重点高中2012届高三下学期2月月考
数学(理科)参考答案及评分标准
一、选择题(本大题共10题,每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C D C D B C B A
二、填空题(本大题共4小题,每小题5分,共20分)
11. 12.60 13. 14.
三、选做题(本题共5分)
15.①; ②
四、解答题(本大题共6小题,共75分)
16. 解:(1)
………………………………………………………2分
因为,所以
当时,
所以的值域为………………………………………………………4分
同理,当时,的值域为 ……………………………………6分
(2)当时,
的最小正周期为可知,的值为.…………………8分
由,得……10分
因为,所以,
函数在上的单调递增区间为………………………………12分
17. 解:(1)设公差为。由已知得………………………3分
解得或 (舍去) 所以,故 ………………………………6分
(2)因为
所以………………………9分
因为对恒成立。即,,对恒成立。
又
所以实数的最小值为 ………………………………………………………………12分
18. 解:(1) ……………………………………….2分
……………………………………4分
…………………………………………………….6分
……………………………….9分
(2)………………………………………….12分
19. 解:法1:(1)连结,
∵平面,平面,
∴,……………………… 1分
又∵,,
∴平面,…………………. 2分
又∵,分别是、的中点,
∴,………………………….3分
∴平面,又平面,
∴平面平面;……………4分
(2)连结,
∵平面,平面平面,
∴,
∴,故 ………………………………………8分
(3)∵平面,平面,∴,
在等腰三角形中,点为的中点,∴,
∴为所求二面角的平面角, ……………………………9分
∵点是的中点,∴,
所以在矩形中,
可求得,,,………………………10分
在中,由余弦定理可求得,
∴二面角的余弦值为.……………………………………12分
法2:(1)同法1;
(2)建立如图所示的直角坐标系,则,,,,
∴,,
设点的坐标为,平面的法向量为,则,
所以,即,令,则,,
故,
∵平面,∴,即,解得,
故,即点为线段上靠近的四等分点;
故 …………………………………………………………………8分
(3),则,设平面的法向量为,
则,即,………9分
令,则,,
即,……………………………10分
当是中点时,,
则,
∴,
∴二面角的余弦值为.……12分
20. 解:(1)由=及解得a2=4,b2=3,
椭圆方程为;…………………………………………………………2分
设A(x1,y1)、B(x2,y2), 由得
(x1+x2-2,y1+y2-3)=m(1,),即
又,,两式相减得
; ………………………6分
(2)设AB的方程为 y=,代入椭圆方程得:x2-tx+t2-3=0,
△=3(4-t2),|AB|=,
点P到直线AB的距离为d=,
S△PAB == (-2令f(t) =3(2-t)3(2+t),则f’(t)=-12(2-t)2(t+1),由f’(t)=0得t=-1或2(舍),
当-20,当-1即△PAB的面积的最大值是;
根据韦达定理得 x1+x2=t=-1,而x1+x2=2+m,所以2+m=-1,得m=-3,
于是x1+x2+1=3+m=0,y1+y2+=3++=0,
因此△PAB的重心坐标为(0,0).……………………………………………………13分
21. 解: (1) …………………………2分
由在处取到极值2,故,即,
解得,经检验,此时在处取得极值.故 ……5分
(2)由(1)知,故在上单调递增,在上单调递减,由 ,故的值域为…………………………7分
依题意,记
(ⅰ)当时,,在上单调递减,
依题意由,得,……………………………………………………8分
(ⅱ)当时,当时,,当时,
依题意得:或,解得,…………………………10分
(ⅲ)当时,,此时,在上单调递增依题意得
即此不等式组无解 ……………………………………11分.
综上,所求取值范围为………………………………………………14分
1
-1
O
A
1
O
1
B
1
O
-1
C
1
O
-1
D
N
M
U
1 2 3 4 5 6 7 8 9 10 得分
10
8
6
4
2
2
2
2
2
3
6
10
频数
3
输出0
开始
输入a,b
c=ab
c=0
c=0
输出1
输出-1
结束
否
是
是
否
P
O
F
E
D
C
B
A
N
M
数学(理)试题
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共120分钟 满分150分
参考公式:锥体体积公式 V=Sh , 其中S为底面积,h为高
一、选择题:(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 复数z=在复平面上对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.函数y=-1的图像关于x轴对称的图像大致是
3.函数y= EQ \f( 1 , )的定义域为M,N={x|log2(x-1)<1},则如图所示阴影部分所表示的集合是
A.{x|-2≤x<1} B. {x|-2≤x≤2}
C. {x|1
A. EQ \f( , 2 ) B. EQ \f( , 3 ) C. D.
5.若Sn是等差数列{an}的前n项和,且S8-S3=10,则S11的值为
A.12 B.18 C.22 D.44
6.某项测试成绩满分为10分,先随机抽取30名学生参加测试,得分如图所示,假设得分值的中位数为me ,平均值为,
众数为mo ,则
A.me=mo= B.me=mo<
C.me
已知曲线E的方程为ax2+by2=ab (a,b∈R),若该程序输出的结果为s,则
A.当s=1时,E是椭圆 B.当s= -1时,E是双曲线
C.当s=0时,E是抛物线 D.当s=0时,E是一个点
8.已知a、b、c是三条不同的直线,命题“a∥b且a⊥cb⊥c”是正确的,如果把a、b、c中的两个或三个换成平面,在所得的命题中,真命题有
A.1个 B.2个 C.3个 D.4个
9.已知函数f(x)=|log(x-1)|- ()x有两个零点x1,x2,则有
A.x1x2<1 B.x1x2
10.已知△ABC外接圆半径R= EQ \f( 14 , 3 ),且∠ABC=120°,BC=10,边BC在轴x上且y轴垂直平分BC边,则过点A且以B,C为焦点的双曲线方程为
A. — =1 B. — =1 C. — =1 D . — =1
第Ⅱ卷
二 、填空题:(本大题共5小题,每小题5分,共25分)
11.若“x2-2x-8>0”是“x
13.已知关于x的方程x2+2px-(q2-2)=0 (p、q∈R)无实根,则p+q的取值范围是
14.在区间[-6,6]内任取一个元素x0 ,抛物线x2=4y在x=x0处的切线的倾斜角为,则∈[,],
的概率为
三.选做题:清考生在下列两题中任选一题作答,若两题都做,则按做的第一题评阅计分。本题共5分。
15.(1)(不等式选讲选做题)若关于x的不等式|x-1|+|x+m|>3的解集为R,则实数m的取值范围是
(2) (坐标系与参数方程选做题)已知抛物线C1的参数方程为 (t为参数),圆C2的极坐标方程为=r (r>0),若斜率为1的直线经过抛物线C1的焦点,且与圆C2相切,则r=
三、解答题:(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤)
16.(本小题满分12分) 已知向量 EQ \o \ac (,p)=(-cos2x,a), EQ \o \ac (,q)=(a, 2-sin2x),函数f(x)= EQ \o \ac (,p)· EQ \o \ac (,q)-5(a∈R,a≠0) (1)求函数f(x) (x∈R)的值域;
(2)当a=2时,若对任意的t∈R,函数y=f(x),x∈(t,t+b]的图像与直线y=-1有且仅有两个不同的交点,试确定b的值,(不必证明),并求函数y=f(x)在[0,b]上的单调递增区间。
17.(本小题满分12分)
已知各项均不相等的等差数列{an}的前四项和S4=14,且a1,a3,a7成等比数列.
(1)求数列{an}的通项公式;
(2)设Tn为数列{}的前n项和,若Tn≤an+1对n∈N*恒成立,求实数的最小值
18.(本小题满分12分)南昌教育局组织中学生足球比赛,共有实力相当的8支代表队(含有一中代表队,二中代表队)参加比赛,比赛规则如下:第一轮:抽签分成四组,每组两队进行比赛,胜队进入第二轮。第二轮:将四队分成两组,每组两队进行比赛,胜队进入第三轮。第三轮:两队进行决赛,胜队获得冠军。
现记ξ=0表示整个比赛中一中代表队与二中代表队没有相遇,ξ=i表示恰好在第i轮比赛时一中代表队,二中代表队相遇(i=1,2,3).
求ξ的分布列;
求Eξ
(19) (本小题满分12分)
如图,已知E,F分别是正方形ABCD边BC,CD的中点,EF与AC交于点O, PA,NC都垂直于平面ABCD,且PA=AB=4,NC=2, M是线段PA上一动点
求证:平面PAC⊥平面NEF;
若PC∥平面MEF,试求PM∶MA的值;
当M是PA中点时,求二面角M-EF-N的余弦值
20.(本小题满分13分)
椭圆E的中心在坐标原点O,焦点在x轴上,离心率为,点P(1,),A,B在椭圆E上,且
EQ \o \ac (,PA)+ EQ \o \ac (,PB)=m EQ \o \ac (,OP) (m∈R)
求椭圆E的方程及直线AB的斜率;
求证:当△PAB的面积取得最大值时,原点O是△PAB的重心
21.(本小题满分14分)
已知函数f(x)= (m,n∈R)在x=1处取到极值2 .
求f(x)的解析式;
设函数g(x)=ax-lnx .若对任意的x1∈[,2],总存在唯一的x2∈[,e] (e为自然对数的底),使得g(x2)= f(x1) ,求实数a的取值范围。
山东省菏泽市某重点高中2012届高三下学期2月月考
数学(理科)参考答案及评分标准
一、选择题(本大题共10题,每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C D C D B C B A
二、填空题(本大题共4小题,每小题5分,共20分)
11. 12.60 13. 14.
三、选做题(本题共5分)
15.①; ②
四、解答题(本大题共6小题,共75分)
16. 解:(1)
………………………………………………………2分
因为,所以
当时,
所以的值域为………………………………………………………4分
同理,当时,的值域为 ……………………………………6分
(2)当时,
的最小正周期为可知,的值为.…………………8分
由,得……10分
因为,所以,
函数在上的单调递增区间为………………………………12分
17. 解:(1)设公差为。由已知得………………………3分
解得或 (舍去) 所以,故 ………………………………6分
(2)因为
所以………………………9分
因为对恒成立。即,,对恒成立。
又
所以实数的最小值为 ………………………………………………………………12分
18. 解:(1) ……………………………………….2分
……………………………………4分
…………………………………………………….6分
……………………………….9分
(2)………………………………………….12分
19. 解:法1:(1)连结,
∵平面,平面,
∴,……………………… 1分
又∵,,
∴平面,…………………. 2分
又∵,分别是、的中点,
∴,………………………….3分
∴平面,又平面,
∴平面平面;……………4分
(2)连结,
∵平面,平面平面,
∴,
∴,故 ………………………………………8分
(3)∵平面,平面,∴,
在等腰三角形中,点为的中点,∴,
∴为所求二面角的平面角, ……………………………9分
∵点是的中点,∴,
所以在矩形中,
可求得,,,………………………10分
在中,由余弦定理可求得,
∴二面角的余弦值为.……………………………………12分
法2:(1)同法1;
(2)建立如图所示的直角坐标系,则,,,,
∴,,
设点的坐标为,平面的法向量为,则,
所以,即,令,则,,
故,
∵平面,∴,即,解得,
故,即点为线段上靠近的四等分点;
故 …………………………………………………………………8分
(3),则,设平面的法向量为,
则,即,………9分
令,则,,
即,……………………………10分
当是中点时,,
则,
∴,
∴二面角的余弦值为.……12分
20. 解:(1)由=及解得a2=4,b2=3,
椭圆方程为;…………………………………………………………2分
设A(x1,y1)、B(x2,y2), 由得
(x1+x2-2,y1+y2-3)=m(1,),即
又,,两式相减得
; ………………………6分
(2)设AB的方程为 y=,代入椭圆方程得:x2-tx+t2-3=0,
△=3(4-t2),|AB|=,
点P到直线AB的距离为d=,
S△PAB == (-2
当-2
根据韦达定理得 x1+x2=t=-1,而x1+x2=2+m,所以2+m=-1,得m=-3,
于是x1+x2+1=3+m=0,y1+y2+=3++=0,
因此△PAB的重心坐标为(0,0).……………………………………………………13分
21. 解: (1) …………………………2分
由在处取到极值2,故,即,
解得,经检验,此时在处取得极值.故 ……5分
(2)由(1)知,故在上单调递增,在上单调递减,由 ,故的值域为…………………………7分
依题意,记
(ⅰ)当时,,在上单调递减,
依题意由,得,……………………………………………………8分
(ⅱ)当时,当时,,当时,
依题意得:或,解得,…………………………10分
(ⅲ)当时,,此时,在上单调递增依题意得
即此不等式组无解 ……………………………………11分.
综上,所求取值范围为………………………………………………14分
1
-1
O
A
1
O
1
B
1
O
-1
C
1
O
-1
D
N
M
U
1 2 3 4 5 6 7 8 9 10 得分
10
8
6
4
2
2
2
2
2
3
6
10
频数
3
输出0
开始
输入a,b
c=ab
c=0
c=0
输出1
输出-1
结束
否
是
是
否
P
O
F
E
D
C
B
A
N
M
同课章节目录
