10.1随机事件与概率-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(机构适用)(20张PPT)
文档属性
| 名称 | 10.1随机事件与概率-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(机构适用)(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 498.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 17:08:02 | ||
图片预览






文档简介
第十章概率
10.1随机事件与概率
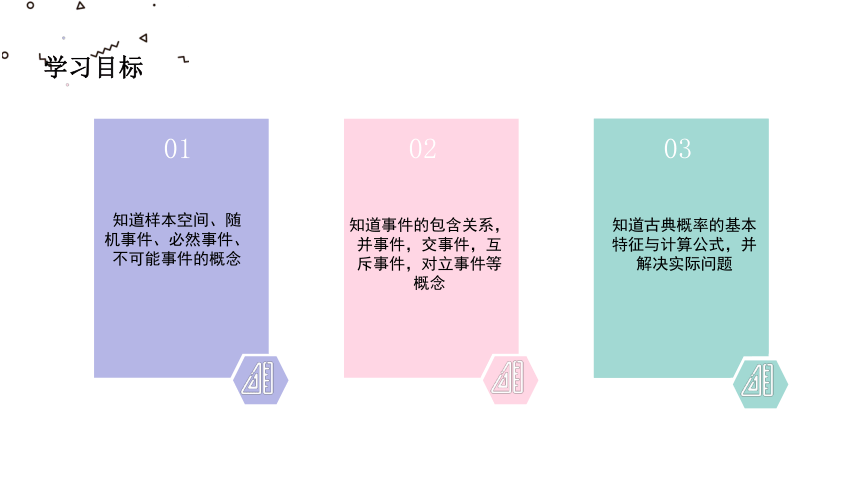
知道样本空间、随机事件、必然事件、不可能事件的概念
01
知道事件的包含关系,并事件,交事件,互斥事件,对立事件等概念
02
知道古典概率的基本特征与计算公式,并解决实际问题
03
学习目标
有限样本空间与随机事件
01
02
03
01
随机试验
我们把对随机现象的实现和对它的观察称为随机试验,简称试验,常用字母E表示.例如,抛一枚硬币、掷一个均匀的骰子等,都可以看成随机试验.
有限样本空间与随机事件
02
02
03
01
样本点和样本空间
(1)定义:我们把随机试验E的每个可能的基本结果称为样本点,全体样本点的集合称为试验E的样本空间
(2)表示:一般地,我们用 表示样本空间,用 表示样本点
(3)有限样本空间:如果一个随机试验有n个可能结果 ,则称样本空间 = 为有限样本空间
有限样本空间与随机事件
02
02
03
01
事件
(1)随机事件:我们将样本空间 的子集称为随机事件,简称事件,并把只包含一个样本点的事件称为基本事件.随机事件一般用大写字母A,B,C,表示,在每次试验中,当且仅当A中某个样本点出现时,称为事件A发生.
(2)必然事件: 作为自身的子集,包含了所有的样本点,在每次试验中总有一个样本点发生,所以 总会发生,我们称 为必然事件.
(3)不可能事件:空集 中不包含任何样本点,在每次试验中都不会发生,我们称 为不可能事件.
有限样本空间与随机事件
02
02
03
01
“守株待兔”是随机事件
“太阳的东升西落”是必然事件
“水中捞月”是不可能事件
事件的关系和运算
02
02
03
02
{5940675A-B579-460E-94D1-54222C63F5DA}
含义
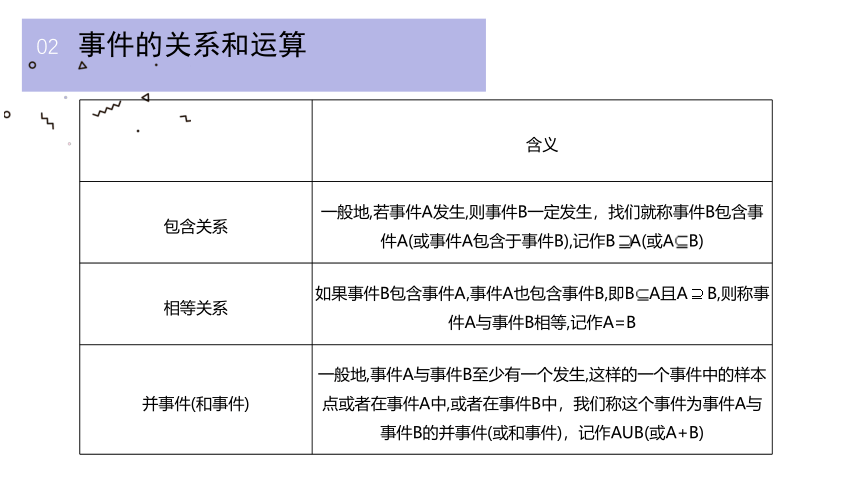
包含关系
一般地,若事件A发生,则事件B一定发生,找们就称事件B包含事件A(或事件A包含于事件B),记作B A(或A B)
相等关系
如果事件B包含事件A,事件A也包含事件B,即B A且A B,则称事件A与事件B相等,记作A=B
并事件(和事件)
一般地,事件A与事件B至少有一个发生,这样的一个事件中的样本点或者在事件A中,或者在事件B中,我们称这个事件为事件A与事件B的并事件(或和事件),记作AUB(或A+B)
事件的关系和运算
02
02
03
02
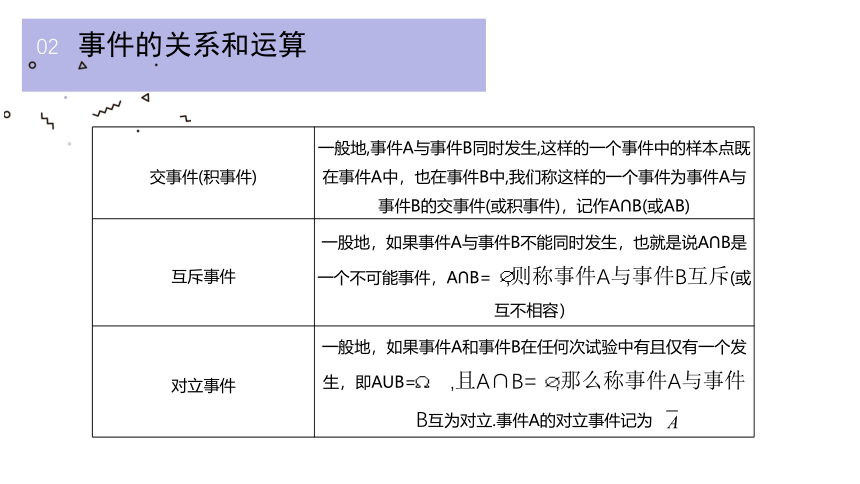
{5940675A-B579-460E-94D1-54222C63F5DA}交事件(积事件)
一般地,事件A与事件B同时发生,这样的一个事件中的样本点既在事件A中,也在事件B中,我们称这样的一个事件为事件A与事件B的交事件(或积事件),记作A∩B(或AB)
互斥事件
一股地,如果事件A与事件B不能同时发生,也就是说A∩B是一个不可能事件,A∩B= ,则称事件A与事件B互斥(或互不相容)
对立事件
一般地,如果事件A和事件B在任何次试验中有且仅有一个发生,即AUB= ,且A∩B= ,那么称事件A与事件B互为对立.事件A的对立事件记为
易错提醒
01
02
03
01
若两个事件对立,则这两个事件是互斥事件;反之,若两个事件是互斥事件,则这两个事件未必是对立事件,对立事件是特殊的互斥事件
古典概率
02
02
03
03
概率的定义
对随机事件发生可能性大小的度重(数值)称为事件的概率,事件 A的概率用P(A)表示.
古典概型
古典概型的定义
①有限性:样本空间的样本点只有有限个;
②等可能性:每个样本点发生的可能性相等.
我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型.
古典概率
02
02
03
03
古典概型的判断标准
一个试验是否为古典概型,在于这个试验是否具有古典概型的两个特点:有限性和等可能性.并不是所有的试验都是古典概型.
下列三类试验都不是古典概型:
①样本点(基本事件)个数有限,但非等可能;
②样本点(基本事件)个数无限,但等可能;
③样本点(基本事件)个数无限,也不等可能.
古典概率
02
02
03
03
古典概型的概率公式
一般地,设试验E是古典概型,样本空间 包含n个样本点,事件 A包含其中的k个样本点,则定义事件A的概率
其中,n(A)和n( )分别表示事件A和样本空间包含的样本点个数.
古典概率
02
02
03
03
概率的基本性质
{5940675A-B579-460E-94D1-54222C63F5DA}性质1
对任意的事件A,都有P(A)≥0
性质2
必然事件的概率为1,不可能事件的概率为0,即P( )=1,P( )=0
性质3
互斥事件的概率加法公式:如果事件A与事件B互斥,那么P(AUB)=P(A)+P(B)
性质4
对立事件的概率公式:如果事件A与事件B互为对立事件,那么P(B)=1-P(A),P(A)=1-P(B)
性质5
概率的单调性:如果A B,那么P(A)≤P(B)
性质6
概率的计算公式:设A ,B是一个随机试验中的两个事件,我们有P(AUB)=P(A)+P(B)-P(A∩B).特别地,当A与B互斥,即A∩B= 时.可得到性质3
例1
经典例题
有编号为1,2,3的三个小球和编号为1,2,3的三个盒子,将三个小球逐个随机的放入三个盒子中,每个盒子放一个球,每只小球的放置是相互独立的
(1)共有多少种不同的放法?请列举出来;
(2)求盒中放置的球的编号与所在盒的编号均不相同的概率.
解析
经典例题
【详解】
解:(1)共有六种不同的放法,按盒子号1,2,3的顺序放入小球的情况为(1,2,3);(1,3,2);(2,3,1);(2,1,3);(3,2,1);(3,1,2);
(2)设所求事件为A,则A包含有(2,3,1);(3,1,2)两个基本事件并且每个基本事件等可能故
例2
经典例题
皮埃尔·德·费马,法国律师和业余数学家,被誉为“业余数学家之王”,对数学作出了重大贡献,其中在1636年发现了:若p是质数,且a,p互质,那么a的 次方除以p的余数恒等于1,后来人们称该定理为费马小定理.依此定理若在数集 中任取两个数,其中一个作为p,另一个作为a,则所取两个数符合费马小定理的概率为( )
A. B. C. D.
解析
经典例题
【详解】
从 中任取2个数:
共12种方法;
符合题意的 共有: 共有7种,
所以所取两个数符合费马小定理的概率为
故选:A.
随堂练习
1.将甲?乙等4名交警随机分配到两个不同路口疏导交通,每个路口两人,则甲和乙不在同一路口的概率为( C )
A. B. C. D.
随堂练习
2.从1,2,3,4数字中任取三个不同的数字,则所抽取的三个数字之和能被整除的概率为( C )
A. B. C. D.
感谢聆听
10.1随机事件与概率
知道样本空间、随机事件、必然事件、不可能事件的概念
01
知道事件的包含关系,并事件,交事件,互斥事件,对立事件等概念
02
知道古典概率的基本特征与计算公式,并解决实际问题
03
学习目标
有限样本空间与随机事件
01
02
03
01
随机试验
我们把对随机现象的实现和对它的观察称为随机试验,简称试验,常用字母E表示.例如,抛一枚硬币、掷一个均匀的骰子等,都可以看成随机试验.
有限样本空间与随机事件
02
02
03
01
样本点和样本空间
(1)定义:我们把随机试验E的每个可能的基本结果称为样本点,全体样本点的集合称为试验E的样本空间
(2)表示:一般地,我们用 表示样本空间,用 表示样本点
(3)有限样本空间:如果一个随机试验有n个可能结果 ,则称样本空间 = 为有限样本空间
有限样本空间与随机事件
02
02
03
01
事件
(1)随机事件:我们将样本空间 的子集称为随机事件,简称事件,并把只包含一个样本点的事件称为基本事件.随机事件一般用大写字母A,B,C,表示,在每次试验中,当且仅当A中某个样本点出现时,称为事件A发生.
(2)必然事件: 作为自身的子集,包含了所有的样本点,在每次试验中总有一个样本点发生,所以 总会发生,我们称 为必然事件.
(3)不可能事件:空集 中不包含任何样本点,在每次试验中都不会发生,我们称 为不可能事件.
有限样本空间与随机事件
02
02
03
01
“守株待兔”是随机事件
“太阳的东升西落”是必然事件
“水中捞月”是不可能事件
事件的关系和运算
02
02
03
02
{5940675A-B579-460E-94D1-54222C63F5DA}
含义
包含关系
一般地,若事件A发生,则事件B一定发生,找们就称事件B包含事件A(或事件A包含于事件B),记作B A(或A B)
相等关系
如果事件B包含事件A,事件A也包含事件B,即B A且A B,则称事件A与事件B相等,记作A=B
并事件(和事件)
一般地,事件A与事件B至少有一个发生,这样的一个事件中的样本点或者在事件A中,或者在事件B中,我们称这个事件为事件A与事件B的并事件(或和事件),记作AUB(或A+B)
事件的关系和运算
02
02
03
02
{5940675A-B579-460E-94D1-54222C63F5DA}交事件(积事件)
一般地,事件A与事件B同时发生,这样的一个事件中的样本点既在事件A中,也在事件B中,我们称这样的一个事件为事件A与事件B的交事件(或积事件),记作A∩B(或AB)
互斥事件
一股地,如果事件A与事件B不能同时发生,也就是说A∩B是一个不可能事件,A∩B= ,则称事件A与事件B互斥(或互不相容)
对立事件
一般地,如果事件A和事件B在任何次试验中有且仅有一个发生,即AUB= ,且A∩B= ,那么称事件A与事件B互为对立.事件A的对立事件记为
易错提醒
01
02
03
01
若两个事件对立,则这两个事件是互斥事件;反之,若两个事件是互斥事件,则这两个事件未必是对立事件,对立事件是特殊的互斥事件
古典概率
02
02
03
03
概率的定义
对随机事件发生可能性大小的度重(数值)称为事件的概率,事件 A的概率用P(A)表示.
古典概型
古典概型的定义
①有限性:样本空间的样本点只有有限个;
②等可能性:每个样本点发生的可能性相等.
我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型.
古典概率
02
02
03
03
古典概型的判断标准
一个试验是否为古典概型,在于这个试验是否具有古典概型的两个特点:有限性和等可能性.并不是所有的试验都是古典概型.
下列三类试验都不是古典概型:
①样本点(基本事件)个数有限,但非等可能;
②样本点(基本事件)个数无限,但等可能;
③样本点(基本事件)个数无限,也不等可能.
古典概率
02
02
03
03
古典概型的概率公式
一般地,设试验E是古典概型,样本空间 包含n个样本点,事件 A包含其中的k个样本点,则定义事件A的概率
其中,n(A)和n( )分别表示事件A和样本空间包含的样本点个数.
古典概率
02
02
03
03
概率的基本性质
{5940675A-B579-460E-94D1-54222C63F5DA}性质1
对任意的事件A,都有P(A)≥0
性质2
必然事件的概率为1,不可能事件的概率为0,即P( )=1,P( )=0
性质3
互斥事件的概率加法公式:如果事件A与事件B互斥,那么P(AUB)=P(A)+P(B)
性质4
对立事件的概率公式:如果事件A与事件B互为对立事件,那么P(B)=1-P(A),P(A)=1-P(B)
性质5
概率的单调性:如果A B,那么P(A)≤P(B)
性质6
概率的计算公式:设A ,B是一个随机试验中的两个事件,我们有P(AUB)=P(A)+P(B)-P(A∩B).特别地,当A与B互斥,即A∩B= 时.可得到性质3
例1
经典例题
有编号为1,2,3的三个小球和编号为1,2,3的三个盒子,将三个小球逐个随机的放入三个盒子中,每个盒子放一个球,每只小球的放置是相互独立的
(1)共有多少种不同的放法?请列举出来;
(2)求盒中放置的球的编号与所在盒的编号均不相同的概率.
解析
经典例题
【详解】
解:(1)共有六种不同的放法,按盒子号1,2,3的顺序放入小球的情况为(1,2,3);(1,3,2);(2,3,1);(2,1,3);(3,2,1);(3,1,2);
(2)设所求事件为A,则A包含有(2,3,1);(3,1,2)两个基本事件并且每个基本事件等可能故
例2
经典例题
皮埃尔·德·费马,法国律师和业余数学家,被誉为“业余数学家之王”,对数学作出了重大贡献,其中在1636年发现了:若p是质数,且a,p互质,那么a的 次方除以p的余数恒等于1,后来人们称该定理为费马小定理.依此定理若在数集 中任取两个数,其中一个作为p,另一个作为a,则所取两个数符合费马小定理的概率为( )
A. B. C. D.
解析
经典例题
【详解】
从 中任取2个数:
共12种方法;
符合题意的 共有: 共有7种,
所以所取两个数符合费马小定理的概率为
故选:A.
随堂练习
1.将甲?乙等4名交警随机分配到两个不同路口疏导交通,每个路口两人,则甲和乙不在同一路口的概率为( C )
A. B. C. D.
随堂练习
2.从1,2,3,4数字中任取三个不同的数字,则所抽取的三个数字之和能被整除的概率为( C )
A. B. C. D.
感谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
