10.2事件的相互独立性-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(机构适用)(16张PPT)
文档属性
| 名称 | 10.2事件的相互独立性-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(机构适用)(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 323.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 17:09:11 | ||
图片预览






文档简介
第十章概率
10.2事件的相互独立性
弄清相互独立事件的概念与意义
01
能够利用相互独立事件的概率公式求解简单的概率问题
02
能够解决实际问题中的概率问题
03
学习目标
思考与探究
02
02
03
思考1:在大小均匀的5个球中有3个红球,2个白球,每次取一个,不放回的取2次,求在已知第一次取到红球的条件下,第二次取到红球的概率?
思考2:在大小均匀的5个球中有3个红球,2个白球,每次取一个,有放回的取2次,求在已知第一次取到红球的条件下,第二次取到红球的概率?
事件的相互独立性
01
02
03
01
(1)定义:对任意两个事件A与B.如果P(AB)=P(A)P(B)成立,则称事件A与事件B相互独立,简称为独立.
(2)性质:如果事件A与事件B相互独立,那么A与,不与B,与B也相互独立
(3)"A与B相互独立"是“P(AB)=P(A)P(B)"的充要条件
(4)两个事件相互独立的概念也可以推广到有限个事件,即“相互独立”的充要条件是“其中任意有限个事件同时发生的概率都等于它们的概率之积”
易错提醒
01
02
03
01
多个事件独立与互斥的区别
如果三个事件A,B,C两两互斥,那么概率加法公式
成立,但当三个事件A,B,C两两独立时,等式
不一定成立
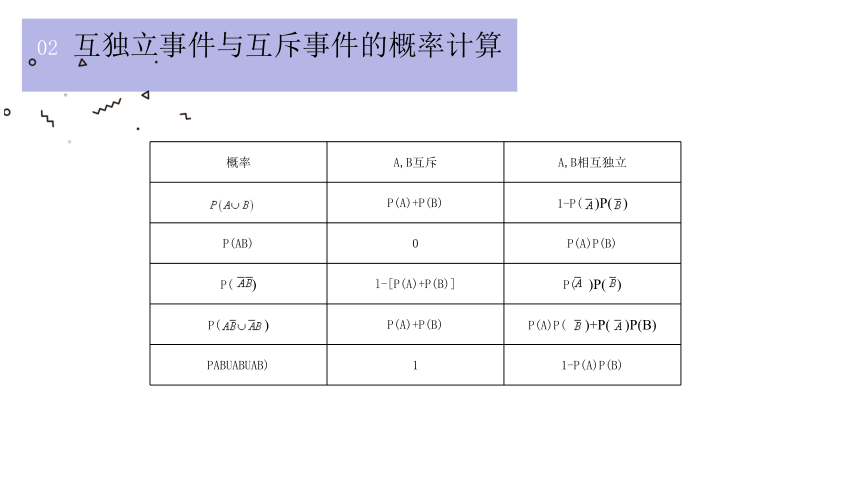
互独立事件与互斥事件的概率计算
02
02
03
02
已知两个事件A,B,它们的概率为P(A),P(B),将A,B中至少有一个发生记为事件A B,都发生记为事件AB,都不发生记为事件 ,恰有一个发生记为事件 ,至多有一个发生记为事件
互独立事件与互斥事件的概率计算
02
02
03
02
{5940675A-B579-460E-94D1-54222C63F5DA}概率
A,B互斥
A,B相互独立
P(A)+P(B)
1-P( )P( )
P(AB)
0
P(A)P(B)
P( )
l-[P(A)+P(B)]
P( )P( )
P( )
P(A)+P(B)
P(A)P( )+P( )P(B)
PABUABUAB)
1
1-P(A)P(B)
名师点拨
01
02
03
01
互斥事件、相互独立事件的综合应用
(1)简单计算问题
将题中所求事件转化为若干个独立事件的交事件,利用独立事件的性质和推广求解
(2)复杂计算问题
先将问题划分为若干个彼此互斥的事件,再运用互斥事件的概率加法公式和相互独立事件的概率计算公式求解
例1
经典例题
某商场对购买一定量的商品的顾客进行抽奖活动,活动规则是:一个袋中有大小、形状相同的红、黑球各一个,顾客从中依次有放回地随机摸取3次,每次摸取一个球,摸到红球时得2分,摸到黑球时得1分,顾客3次摸球所得总分超过4分获得奖品.
问题:
(1)如何确定此试验的样本空间?
(2)设“顾客获奖”为事件A,则A中含有哪些样本点?
(3)如何求出事件 “顾客获奖”的概率?
解析
经典例题
【详解】
(1)样本空间 (红,红,红),(红,红,黑),(红,黑,红),(红,黑,黑),(黑,红,红),(黑,红,黑)(黑,黑,红),(黑,黑,黑)}.
(2)提示:“顾客获奖”就是顾客得分为5分或6分,即三次摸到3个红球或2个红球1个黑球,因此事件A中含有的样本点有(红,红,红),(红,红,黑),(红,黑,红),(黑,红,红).
(3)提示:依题意知该试验是古典概型,事件A包含的样本点数为4,由问题1知,样本点总数为8,所以事件A的概率 .
例2
经典例题
如图所示,1,2,3表示三个开关,若在某段时间内它们每个正常工作的概率都是0.9,那么此系统的可靠性是( )
A.0.999 B.0.981 C.0.980 D.0.729
解析
经典例题
【详解】
由题意,开关1、2在某段时间内均正常工作的概率 ,
开关3正常工作的概率 ,
故该系统正常工作的概率 ,
所以该系统的可靠性为0.981.
故选:B.
随堂练习
1.某兴趣小组从包括甲、乙的小组成员中任选3人参加活动,若甲、乙至多有一人被选中的概率是,则甲、乙均被选中的概率是( B )
A. B. C. D.
随堂练习
2.若A,B为互斥事件, , ,则 ( B )
A.0.1 B.0.3 C.0.4 D.0.7
随堂练习
3.接种疫苗是预防和控制传染病最经济、有效的公共卫生干预措施.根据实验数据,人在接种某种病毒疫苗后,有80%不会感染这种病毒,若有4人接种了这种疫苗,则最多1人被感染的概率为( A )
A. B. C. D.
感谢聆听
10.2事件的相互独立性
弄清相互独立事件的概念与意义
01
能够利用相互独立事件的概率公式求解简单的概率问题
02
能够解决实际问题中的概率问题
03
学习目标
思考与探究
02
02
03
思考1:在大小均匀的5个球中有3个红球,2个白球,每次取一个,不放回的取2次,求在已知第一次取到红球的条件下,第二次取到红球的概率?
思考2:在大小均匀的5个球中有3个红球,2个白球,每次取一个,有放回的取2次,求在已知第一次取到红球的条件下,第二次取到红球的概率?
事件的相互独立性
01
02
03
01
(1)定义:对任意两个事件A与B.如果P(AB)=P(A)P(B)成立,则称事件A与事件B相互独立,简称为独立.
(2)性质:如果事件A与事件B相互独立,那么A与,不与B,与B也相互独立
(3)"A与B相互独立"是“P(AB)=P(A)P(B)"的充要条件
(4)两个事件相互独立的概念也可以推广到有限个事件,即“相互独立”的充要条件是“其中任意有限个事件同时发生的概率都等于它们的概率之积”
易错提醒
01
02
03
01
多个事件独立与互斥的区别
如果三个事件A,B,C两两互斥,那么概率加法公式
成立,但当三个事件A,B,C两两独立时,等式
不一定成立
互独立事件与互斥事件的概率计算
02
02
03
02
已知两个事件A,B,它们的概率为P(A),P(B),将A,B中至少有一个发生记为事件A B,都发生记为事件AB,都不发生记为事件 ,恰有一个发生记为事件 ,至多有一个发生记为事件
互独立事件与互斥事件的概率计算
02
02
03
02
{5940675A-B579-460E-94D1-54222C63F5DA}概率
A,B互斥
A,B相互独立
P(A)+P(B)
1-P( )P( )
P(AB)
0
P(A)P(B)
P( )
l-[P(A)+P(B)]
P( )P( )
P( )
P(A)+P(B)
P(A)P( )+P( )P(B)
PABUABUAB)
1
1-P(A)P(B)
名师点拨
01
02
03
01
互斥事件、相互独立事件的综合应用
(1)简单计算问题
将题中所求事件转化为若干个独立事件的交事件,利用独立事件的性质和推广求解
(2)复杂计算问题
先将问题划分为若干个彼此互斥的事件,再运用互斥事件的概率加法公式和相互独立事件的概率计算公式求解
例1
经典例题
某商场对购买一定量的商品的顾客进行抽奖活动,活动规则是:一个袋中有大小、形状相同的红、黑球各一个,顾客从中依次有放回地随机摸取3次,每次摸取一个球,摸到红球时得2分,摸到黑球时得1分,顾客3次摸球所得总分超过4分获得奖品.
问题:
(1)如何确定此试验的样本空间?
(2)设“顾客获奖”为事件A,则A中含有哪些样本点?
(3)如何求出事件 “顾客获奖”的概率?
解析
经典例题
【详解】
(1)样本空间 (红,红,红),(红,红,黑),(红,黑,红),(红,黑,黑),(黑,红,红),(黑,红,黑)(黑,黑,红),(黑,黑,黑)}.
(2)提示:“顾客获奖”就是顾客得分为5分或6分,即三次摸到3个红球或2个红球1个黑球,因此事件A中含有的样本点有(红,红,红),(红,红,黑),(红,黑,红),(黑,红,红).
(3)提示:依题意知该试验是古典概型,事件A包含的样本点数为4,由问题1知,样本点总数为8,所以事件A的概率 .
例2
经典例题
如图所示,1,2,3表示三个开关,若在某段时间内它们每个正常工作的概率都是0.9,那么此系统的可靠性是( )
A.0.999 B.0.981 C.0.980 D.0.729
解析
经典例题
【详解】
由题意,开关1、2在某段时间内均正常工作的概率 ,
开关3正常工作的概率 ,
故该系统正常工作的概率 ,
所以该系统的可靠性为0.981.
故选:B.
随堂练习
1.某兴趣小组从包括甲、乙的小组成员中任选3人参加活动,若甲、乙至多有一人被选中的概率是,则甲、乙均被选中的概率是( B )
A. B. C. D.
随堂练习
2.若A,B为互斥事件, , ,则 ( B )
A.0.1 B.0.3 C.0.4 D.0.7
随堂练习
3.接种疫苗是预防和控制传染病最经济、有效的公共卫生干预措施.根据实验数据,人在接种某种病毒疫苗后,有80%不会感染这种病毒,若有4人接种了这种疫苗,则最多1人被感染的概率为( A )
A. B. C. D.
感谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
