2020-2021学年高中数学人教A版必修五第二章2.3 等差数列的前n项和课件(共19张PPT)
文档属性
| 名称 | 2020-2021学年高中数学人教A版必修五第二章2.3 等差数列的前n项和课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 488.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 17:14:25 | ||
图片预览






文档简介
1
2.3.1等差数列的前n项和
七兄弟分财产,老七得2,后一个比前一个多得1/6,问所分财产共有多少?
数学泥版MS 1844
(约公元前2050年)
数列求和问题
3
问题一:
一个堆放铅笔的V形架的最下面一层放1支铅笔,往上每一层都比它下面一层多放一支,最上面一层放100支。 这个V形架上共放着多少支铅笔?
高斯:(1777-1855)德国著名数学家,他的研究涉及数学的各个领域,是历史上最伟大的数学家之一,被誉为“数学王子”。
5
问题二:
倒序相加法
1
2
3
n
n
n-1
n-2
1
6
问题三:
等差数列前项和公式:
探究:能把以上问题的解法推广到求一般等差数列的前 项和吗?
7
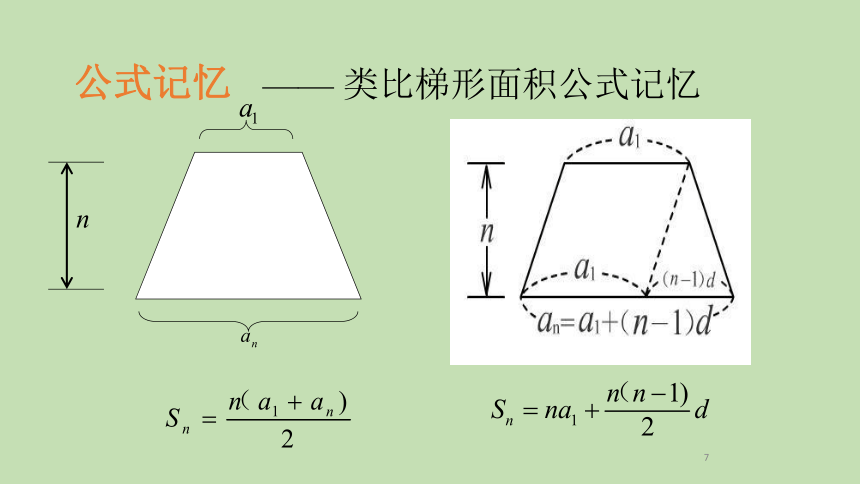
公式记忆
—— 类比梯形面积公式记忆
8
问题五:
等差数列前项和公式:
两个求和公式有何异同点?能够解决什么问题?
类型1:求和公式的基本运用
类型1:公式的基本运用
变式提升:
13
公式变形与探究
类型2:等差数列前n项和的最值问题
15
小结:
(1)等差数列求和方法:倒序相加法
(2)等差数列前n项和与二次函数的关系
(3)数形结合的数学思想方法
作业布置:
课时练 第30页 要点一和要点二;
第31页的随堂检测
谢谢!
欢迎指正!
2.3.1等差数列的前n项和
七兄弟分财产,老七得2,后一个比前一个多得1/6,问所分财产共有多少?
数学泥版MS 1844
(约公元前2050年)
数列求和问题
3
问题一:
一个堆放铅笔的V形架的最下面一层放1支铅笔,往上每一层都比它下面一层多放一支,最上面一层放100支。 这个V形架上共放着多少支铅笔?
高斯:(1777-1855)德国著名数学家,他的研究涉及数学的各个领域,是历史上最伟大的数学家之一,被誉为“数学王子”。
5
问题二:
倒序相加法
1
2
3
n
n
n-1
n-2
1
6
问题三:
等差数列前项和公式:
探究:能把以上问题的解法推广到求一般等差数列的前 项和吗?
7
公式记忆
—— 类比梯形面积公式记忆
8
问题五:
等差数列前项和公式:
两个求和公式有何异同点?能够解决什么问题?
类型1:求和公式的基本运用
类型1:公式的基本运用
变式提升:
13
公式变形与探究
类型2:等差数列前n项和的最值问题
15
小结:
(1)等差数列求和方法:倒序相加法
(2)等差数列前n项和与二次函数的关系
(3)数形结合的数学思想方法
作业布置:
课时练 第30页 要点一和要点二;
第31页的随堂检测
谢谢!
欢迎指正!
