2020-2021学年湘教版八年级数学下册期中综合练习(二)(word版含答案)
文档属性
| 名称 | 2020-2021学年湘教版八年级数学下册期中综合练习(二)(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 388.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-27 15:09:03 | ||
图片预览



文档简介
2020-2021学年湘教版八年级数学下册期中综合练习(二)附答案
一、选择题
如图,在
中,,,,
是
的平分线.若
,
分别是
和
上的动点,则
的最小值是
A.
B.
C.
D.
以下列各组数为边长,能构成直角三角形的是
A.
,,
B.
,,
C.
,,
D.
,,
在正方形网格中,
的位置如图所示,则
的值为
A.
B.
C.
D.
如图,已知
中,,,,
是
的垂直平分线,
交
于点
,连接
,则
A.
B.
C.
D.
河堤横断面如图所示,斜坡
的坡度
,,则
的长是
A.
B.
C.
D.
如图,在
中,,,以
为圆心,小于
的任意长为半径画弧分别交
,
于点
和
,再分别以
,
为圆心,大于
的长为半径画弧,两弧交于点
,连接
并延长交
于点
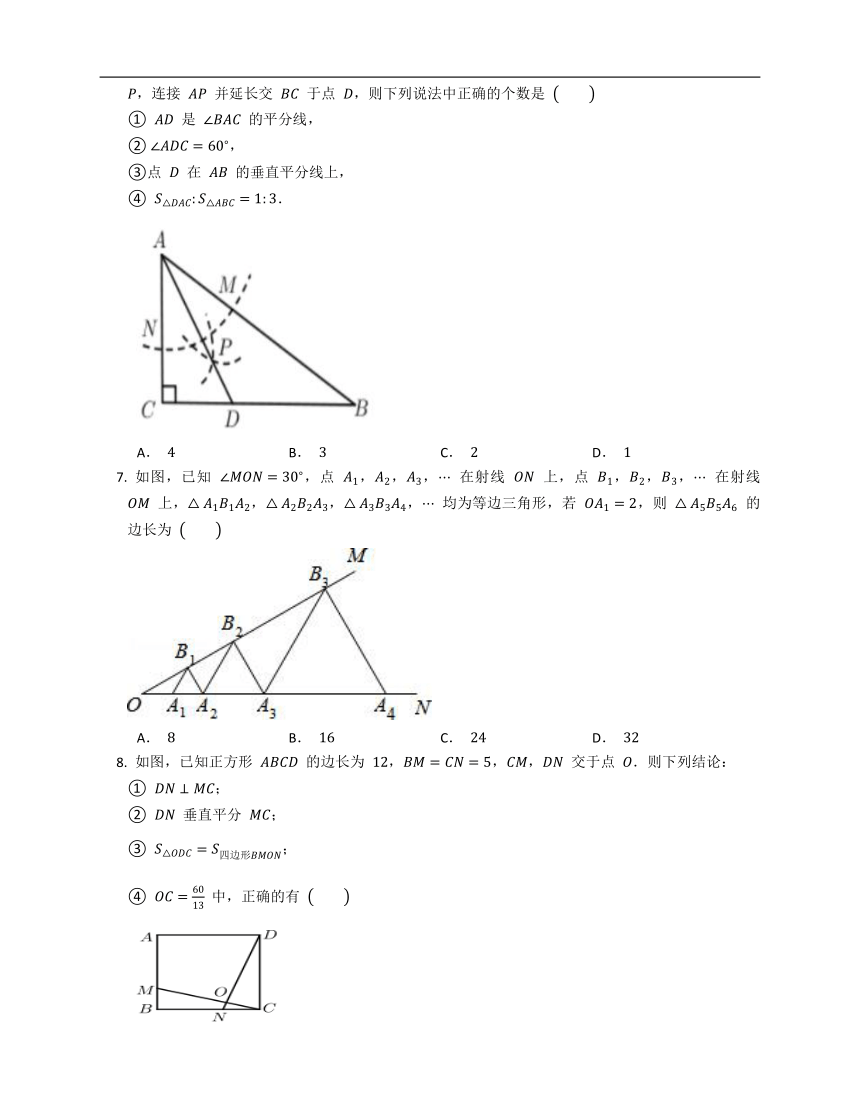
,则下列说法中正确的个数是
①
是
的平分线,
②
,
③点
在
的垂直平分线上,
④
.
A.
B.
C.
D.
如图,已知
,点
,,,
在射线
上,点
,,,
在射线
上,,,,
均为等边三角形,若
,则
的边长为
A.
B.
C.
D.
如图,已知正方形
的边长为
,,,
交于点
.则下列结论:
①
;
②
垂直平分
;
③
;
④
中,正确的有
A.
个
B.
个
C.
个
D.
个
已知:如图,在等边
中取点
,使得
,,
的长分别为
,,,将线段
以点
为旋转中心顺时针旋转
得到线段
,连接
,下列结论:
①
可以由
绕点
顺时针旋转
得到;
②点
与点
的距离为
;
③
;
④
.
其中正确的结论有
A.①②④
B.①③④
C.①②③
D.②③④
如图所示,在
中,,
于点
,
是
的中点,若
,则以下结论错误的是
A.
B.
C.
D.
边长为
的菱形,一条对角线长是
,则另一条对角线的长是
.
A.
B.
C.
D.
如图,
是
斜边
上的高,将
沿
折叠,
点恰好落在
的中点
处,则
等于
A.
B.
C.
D.
已知
,,
为内心,
交
于
,,,则
A.
B.
C.
D.
二、填空题
如图,
是等边三角形,
是
延长线上一点,
于点
,
于点
.若
,,则
的长为
.
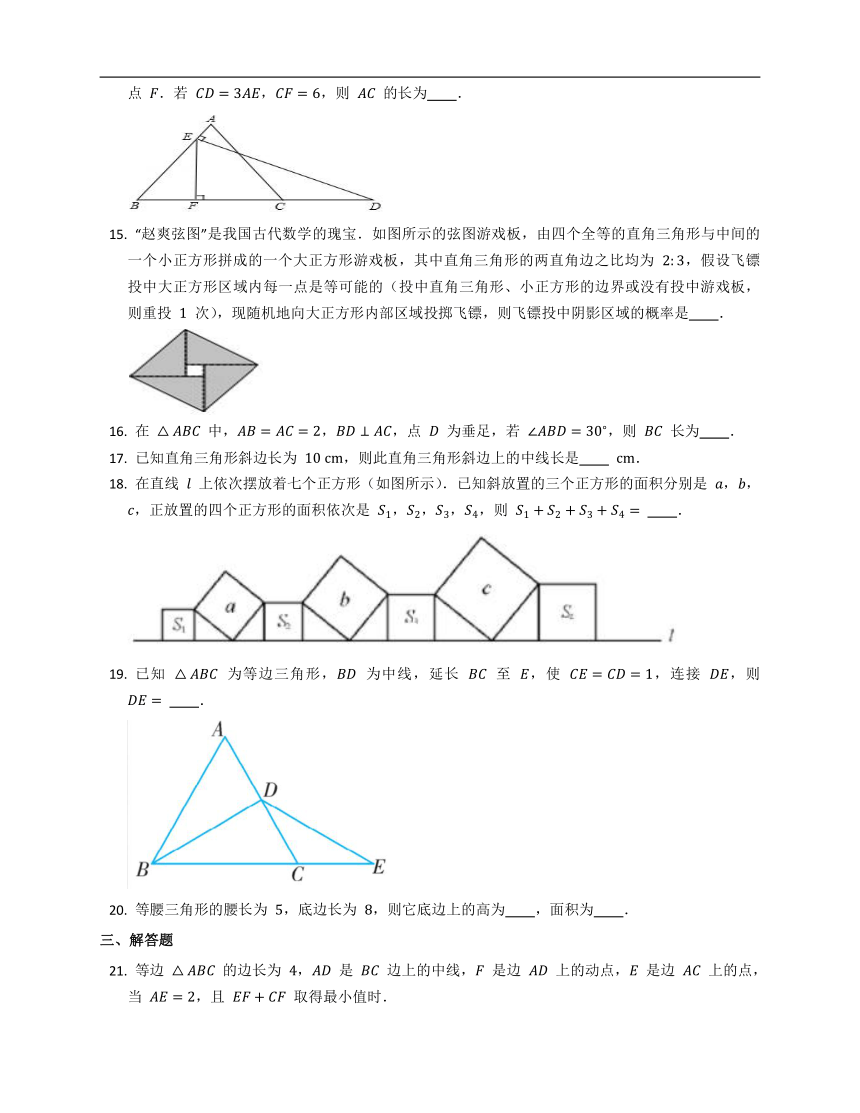
“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图游戏板,由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形游戏板,其中直角三角形的两直角边之比均为
,假设飞镖投中大正方形区域内每一点是等可能的(投中直角三角形、小正方形的边界或没有投中游戏板,则重投
次),现随机地向大正方形内部区域投掷飞镖,则飞镖投中阴影区域的概率是
.
在
中,,,点
为垂足,若
,则
长为
.
已知直角三角形斜边长为
,则此直角三角形斜边上的中线长是
.
在直线
上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是
,,,正放置的四个正方形的面积依次是
,,,,则
.
已知
为等边三角形,
为中线,延长
至
,使
,连接
,则
.
等腰三角形的腰长为
,底边长为
,则它底边上的高为
,面积为
.
三、解答题
等边
的边长为
,
是
边上的中线,
是边
上的动点,
是边
上的点,当
,且
取得最小值时.
(1)
能否求出
的度数?
(用“能”或“否”填空);
(2)
如果能,请你在图中作出点
(保留作图痕迹,不写证明).并直接写出
的度数;如果不能,请说明理由.
已知:如图,四边形
中,,,,,.求该四边形的面积.
如图,
为正方形
的边
上一动点(
与
,
不重合),连接
,过点
作
交
于点
,将
沿
所在的直线对折得到
,延长
交
的延长线于点
.
(1)
试探究
与
的数量关系,并证明你的结论;
(2)
当
,,求
的长;
(3)
当
时,
时,求
的长.
已知:如图,,,.求证:.
答案
一、选择题
1.
【答案】C
【解析】如图,过点
作
于点
,交
于点
,过点
作
于点
,
是
的平分线,
,这时
有最小值,即
的长度,
,,,
,
,
,
即
的最小值为
.
2.
【答案】A
3.
【答案】B
【解析】设小正方形的边长为
,则
,
.
4.
【答案】D
【解析】,,,
由勾股定理的逆定理可得
为直角三角形.
为
边的中垂线,
.
.
.
.
.
.
5.
【答案】B
【解析】
中,
斜坡
的坡度
,
,
,
,
故选:B.
6.
【答案】A
【解析】①连接
,,
在
与
中,
,
则
,
故
是
的平分线,故此选项正确;
②在
中,,,
,
是
的平分线,
,
,,故此选项正确;
③
,
,
点
在
的中垂线上,故此选项正确;
④
在
中,,
,
,
,
,
,故此选项正确.
故答案为:A.
7.
【答案】B
【解析】如图所示:
是等边三角形,
,,
,
,
,
又
,
,
,
,
,
,
是等边三角形,
,,
,
,,
,,
,,
,,;
故选:B.
8.
【答案】C
【解析】
四边形
是正方形,
,,
在
和
中,
,
,
又
,
,
,
,故①正确.
在
中,
,,
,
又
,,
,
,
,故②错误;
④正确.
,
,
,
即
,故③正确.
综上,正确的结论是①③④.
9.
【答案】C
【解析】连
,如图.
线段
以点
为旋转中心顺时针旋转
得到线段
,
,,
又
为等边三角形,
,,
,
,
可以由
绕点
顺时针旋转
得到,
①正确;
,,
为等边三角形,
,
②正确;
在
中,,,由①得到
,
,即
,
为直角三角形,且
,
由②得
,
,
③正确;
,
,
④不正确.
10.
【答案】D
11.
【答案】D
【解析】
菱形对角线互相垂直平分,且一条对角线长为
,
这条对角线的一半长
,
又
菱形的边长为
,
由勾股定理得,另一条对角线的一半长
,
另一条对角线长
.
12.
【答案】B
【解析】提示:
由已知得
,
.
,
.
13.
【答案】B
二、填空题
14.
【答案】
【解析】
与
相交于
,如图.
为等边三角形,
,,
,
,
,
,
,
,
设
,则
,,
在
中,,
,
,,
在
中,,
即
,解得
,
.
15.
【答案】
【解析】设两直角边分别是
,,则斜边即大正方形的边长为
,小正方形边长为
,
,,,
则针尖落在阴影区域的概率为
.
16.
【答案】
或
【解析】分为两种情况:
①如图1,
因为
,
所以
,
因为
,,
所以
,
所以
,
由勾股定理得:,
由勾股定理得:;
②如图2,
因为
,
所以
,
因为
,,
所以
,
所以
,
由勾股定理得:,
由勾股定理得:.
17.
【答案】
【解析】
直角三角形斜边长为
,
斜边上的中线长为
.
故答案为
.
18.
【答案】
【解析】
,,
,
,,
,
,
在直角
中,,
即
,
,,
,
同理
,
故可得
.
19.
【答案】
20.
【答案】
;
三、解答题
21.
【答案】
(1)
能
(2)
.
【解析】
(1)
利用轴对称的性质可以解决问题.
(2)
过
作
,交
于
.
,,
,
,
,
是
边上的中线,
是等边三角形,
,
,
,
,
和
关于
对称,
连接
交
于
,连接
,
则此时,
的值最小,
是等边三角形,
,,
,
.
22.
【答案】提示:连接
,可得
是直角三角形.则四边形面积为
平方厘米.
23.
【答案】
(1)
.
理由:
四边形
是正方形,
,,
.
,
,
.
在
和
中,
,
;
(2)
过点
作
于
,如图.
四边形
是正方形,
.
,
,,
,
.
四边形
是正方形,
,
.由折叠可得
,
,
.
设
,则有
,.
在
中,根据勾股定理可得
,
解得
.
的长为
;
(3)
过点
作
于
,如图.
四边形
是正方形,,,
.
,
,
.
设
,则有
,.
在
中,根据勾股定理可得
,
解得
,
.
的长为
.
24.
【答案】连接
.
,.
,
在
和
中,
.
.
一、选择题
如图,在
中,,,,
是
的平分线.若
,
分别是
和
上的动点,则
的最小值是
A.
B.
C.
D.
以下列各组数为边长,能构成直角三角形的是
A.
,,
B.
,,
C.
,,
D.
,,
在正方形网格中,
的位置如图所示,则
的值为
A.
B.
C.
D.
如图,已知
中,,,,
是
的垂直平分线,
交
于点
,连接
,则
A.
B.
C.
D.
河堤横断面如图所示,斜坡
的坡度
,,则
的长是
A.
B.
C.
D.
如图,在
中,,,以
为圆心,小于
的任意长为半径画弧分别交
,
于点
和
,再分别以
,
为圆心,大于
的长为半径画弧,两弧交于点
,连接
并延长交
于点
,则下列说法中正确的个数是
①
是
的平分线,
②
,
③点
在
的垂直平分线上,
④
.
A.
B.
C.
D.
如图,已知
,点
,,,
在射线
上,点
,,,
在射线
上,,,,
均为等边三角形,若
,则
的边长为
A.
B.
C.
D.
如图,已知正方形
的边长为
,,,
交于点
.则下列结论:
①
;
②
垂直平分
;
③
;
④
中,正确的有
A.
个
B.
个
C.
个
D.
个
已知:如图,在等边
中取点
,使得
,,
的长分别为
,,,将线段
以点
为旋转中心顺时针旋转
得到线段
,连接
,下列结论:
①
可以由
绕点
顺时针旋转
得到;
②点
与点
的距离为
;
③
;
④
.
其中正确的结论有
A.①②④
B.①③④
C.①②③
D.②③④
如图所示,在
中,,
于点
,
是
的中点,若
,则以下结论错误的是
A.
B.
C.
D.
边长为
的菱形,一条对角线长是
,则另一条对角线的长是
.
A.
B.
C.
D.
如图,
是
斜边
上的高,将
沿
折叠,
点恰好落在
的中点
处,则
等于
A.
B.
C.
D.
已知
,,
为内心,
交
于
,,,则
A.
B.
C.
D.
二、填空题
如图,
是等边三角形,
是
延长线上一点,
于点
,
于点
.若
,,则
的长为
.
“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图游戏板,由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形游戏板,其中直角三角形的两直角边之比均为
,假设飞镖投中大正方形区域内每一点是等可能的(投中直角三角形、小正方形的边界或没有投中游戏板,则重投
次),现随机地向大正方形内部区域投掷飞镖,则飞镖投中阴影区域的概率是
.
在
中,,,点
为垂足,若
,则
长为
.
已知直角三角形斜边长为
,则此直角三角形斜边上的中线长是
.
在直线
上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是
,,,正放置的四个正方形的面积依次是
,,,,则
.
已知
为等边三角形,
为中线,延长
至
,使
,连接
,则
.
等腰三角形的腰长为
,底边长为
,则它底边上的高为
,面积为
.
三、解答题
等边
的边长为
,
是
边上的中线,
是边
上的动点,
是边
上的点,当
,且
取得最小值时.
(1)
能否求出
的度数?
(用“能”或“否”填空);
(2)
如果能,请你在图中作出点
(保留作图痕迹,不写证明).并直接写出
的度数;如果不能,请说明理由.
已知:如图,四边形
中,,,,,.求该四边形的面积.
如图,
为正方形
的边
上一动点(
与
,
不重合),连接
,过点
作
交
于点
,将
沿
所在的直线对折得到
,延长
交
的延长线于点
.
(1)
试探究
与
的数量关系,并证明你的结论;
(2)
当
,,求
的长;
(3)
当
时,
时,求
的长.
已知:如图,,,.求证:.
答案
一、选择题
1.
【答案】C
【解析】如图,过点
作
于点
,交
于点
,过点
作
于点
,
是
的平分线,
,这时
有最小值,即
的长度,
,,,
,
,
,
即
的最小值为
.
2.
【答案】A
3.
【答案】B
【解析】设小正方形的边长为
,则
,
.
4.
【答案】D
【解析】,,,
由勾股定理的逆定理可得
为直角三角形.
为
边的中垂线,
.
.
.
.
.
.
5.
【答案】B
【解析】
中,
斜坡
的坡度
,
,
,
,
故选:B.
6.
【答案】A
【解析】①连接
,,
在
与
中,
,
则
,
故
是
的平分线,故此选项正确;
②在
中,,,
,
是
的平分线,
,
,,故此选项正确;
③
,
,
点
在
的中垂线上,故此选项正确;
④
在
中,,
,
,
,
,
,故此选项正确.
故答案为:A.
7.
【答案】B
【解析】如图所示:
是等边三角形,
,,
,
,
,
又
,
,
,
,
,
,
是等边三角形,
,,
,
,,
,,
,,
,,;
故选:B.
8.
【答案】C
【解析】
四边形
是正方形,
,,
在
和
中,
,
,
又
,
,
,
,故①正确.
在
中,
,,
,
又
,,
,
,
,故②错误;
④正确.
,
,
,
即
,故③正确.
综上,正确的结论是①③④.
9.
【答案】C
【解析】连
,如图.
线段
以点
为旋转中心顺时针旋转
得到线段
,
,,
又
为等边三角形,
,,
,
,
可以由
绕点
顺时针旋转
得到,
①正确;
,,
为等边三角形,
,
②正确;
在
中,,,由①得到
,
,即
,
为直角三角形,且
,
由②得
,
,
③正确;
,
,
④不正确.
10.
【答案】D
11.
【答案】D
【解析】
菱形对角线互相垂直平分,且一条对角线长为
,
这条对角线的一半长
,
又
菱形的边长为
,
由勾股定理得,另一条对角线的一半长
,
另一条对角线长
.
12.
【答案】B
【解析】提示:
由已知得
,
.
,
.
13.
【答案】B
二、填空题
14.
【答案】
【解析】
与
相交于
,如图.
为等边三角形,
,,
,
,
,
,
,
,
设
,则
,,
在
中,,
,
,,
在
中,,
即
,解得
,
.
15.
【答案】
【解析】设两直角边分别是
,,则斜边即大正方形的边长为
,小正方形边长为
,
,,,
则针尖落在阴影区域的概率为
.
16.
【答案】
或
【解析】分为两种情况:
①如图1,
因为
,
所以
,
因为
,,
所以
,
所以
,
由勾股定理得:,
由勾股定理得:;
②如图2,
因为
,
所以
,
因为
,,
所以
,
所以
,
由勾股定理得:,
由勾股定理得:.
17.
【答案】
【解析】
直角三角形斜边长为
,
斜边上的中线长为
.
故答案为
.
18.
【答案】
【解析】
,,
,
,,
,
,
在直角
中,,
即
,
,,
,
同理
,
故可得
.
19.
【答案】
20.
【答案】
;
三、解答题
21.
【答案】
(1)
能
(2)
.
【解析】
(1)
利用轴对称的性质可以解决问题.
(2)
过
作
,交
于
.
,,
,
,
,
是
边上的中线,
是等边三角形,
,
,
,
,
和
关于
对称,
连接
交
于
,连接
,
则此时,
的值最小,
是等边三角形,
,,
,
.
22.
【答案】提示:连接
,可得
是直角三角形.则四边形面积为
平方厘米.
23.
【答案】
(1)
.
理由:
四边形
是正方形,
,,
.
,
,
.
在
和
中,
,
;
(2)
过点
作
于
,如图.
四边形
是正方形,
.
,
,,
,
.
四边形
是正方形,
,
.由折叠可得
,
,
.
设
,则有
,.
在
中,根据勾股定理可得
,
解得
.
的长为
;
(3)
过点
作
于
,如图.
四边形
是正方形,,,
.
,
,
.
设
,则有
,.
在
中,根据勾股定理可得
,
解得
,
.
的长为
.
24.
【答案】连接
.
,.
,
在
和
中,
.
.
同课章节目录
