2020-2021学年湘教新版八年级下册数学《第2章 四边形》单元测试卷(word有答案)
文档属性
| 名称 | 2020-2021学年湘教新版八年级下册数学《第2章 四边形》单元测试卷(word有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 222.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-27 23:15:12 | ||
图片预览


文档简介
2020-2021学年湘教新版八年级下册数学《第2章
四边形》单元测试卷
一.选择题
1.如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
A.3cm
B.6cm
C.9cm
D.12cm
2.四边形具有不稳定性,对于四条边长确定的四边形.当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′.若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )
A.1
B.
C.
D.
3.某人到瓷砖商店去买一种多边形形状的瓷砖用来铺设无缝地板,他购买的瓷砖形状不可以是( )
A.正三角形
B.长方形
C.正八边形
D.正六边形
4.下面性质中,平行四边形不一定具备的是( )
A.对角互补
B.邻角互补
C.对角相等
D.对角线互相平分
5.如果n边形的内角和是它外角和的4倍,则n等于( )
A.7
B.8
C.10
D.9
6.如果过一个多边形的一个顶点的对角线有6条,则该多边形是( )
A.九边形
B.八边形
C.七边形
D.六边形
7.对角线互相垂直且相等的四边形是( )
A.菱形
B.矩形
C.正方形
D.以上结论都不对
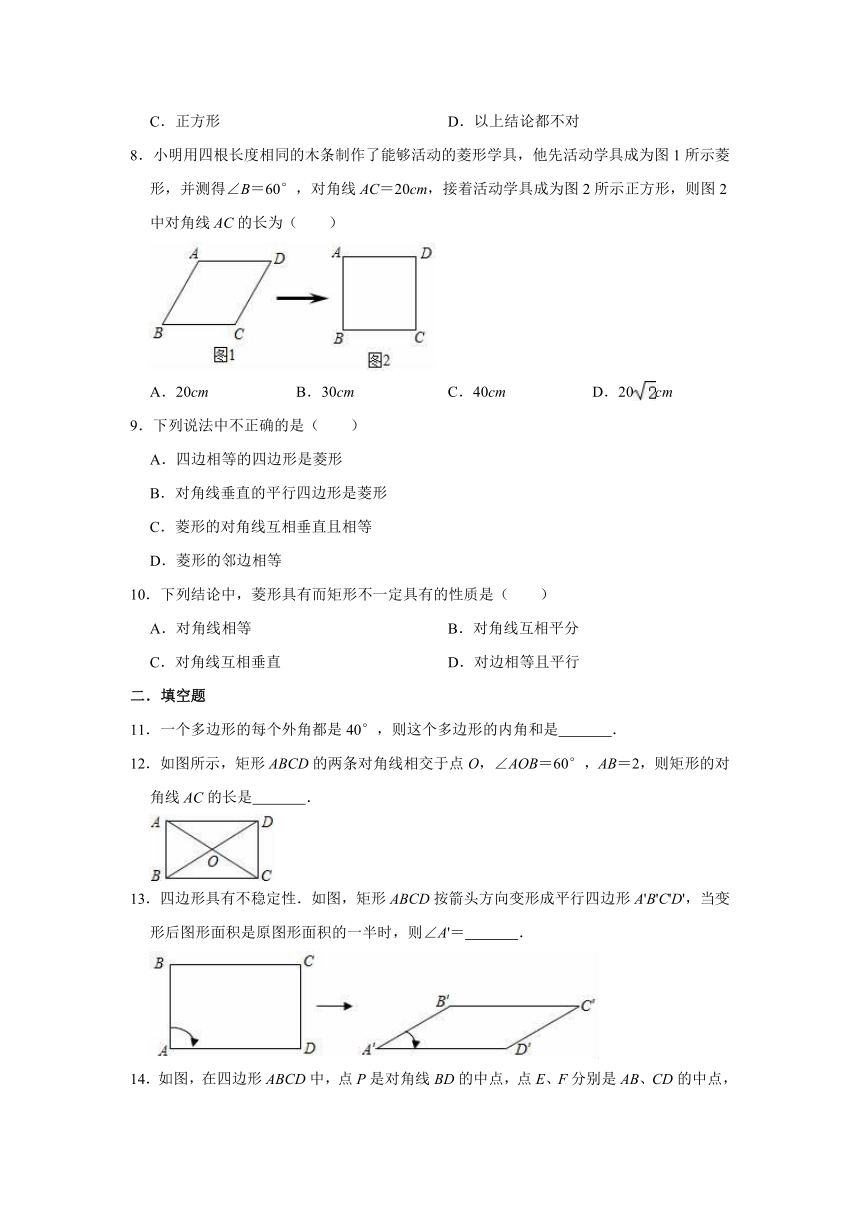
8.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
9.下列说法中不正确的是( )
A.四边相等的四边形是菱形
B.对角线垂直的平行四边形是菱形
C.菱形的对角线互相垂直且相等
D.菱形的邻边相等
10.下列结论中,菱形具有而矩形不一定具有的性质是( )
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对边相等且平行
二.填空题
11.一个多边形的每个外角都是40°,则这个多边形的内角和是
.
12.如图所示,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是
.
13.四边形具有不稳定性.如图,矩形ABCD按箭头方向变形成平行四边形A'B'C'D',当变形后图形面积是原图形面积的一半时,则∠A'=
.
14.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是
.
15.把边长为a的正三角形和正方形组合镶嵌,若用2个正方形,则还需
个正三角形才可以镶嵌.
16.菱形ABCD中,若周长是20cm,对角线AC=6cm,则对角线BD=
cm.
17.过多边形的某一个顶点的所有对角线可以把多边形分成5个三角形,则这个多边形是
边形.
18.如图,过平行四边形ABCD的对角找BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是
.
19.如图,下列条件之一能使?ABCD是菱形的有
(填序号)
①AC⊥BD;
②∠BAD=90°;
③AB=BC;
④AC=BD.
20.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则BD的长为
.
三.解答题
21.在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
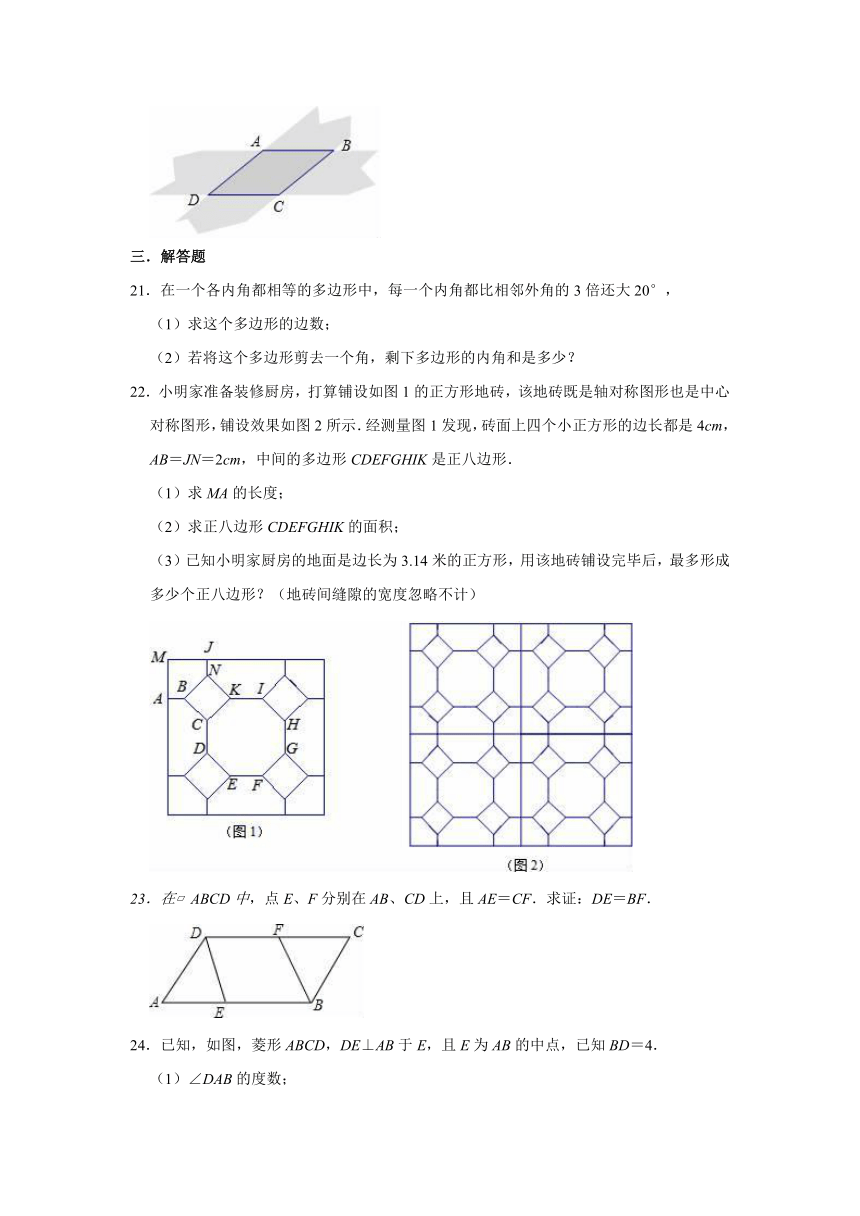
22.小明家准备装修厨房,打算铺设如图1的正方形地砖,该地砖既是轴对称图形也是中心对称图形,铺设效果如图2所示.经测量图1发现,砖面上四个小正方形的边长都是4cm,AB=JN=2cm,中间的多边形CDEFGHIK是正八边形.
(1)求MA的长度;
(2)求正八边形CDEFGHIK的面积;
(3)已知小明家厨房的地面是边长为3.14米的正方形,用该地砖铺设完毕后,最多形成多少个正八边形?(地砖间缝隙的宽度忽略不计)
23.在?ABCD中,点E、F分别在AB、CD上,且AE=CF.求证:DE=BF.
24.已知,如图,菱形ABCD,DE⊥AB于E,且E为AB的中点,已知BD=4.
(1)∠DAB的度数;
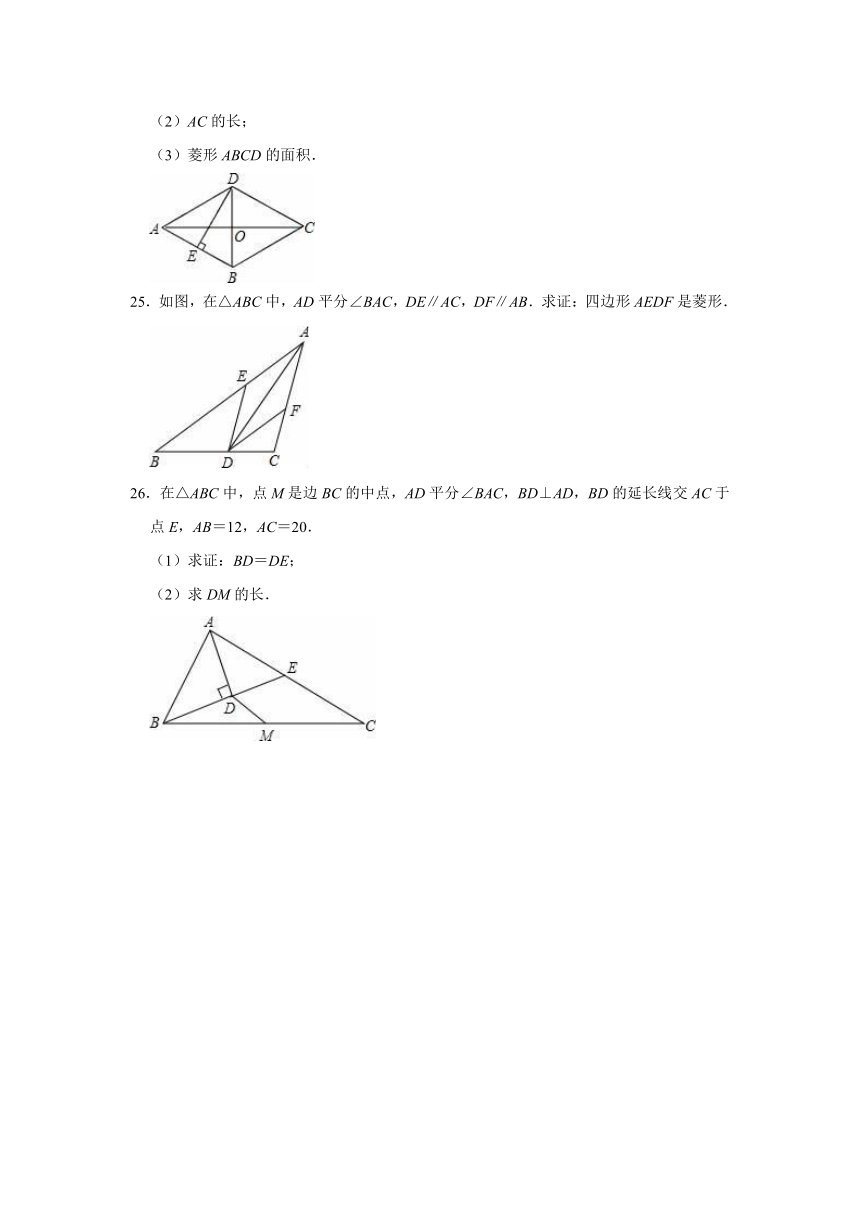
(2)AC的长;
(3)菱形ABCD的面积.
25.如图,在△ABC中,AD平分∠BAC,DE∥AC,DF∥AB.求证:四边形AEDF是菱形.
26.在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.
(1)求证:BD=DE;
(2)求DM的长.
参考答案与试题解析
一.选择题
1.解:∵四边形ABCD是平行四边形,
∴OA=OC;
又∵点E是BC的中点,
∴BE=CE,
∴AB=2OE=2×3=6(cm)
故选:B.
2.解:根据题意可知菱形ABC′D′的高等于AB的一半,
∴菱形ABC′D′的面积为,正方形ABCD的面积为AB2.
∴菱形ABC′D′的面积与正方形ABCD的面积之比是.
故选:B.
3.解;A、正三角形的内角是60°,6个正三角形可以密铺,故A可以;
B、长方形的内角是90°,4个长方形可以密铺,故B可以;
C、正八边形的内角是135°,2个正八边形有缝隙,3个正八边形重叠,故C不可以;
D、正六边形的内角是120°,3个正六边形可以密铺,故D可以;
故选:C.
4.解:∵平行四边形的对角相等,对角线互相平分,对边平行,即可得平行四边形的邻角互补;
∴B、C、D正确.
故选:A.
5.解:多边形的外角和是360°,根据题意得:
180°?(n﹣2)=360°×4,
解得n=10.
故选:C.
6.解:∵过一个多边形的一个顶点的对角线有6条,
∴多边形的边数为6+3=9,
∴这个多边形是九边形.
故选:A.
7.解:对角线互相垂直且相等,但不互相平分的四边形不是菱形、矩形、正方形,因为这三种四边形的对角线都互相平分.
故选:D.
8.解:如图1,图2中,连接AC.
图1中,∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC是等边三角形,
∴AB=BC=AC=20cm,
在图2中,∵四边形ABCD是正方形,
∴AB=BC,∠B=90°,
∴△ABC是等腰直角三角形,
∴AC=AB=20cm;
故选:D.
9.解:A.四边相等的四边形是菱形;正确;
B.对角线垂直的平行四边形是菱形;正确;
C.菱形的对角线互相垂直且相等;不正确;
D.菱形的邻边相等;正确;
故选:C.
10.解:A.因为矩形的对角线相等,所以A选项不符合题意;
B.因为矩形和菱形的对角线都互相平分,所以B选项不符合题意;
C.因为菱形对角线互相垂直,所以C选项符合题意;
D.因为矩形和菱形的对边都相等且平行,不符合题意.
故选:C.
二.填空题
11.解:设多边形的边数为n,
∵多边形的每个外角都等于40°,
∴n=360÷40=9,
∴这个多边形的内角和=(9﹣2)×180°=1260°.
故答案为1260°.
12.解:∵四边形ABCD是矩形,
∴AC=2AO,BD=2BO,AC=BD,
∴AO=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=2,
即AC=2AO=4,
故答案为:4.
13.解:∵,
∴平行四边形A'B'C'D'的底边A′D′边上的高等于A′B′的一半,
∴∠A'=30°.
故答案为:30°
14.解:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PF=BC,PE=AD,又AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=30°,
∴∠EPF=120°,
故答案为:120°.
15.解:∵正三角形的每个内角是60°,正方形的每个内角是90°,
又∵3×60°+2×90°=360°,
∴用2个正方形,则还需3个正三角形才可以镶嵌.
故答案为:3.
16.解:如图,∵菱形ABCD的周长是20cm,对角线AC=6cm,
∴AB=20÷4=5cm,AO=AC=3cm,
又∵AC⊥BD,
∴BO===4cm,
∴BD=2BO=8cm.
故答案为:8.
17.解:设多边形有n条边,
则n﹣2=5,
解得n=7.
故这个多边形是七边形.
故答案为:七.
18.解:∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2.
故答案为:S1=S2.
19.解:因为一组邻边相等的平行四边形是菱形;对角线互相垂直平分的四边形是菱形.则能使?ABCD是菱形的有①或③.
20.解:过点A作AE⊥BC于E,AF⊥CD于F,
∵两条纸条宽度相同,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵S?ABCD=BC?AE=CD?AF.
又∵AE=AF.
∴BC=CD,
∴四边形ABCD是菱形,
连接AC,BD相交于点O,
∴AC⊥BD,AO=AC=1,
∴BO==2,
∴BD=2BO=4,
故答案为:4.
三.解答题
21.解:(1)设多边形的一个外角为α,则与其相邻的内角等于3α+20°,
由题意,得(3α+20)+α=180°,解得α=40°.
即多边形的每个外角为40°.
又∵多边形的外角和为360°,
∴多边形的外角个数==9.
∴多边形的边数=9,
答:这个多边形的边数是9;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
当截线为经过对角2个顶点的直线时,多边形的边数减少了1条边,内角和=(9﹣2﹣1)×180°=1080°;
当截线为经过多边形一组对边的直线时,多边形的边数不变,内角和=(9﹣2)×180°=1260°;
当截线为只经过正方形一组邻边的一条直线时,多边形的边数增加一条边,内角和=(9﹣2+1)×180°=1440°.
答:将这个多边形剪去一个角,剩下多边形的内角和是1080°或1260°或1440°.
22.解:(1)连接BK和NC,两线的交点为O,
∵四边形BCKN是正方形,
∴∠NOB=90°,OB=ON,
∵BN=4cm,
∴由勾股定理得:BO=ON=2cm,
∵JN=2cm,
∴AM=JO=(2+2)cm;
(2)如图,作小正方形的对角线,组成正方形ORZQ,
则正方形的边长为(2+4+2)cm,即为(4+4)cm,
所以正八边形CDEFGHIK的面积为S正方形OQZR﹣4S△BOC=(4+4)2﹣4××2×2=(32+32)cm2;
(3)正方形地砖的边长为:2×(2+2)cm+(4+4)cm=(8+8)cm,
∵3.14米=314cm,
∴3142÷(8+8)2≈264,
∵162<264,
∴用该地砖铺设完毕后,最多形成32×32=1024个正八边形.
23.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∵AE=CF.
∴BE=FD,BE∥FD,
∴四边形EBFD是平行四边形,
∴DE=BF.
24.解:(1)∵DE⊥AB于E,且E为AB的中点,
∴AD=BD,
∵四边形ABCD是菱形,
∴AD=BA,
∴AB=AD=BD,
∴△ABD是等边三角形,
∴∠DAB=60°;
(2)∵BD=4,△ABD是等边三角形,
∴DO=2,AD=4,
∴AO==2,
∴AC=4;
(3)菱形ABCD的面积为:
BD?AC=×4×4=8.
25.证明:∵AD是△ABC的角平分线,∴∠EAD=∠FAD,
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,∠EAD=∠ADF,
∴∠FAD=∠FDA
∴AF=DF,
∴四边形AEDF是菱形.
26.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAE.
∵AD⊥BD,
∴∠ADB=∠ADE=90°.
在△ADB与△ADE中,
∴△ADB≌△ADE,
∴BD=DE.
(2)∵△ADB≌△ADE,
∴AE=AB=12,
∴EC=AC﹣AE=8.
∵M是BC的中点,BD=DE,
∴DM=EC=4.
四边形》单元测试卷
一.选择题
1.如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
A.3cm
B.6cm
C.9cm
D.12cm
2.四边形具有不稳定性,对于四条边长确定的四边形.当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′.若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )
A.1
B.
C.
D.
3.某人到瓷砖商店去买一种多边形形状的瓷砖用来铺设无缝地板,他购买的瓷砖形状不可以是( )
A.正三角形
B.长方形
C.正八边形
D.正六边形
4.下面性质中,平行四边形不一定具备的是( )
A.对角互补
B.邻角互补
C.对角相等
D.对角线互相平分
5.如果n边形的内角和是它外角和的4倍,则n等于( )
A.7
B.8
C.10
D.9
6.如果过一个多边形的一个顶点的对角线有6条,则该多边形是( )
A.九边形
B.八边形
C.七边形
D.六边形
7.对角线互相垂直且相等的四边形是( )
A.菱形
B.矩形
C.正方形
D.以上结论都不对
8.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A.20cm
B.30cm
C.40cm
D.20cm
9.下列说法中不正确的是( )
A.四边相等的四边形是菱形
B.对角线垂直的平行四边形是菱形
C.菱形的对角线互相垂直且相等
D.菱形的邻边相等
10.下列结论中,菱形具有而矩形不一定具有的性质是( )
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对边相等且平行
二.填空题
11.一个多边形的每个外角都是40°,则这个多边形的内角和是
.
12.如图所示,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的对角线AC的长是
.
13.四边形具有不稳定性.如图,矩形ABCD按箭头方向变形成平行四边形A'B'C'D',当变形后图形面积是原图形面积的一半时,则∠A'=
.
14.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是
.
15.把边长为a的正三角形和正方形组合镶嵌,若用2个正方形,则还需
个正三角形才可以镶嵌.
16.菱形ABCD中,若周长是20cm,对角线AC=6cm,则对角线BD=
cm.
17.过多边形的某一个顶点的所有对角线可以把多边形分成5个三角形,则这个多边形是
边形.
18.如图,过平行四边形ABCD的对角找BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是
.
19.如图,下列条件之一能使?ABCD是菱形的有
(填序号)
①AC⊥BD;
②∠BAD=90°;
③AB=BC;
④AC=BD.
20.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则BD的长为
.
三.解答题
21.在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
22.小明家准备装修厨房,打算铺设如图1的正方形地砖,该地砖既是轴对称图形也是中心对称图形,铺设效果如图2所示.经测量图1发现,砖面上四个小正方形的边长都是4cm,AB=JN=2cm,中间的多边形CDEFGHIK是正八边形.
(1)求MA的长度;
(2)求正八边形CDEFGHIK的面积;
(3)已知小明家厨房的地面是边长为3.14米的正方形,用该地砖铺设完毕后,最多形成多少个正八边形?(地砖间缝隙的宽度忽略不计)
23.在?ABCD中,点E、F分别在AB、CD上,且AE=CF.求证:DE=BF.
24.已知,如图,菱形ABCD,DE⊥AB于E,且E为AB的中点,已知BD=4.
(1)∠DAB的度数;
(2)AC的长;
(3)菱形ABCD的面积.
25.如图,在△ABC中,AD平分∠BAC,DE∥AC,DF∥AB.求证:四边形AEDF是菱形.
26.在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.
(1)求证:BD=DE;
(2)求DM的长.
参考答案与试题解析
一.选择题
1.解:∵四边形ABCD是平行四边形,
∴OA=OC;
又∵点E是BC的中点,
∴BE=CE,
∴AB=2OE=2×3=6(cm)
故选:B.
2.解:根据题意可知菱形ABC′D′的高等于AB的一半,
∴菱形ABC′D′的面积为,正方形ABCD的面积为AB2.
∴菱形ABC′D′的面积与正方形ABCD的面积之比是.
故选:B.
3.解;A、正三角形的内角是60°,6个正三角形可以密铺,故A可以;
B、长方形的内角是90°,4个长方形可以密铺,故B可以;
C、正八边形的内角是135°,2个正八边形有缝隙,3个正八边形重叠,故C不可以;
D、正六边形的内角是120°,3个正六边形可以密铺,故D可以;
故选:C.
4.解:∵平行四边形的对角相等,对角线互相平分,对边平行,即可得平行四边形的邻角互补;
∴B、C、D正确.
故选:A.
5.解:多边形的外角和是360°,根据题意得:
180°?(n﹣2)=360°×4,
解得n=10.
故选:C.
6.解:∵过一个多边形的一个顶点的对角线有6条,
∴多边形的边数为6+3=9,
∴这个多边形是九边形.
故选:A.
7.解:对角线互相垂直且相等,但不互相平分的四边形不是菱形、矩形、正方形,因为这三种四边形的对角线都互相平分.
故选:D.
8.解:如图1,图2中,连接AC.
图1中,∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC是等边三角形,
∴AB=BC=AC=20cm,
在图2中,∵四边形ABCD是正方形,
∴AB=BC,∠B=90°,
∴△ABC是等腰直角三角形,
∴AC=AB=20cm;
故选:D.
9.解:A.四边相等的四边形是菱形;正确;
B.对角线垂直的平行四边形是菱形;正确;
C.菱形的对角线互相垂直且相等;不正确;
D.菱形的邻边相等;正确;
故选:C.
10.解:A.因为矩形的对角线相等,所以A选项不符合题意;
B.因为矩形和菱形的对角线都互相平分,所以B选项不符合题意;
C.因为菱形对角线互相垂直,所以C选项符合题意;
D.因为矩形和菱形的对边都相等且平行,不符合题意.
故选:C.
二.填空题
11.解:设多边形的边数为n,
∵多边形的每个外角都等于40°,
∴n=360÷40=9,
∴这个多边形的内角和=(9﹣2)×180°=1260°.
故答案为1260°.
12.解:∵四边形ABCD是矩形,
∴AC=2AO,BD=2BO,AC=BD,
∴AO=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO=2,
即AC=2AO=4,
故答案为:4.
13.解:∵,
∴平行四边形A'B'C'D'的底边A′D′边上的高等于A′B′的一半,
∴∠A'=30°.
故答案为:30°
14.解:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PF=BC,PE=AD,又AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=30°,
∴∠EPF=120°,
故答案为:120°.
15.解:∵正三角形的每个内角是60°,正方形的每个内角是90°,
又∵3×60°+2×90°=360°,
∴用2个正方形,则还需3个正三角形才可以镶嵌.
故答案为:3.
16.解:如图,∵菱形ABCD的周长是20cm,对角线AC=6cm,
∴AB=20÷4=5cm,AO=AC=3cm,
又∵AC⊥BD,
∴BO===4cm,
∴BD=2BO=8cm.
故答案为:8.
17.解:设多边形有n条边,
则n﹣2=5,
解得n=7.
故这个多边形是七边形.
故答案为:七.
18.解:∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2.
故答案为:S1=S2.
19.解:因为一组邻边相等的平行四边形是菱形;对角线互相垂直平分的四边形是菱形.则能使?ABCD是菱形的有①或③.
20.解:过点A作AE⊥BC于E,AF⊥CD于F,
∵两条纸条宽度相同,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵S?ABCD=BC?AE=CD?AF.
又∵AE=AF.
∴BC=CD,
∴四边形ABCD是菱形,
连接AC,BD相交于点O,
∴AC⊥BD,AO=AC=1,
∴BO==2,
∴BD=2BO=4,
故答案为:4.
三.解答题
21.解:(1)设多边形的一个外角为α,则与其相邻的内角等于3α+20°,
由题意,得(3α+20)+α=180°,解得α=40°.
即多边形的每个外角为40°.
又∵多边形的外角和为360°,
∴多边形的外角个数==9.
∴多边形的边数=9,
答:这个多边形的边数是9;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
当截线为经过对角2个顶点的直线时,多边形的边数减少了1条边,内角和=(9﹣2﹣1)×180°=1080°;
当截线为经过多边形一组对边的直线时,多边形的边数不变,内角和=(9﹣2)×180°=1260°;
当截线为只经过正方形一组邻边的一条直线时,多边形的边数增加一条边,内角和=(9﹣2+1)×180°=1440°.
答:将这个多边形剪去一个角,剩下多边形的内角和是1080°或1260°或1440°.
22.解:(1)连接BK和NC,两线的交点为O,
∵四边形BCKN是正方形,
∴∠NOB=90°,OB=ON,
∵BN=4cm,
∴由勾股定理得:BO=ON=2cm,
∵JN=2cm,
∴AM=JO=(2+2)cm;
(2)如图,作小正方形的对角线,组成正方形ORZQ,
则正方形的边长为(2+4+2)cm,即为(4+4)cm,
所以正八边形CDEFGHIK的面积为S正方形OQZR﹣4S△BOC=(4+4)2﹣4××2×2=(32+32)cm2;
(3)正方形地砖的边长为:2×(2+2)cm+(4+4)cm=(8+8)cm,
∵3.14米=314cm,
∴3142÷(8+8)2≈264,
∵162<264,
∴用该地砖铺设完毕后,最多形成32×32=1024个正八边形.
23.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∵AE=CF.
∴BE=FD,BE∥FD,
∴四边形EBFD是平行四边形,
∴DE=BF.
24.解:(1)∵DE⊥AB于E,且E为AB的中点,
∴AD=BD,
∵四边形ABCD是菱形,
∴AD=BA,
∴AB=AD=BD,
∴△ABD是等边三角形,
∴∠DAB=60°;
(2)∵BD=4,△ABD是等边三角形,
∴DO=2,AD=4,
∴AO==2,
∴AC=4;
(3)菱形ABCD的面积为:
BD?AC=×4×4=8.
25.证明:∵AD是△ABC的角平分线,∴∠EAD=∠FAD,
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,∠EAD=∠ADF,
∴∠FAD=∠FDA
∴AF=DF,
∴四边形AEDF是菱形.
26.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAE.
∵AD⊥BD,
∴∠ADB=∠ADE=90°.
在△ADB与△ADE中,
∴△ADB≌△ADE,
∴BD=DE.
(2)∵△ADB≌△ADE,
∴AE=AB=12,
∴EC=AC﹣AE=8.
∵M是BC的中点,BD=DE,
∴DM=EC=4.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
