2020-2021学年湘教新版九年级下册数学《第2章 圆》单元复习卷(word版,有答案)
文档属性
| 名称 | 2020-2021学年湘教新版九年级下册数学《第2章 圆》单元复习卷(word版,有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 353.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-27 17:18:43 | ||
图片预览




文档简介
2020-2021学年湘教新版九年级下册数学《第2章
圆》单元测试卷
一.选择题
1.A、B是半径为5cm的⊙O上两个不同的点,则弦AB的取值范围是( )
A.AB>0
B.0<AB<5
C.0<AB<10
D.0<AB≤10
2.如图,⊙O中,ABDC是圆内接四边形,∠BOC=110°,则∠BDC的度数是( )
A.110°
B.70°
C.55°
D.125°
3.已知⊙O的直径为10,点P到点O的距离大于8,那么点P的位置( )
A.一定在⊙O的内部
B.一定在⊙O的外部
C.一定在⊙O上
D.不能确定
4.下列各说法中:
①圆的每一条直径都是它的对称轴;
②长度相等的两条弧是等弧;
③相等的弦所对的弧也相等;
④同弧所对的圆周角相等;
⑤90°的圆周角所对的弦是直径;
⑥任何一个三角形都有唯一的外接圆;
其中正确的有( )
A.3个
B.4个
C.5个
D.6个
5.已知⊙O的直径为4,点O到直线l的距离为2,则直线l与⊙O的位置关系是( )
A.相交
B.相切
C.相离
D.无法判断
6.如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.
cm
B.8cm
C.6cm
D.4cm
7.如图,半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
A.10cm
B.16cm
C.24cm
D.26cm
8.如图,AB为⊙O的直径,∠BED=40°,则∠ACD的度数为( )
A.90°
B.50°
C.45°
D.80°
9.如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
A.45°
B.60°
C.45°
或135°
D.60°
或120°
10.如图,设AD,BE,CF为三角形ABC的三条高,若AB=6,BC=5,EF=3,则线段BE的长为( )
A.
B.4
C.
D.
二.填空题
11.如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O半径为
.
12.在直径为200cm的圆柱形油箱内装入一些油以后,截面如图(油面在圆心下):若油面的宽AB=160cm,则油的最大深度为
.
13.已知弦AB的长等于⊙O的半径,弦AB所对的圆周角是
度.
14.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D是半径为4的⊙A上一动点,点M是CD的中点,则BM的最大值是
.
15.如图,⊙O的弦AB、CD相交于点E,若CE:BE=2:3,则AE:DE=
.
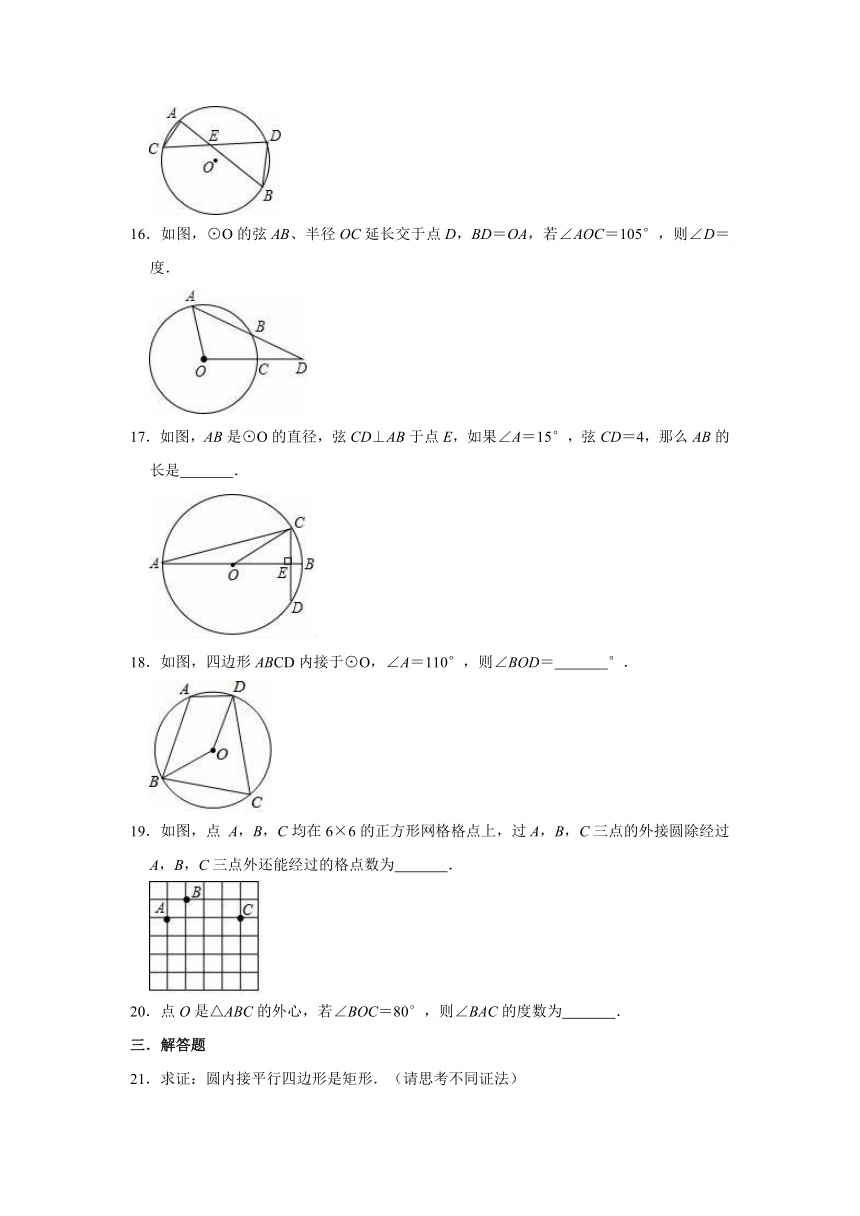
16.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D=
度.
17.如图,AB是⊙O的直径,弦CD⊥AB于点E,如果∠A=15°,弦CD=4,那么AB的长是
.
18.如图,四边形ABCD内接于⊙O,∠A=110°,则∠BOD=
°.
19.如图,点
A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为
.
20.点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为
.
三.解答题
21.求证:圆内接平行四边形是矩形.(请思考不同证法)
22.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
23.如图,四边形ABCD内接于⊙O,OC=4,AC=4.
(1)求点O到AC的距离;
(2)求∠ADC的度数.
24.木工师傅可以用角尺测量并计算出圆的半径r.用角尺的较短边紧靠⊙O,角尺的顶点B(∠B=90°),并使较长边与⊙O相切于点C.
(1)如图,AB<r,较短边AB=8cm,读得BC长为12cm,则该圆的半径r为多少?
(2)如果AB=8cm,假设角尺的边BC足够长,若读得BC长为acm,则用含a的代数式表示r为
.
25.已知P是⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP.若∠APQ=∠BPQ.
(1)如图1,当∠APQ=45°,AP=1,BP=2时,求⊙O的半径;
(2)如图2,连接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若∠NOP+2∠OPN=90°,探究直线AB与ON的位置关系,并证明.
26.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=6,AC=8,求⊙O的半径及CE的长.
27.如图,一段圆弧与长度为1的正方形网格的交点是A、B、C.
(1)请完成以下操作:
①以点O为原点,垂直和水平方向为轴,网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD;
(2)请在(1)的基础上,完成下列填空:
⊙D的半径=
(结果保留根号).点(7,0)在⊙D
;(填“上”、“内”、“外”)
③∠ADC的度数为
.
参考答案与试题解析
一.选择题
1.解:∵圆中最长的弦为直径,
∴0<AB≤10.
故选:D.
2.解:∵∠BOC=110°
∴∠A=∠BOC=×110°=55°
又∵ABDC是圆内接四边形
∴∠A+∠D=180°
∴∠D=180°﹣55°=125°
故选:D.
3.解:r=×10=5,
d=8>r,
点P一定在⊙O的外部.
故选:B.
4.解:①对称轴是直线,而直径是线段,圆的每一条直径所在直线都是它的对称轴,所以此项错误;
②在同一圆中,长度相等的两条弧是等弧,不在同一圆中不一定是等弧,所以此项错误;
③在同一圆中,相等的弦所对的弧也相等,不在同一圆中,相等的弦所对的弧不一定相等,所以此项错误;
④根据圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,故此项正确;
⑤根据圆周角定理推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径,故此项正确;
⑥根据三角形外接圆的定义可知,任何一个三角形都有唯一的外接圆,故此项正确.
故选:A.
5.解:∵⊙O的直径为4,
∴⊙O的半径为2,
∵点O到直线l的距离为2,
∴d=r
∴l与⊙O的位置关系相切.
故选:B.
6.解:如图所示,连接OA.
⊙O的直径CD=10cm,
则⊙O的半径为5cm,
即OA=OC=5,
又∵OM:OC=3:5,
所以OM=3,
∵AB⊥CD,垂足为M,
∴AM=BM,
在Rt△AOM中,AM==4,
∴AB=2AM=2×4=8.
故选:B.
7.解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=8cm,OD=13cm,
∴OC=5cm,
又∵OB=13cm,
∴Rt△BCO中,BC==12cm,
∴AB=2BC=24cm.
故选:C.
8.解:连接AE,
∵AB为直径,
∴∠AEB=90°,
∴∠AED=90°﹣40°=50°,
∴∠ACD=∠AED=50°.
故选:B.
9.解:连接OA,OB,
∵⊙O是正方形ABCD的外接圆,
∴∠AOB=90°,
若点P在优弧ADB上,则∠APB=∠AOB=45°;
若点P在劣弧AB上,
则∠APB=180°﹣45°=135°.
∴∠APB=45°或135°.
故选:C.
10.解:∵AD,BE,CF为△ABC的三条高,易知B,C,E,F四点共圆
∴△AEF∽△ABC
∴,即cos∠BAC=
∴sin∠BAC=
∴在Rt△ABE中,BE=AB?sin∠BAC=6=.
故选:D.
二.填空题
11.解:连接OC,设⊙O半径为r,则OC=r,OE=r﹣BE=r﹣2,
∵CD⊥AB,
∴CE=DE=CD=6,
在Rt△OCE中,∵OE2+CE2=OC2,
∴(r﹣2)2+62=r2,解得r=10,
即⊙O半径为10.
故答案为10.
12.40cm解:连接OA,过点O作OE⊥AB,交AB于点M,
∵直径为200cm,AB=160cm,
∴OA=OE=100cm,AM=80cm,
∴OM===60cm,
∴ME=OE﹣OM=100﹣60=40cm.
故答案为40cm.
13.解:如图示,AB=OA=OB,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴∠ACB=30°,
∴∠ADB=150°.
故弦AB所对的圆周角是
30或150度.
故答案为:30或150.
14.解:如图,取AC的中点N,连接MN,BN.
∵∠ABC=90°,AB=8,BC=6,
∴AC=10,
∵AN=NC,
∴BN=AC=5,
∵AN=NC,DM=MC,
∴MN==2,
∴BM≤BN+NM,
∴BM≤5+2=7,
即BM的最大值是7.
故答案为7.
15.解:∵⊙O的弦AB、CD相交于点E,
∴AE?BE=CE?DE,
∴AE:DE=CE:BE=2:3,
故答案为:2:3.
16.解:连接OB,
∵BD=OA,OA=OB
所以△AOB和△BOD为等腰三角形,
设∠D=x度,则∠OBA=2x°,
因为OB=OA,
所以∠A=2x°,
在△AOB中,2x+2x+(105﹣x)=180,
解得x=25,
即∠D=25°.
17.解:∵∠A=15°,
∴∠COB=30°,
∵AB是⊙O的直径,弦CD⊥AB于点E,弦CD=4,
∴CE=2,∠OEC=90°
∵∠COE=30°,
∴OC=2CE=4,
∴AB=2OC=8,
故答案为:8
18.解:∵四边形ABCD内接于⊙O,∠A=110°,
∴∠C=180°﹣∠A=180°﹣110°=70°,
∴∠BOD=2∠C=140°.
故答案为:140.
19.解:如图,分别作AB、BC的中垂线,两直线的交点为O,
以O为圆心、OA为半径作圆,则⊙O即为过A,B,C三点的外接圆,
由图可知,⊙O还经过点D、E、F、G、H这5个格点,
故答案为:5.
20.解:如图所示:
∵O是△ABC的外心,∠BOC=80°,
∴∠A=40°,
∠A′=180°﹣∠A=140°,
故∠BAC的度数为:40°或140°
故答案为:40°或140°.
三.解答题
21.已知:平行四边形ABCD是⊙O的内接四边形,
求证:四边形ABCD是矩形,
证明:方法一、∵平行四边形ABCD是⊙O的内接四边形,
∴∠B=∠D,∠B+∠D=180°,
∴∠B=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
方法二、∵∠B=∠D=90°,
同理∠A=∠C=90°,
∴四边形ABCD是矩形(有三个角是直角的四边形是矩形).
22.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
23.解:(1)作OM⊥AC于M,
∵AC=4,
∴AM=CM=2,
∵OC=4,
∴OM==2;
(2)连接OA,
∵OM=MC,∠OMC=90°,
∴∠MOC=∠MCO=45°,
∵OA=OC,
∴∠OAM=45°,
∴∠AOC=90°,
∴∠B=45°,
∵∠D+∠B=180°,
∴∠D=135°.
24.解:(1)如图1,连接OC、OA,作AD⊥OC,垂足为D.则OD=r﹣8
在Rt△AOD中,r2=(r﹣8)2+122
解得:r=13;
答:该圆的半径r为13;
(2)①如图2,易知,0<r≤8时,r=a;
②当r>8时,
如图1:连接OC,连接OA,过点A作AD⊥OC于点D,
∵BC与⊙O相切于点C,
∴OC⊥BC,
则四边形ABCD是矩形,即AD=BC,CD=AB.
在Rt△AOD中,OA2=OD2+AD2,
即:r2=(r﹣8)2+a2,
整理得:r=a2+4.
故答案为:0<r≤8时,r=a;当r>8时,r=a
2+4.
25.解:(1)连接AB,
∵∠APQ=∠BPQ=45°,
∴∠APB=∠APQ+BPQ=90°,
∴AB是⊙O的直径,
∴AB===3,
∴⊙O的半径为;
(2)AB∥ON,
证明:连接OA、OB、OQ,
∵∠APQ=∠BPQ,
∴=,
∴∠AOQ=∠BOQ,
∵OA=OB,
∴OQ⊥AB,
∵OP=OQ,
∴∠OPN=∠OQP,
∵∠OPN+∠OQP+∠PON+∠NOQ=180°,
∴2∠OPN+∠PON+∠NOQ=180°,
∵∠NOP+2∠OPN=90°,
∴∠NOQ=90°,
∴NO⊥OQ,
∴AB∥ON.
26.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A=90°﹣∠ABC.
∵CE⊥AB,
∴∠CEB=90°,
∴∠ECB=90°﹣∠ABC,
∴∠ECB=∠A.(2分)
又∵C是的中点,
∴=,
∴∠DBC=∠A,
∴∠ECB=∠DBC,
∴CF=BF;
(2)解:∵=,
∴BC=CD=6,
∵∠ACB=90°,
∴AB===10,
∴⊙O的半径为5,
∵S△ABC=AB?CE=BC?AC,
∴CE===.
27.解:(1)如图1所示:
;
(2)⊙D的半径为:=2,∵OD=2,
∴7﹣2=5>2,
∴(7,0)在⊙D外,
故答案为:2;外;
③∵OA=DF=4,CF=OD=2,∠AOD=∠DFC=90°,
∴在△AOD和△DFC中
,
∴△AOD≌△DFC(SAS),
∴∠OAD=∠CDF,
∵∠AOD=90°,
∴∠ADC=180°﹣(∠ADO+∠CDF)
=180°﹣(∠ADO+∠OAD)
=∠AOD
=90°,
故答案为:90°.
圆》单元测试卷
一.选择题
1.A、B是半径为5cm的⊙O上两个不同的点,则弦AB的取值范围是( )
A.AB>0
B.0<AB<5
C.0<AB<10
D.0<AB≤10
2.如图,⊙O中,ABDC是圆内接四边形,∠BOC=110°,则∠BDC的度数是( )
A.110°
B.70°
C.55°
D.125°
3.已知⊙O的直径为10,点P到点O的距离大于8,那么点P的位置( )
A.一定在⊙O的内部
B.一定在⊙O的外部
C.一定在⊙O上
D.不能确定
4.下列各说法中:
①圆的每一条直径都是它的对称轴;
②长度相等的两条弧是等弧;
③相等的弦所对的弧也相等;
④同弧所对的圆周角相等;
⑤90°的圆周角所对的弦是直径;
⑥任何一个三角形都有唯一的外接圆;
其中正确的有( )
A.3个
B.4个
C.5个
D.6个
5.已知⊙O的直径为4,点O到直线l的距离为2,则直线l与⊙O的位置关系是( )
A.相交
B.相切
C.相离
D.无法判断
6.如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.
cm
B.8cm
C.6cm
D.4cm
7.如图,半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB的长为( )
A.10cm
B.16cm
C.24cm
D.26cm
8.如图,AB为⊙O的直径,∠BED=40°,则∠ACD的度数为( )
A.90°
B.50°
C.45°
D.80°
9.如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
A.45°
B.60°
C.45°
或135°
D.60°
或120°
10.如图,设AD,BE,CF为三角形ABC的三条高,若AB=6,BC=5,EF=3,则线段BE的长为( )
A.
B.4
C.
D.
二.填空题
11.如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O半径为
.
12.在直径为200cm的圆柱形油箱内装入一些油以后,截面如图(油面在圆心下):若油面的宽AB=160cm,则油的最大深度为
.
13.已知弦AB的长等于⊙O的半径,弦AB所对的圆周角是
度.
14.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D是半径为4的⊙A上一动点,点M是CD的中点,则BM的最大值是
.
15.如图,⊙O的弦AB、CD相交于点E,若CE:BE=2:3,则AE:DE=
.
16.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D=
度.
17.如图,AB是⊙O的直径,弦CD⊥AB于点E,如果∠A=15°,弦CD=4,那么AB的长是
.
18.如图,四边形ABCD内接于⊙O,∠A=110°,则∠BOD=
°.
19.如图,点
A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为
.
20.点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为
.
三.解答题
21.求证:圆内接平行四边形是矩形.(请思考不同证法)
22.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
23.如图,四边形ABCD内接于⊙O,OC=4,AC=4.
(1)求点O到AC的距离;
(2)求∠ADC的度数.
24.木工师傅可以用角尺测量并计算出圆的半径r.用角尺的较短边紧靠⊙O,角尺的顶点B(∠B=90°),并使较长边与⊙O相切于点C.
(1)如图,AB<r,较短边AB=8cm,读得BC长为12cm,则该圆的半径r为多少?
(2)如果AB=8cm,假设角尺的边BC足够长,若读得BC长为acm,则用含a的代数式表示r为
.
25.已知P是⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP.若∠APQ=∠BPQ.
(1)如图1,当∠APQ=45°,AP=1,BP=2时,求⊙O的半径;
(2)如图2,连接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若∠NOP+2∠OPN=90°,探究直线AB与ON的位置关系,并证明.
26.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=6,AC=8,求⊙O的半径及CE的长.
27.如图,一段圆弧与长度为1的正方形网格的交点是A、B、C.
(1)请完成以下操作:
①以点O为原点,垂直和水平方向为轴,网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD;
(2)请在(1)的基础上,完成下列填空:
⊙D的半径=
(结果保留根号).点(7,0)在⊙D
;(填“上”、“内”、“外”)
③∠ADC的度数为
.
参考答案与试题解析
一.选择题
1.解:∵圆中最长的弦为直径,
∴0<AB≤10.
故选:D.
2.解:∵∠BOC=110°
∴∠A=∠BOC=×110°=55°
又∵ABDC是圆内接四边形
∴∠A+∠D=180°
∴∠D=180°﹣55°=125°
故选:D.
3.解:r=×10=5,
d=8>r,
点P一定在⊙O的外部.
故选:B.
4.解:①对称轴是直线,而直径是线段,圆的每一条直径所在直线都是它的对称轴,所以此项错误;
②在同一圆中,长度相等的两条弧是等弧,不在同一圆中不一定是等弧,所以此项错误;
③在同一圆中,相等的弦所对的弧也相等,不在同一圆中,相等的弦所对的弧不一定相等,所以此项错误;
④根据圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,故此项正确;
⑤根据圆周角定理推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径,故此项正确;
⑥根据三角形外接圆的定义可知,任何一个三角形都有唯一的外接圆,故此项正确.
故选:A.
5.解:∵⊙O的直径为4,
∴⊙O的半径为2,
∵点O到直线l的距离为2,
∴d=r
∴l与⊙O的位置关系相切.
故选:B.
6.解:如图所示,连接OA.
⊙O的直径CD=10cm,
则⊙O的半径为5cm,
即OA=OC=5,
又∵OM:OC=3:5,
所以OM=3,
∵AB⊥CD,垂足为M,
∴AM=BM,
在Rt△AOM中,AM==4,
∴AB=2AM=2×4=8.
故选:B.
7.解:如图,过O作OD⊥AB于C,交⊙O于D,
∵CD=8cm,OD=13cm,
∴OC=5cm,
又∵OB=13cm,
∴Rt△BCO中,BC==12cm,
∴AB=2BC=24cm.
故选:C.
8.解:连接AE,
∵AB为直径,
∴∠AEB=90°,
∴∠AED=90°﹣40°=50°,
∴∠ACD=∠AED=50°.
故选:B.
9.解:连接OA,OB,
∵⊙O是正方形ABCD的外接圆,
∴∠AOB=90°,
若点P在优弧ADB上,则∠APB=∠AOB=45°;
若点P在劣弧AB上,
则∠APB=180°﹣45°=135°.
∴∠APB=45°或135°.
故选:C.
10.解:∵AD,BE,CF为△ABC的三条高,易知B,C,E,F四点共圆
∴△AEF∽△ABC
∴,即cos∠BAC=
∴sin∠BAC=
∴在Rt△ABE中,BE=AB?sin∠BAC=6=.
故选:D.
二.填空题
11.解:连接OC,设⊙O半径为r,则OC=r,OE=r﹣BE=r﹣2,
∵CD⊥AB,
∴CE=DE=CD=6,
在Rt△OCE中,∵OE2+CE2=OC2,
∴(r﹣2)2+62=r2,解得r=10,
即⊙O半径为10.
故答案为10.
12.40cm解:连接OA,过点O作OE⊥AB,交AB于点M,
∵直径为200cm,AB=160cm,
∴OA=OE=100cm,AM=80cm,
∴OM===60cm,
∴ME=OE﹣OM=100﹣60=40cm.
故答案为40cm.
13.解:如图示,AB=OA=OB,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴∠ACB=30°,
∴∠ADB=150°.
故弦AB所对的圆周角是
30或150度.
故答案为:30或150.
14.解:如图,取AC的中点N,连接MN,BN.
∵∠ABC=90°,AB=8,BC=6,
∴AC=10,
∵AN=NC,
∴BN=AC=5,
∵AN=NC,DM=MC,
∴MN==2,
∴BM≤BN+NM,
∴BM≤5+2=7,
即BM的最大值是7.
故答案为7.
15.解:∵⊙O的弦AB、CD相交于点E,
∴AE?BE=CE?DE,
∴AE:DE=CE:BE=2:3,
故答案为:2:3.
16.解:连接OB,
∵BD=OA,OA=OB
所以△AOB和△BOD为等腰三角形,
设∠D=x度,则∠OBA=2x°,
因为OB=OA,
所以∠A=2x°,
在△AOB中,2x+2x+(105﹣x)=180,
解得x=25,
即∠D=25°.
17.解:∵∠A=15°,
∴∠COB=30°,
∵AB是⊙O的直径,弦CD⊥AB于点E,弦CD=4,
∴CE=2,∠OEC=90°
∵∠COE=30°,
∴OC=2CE=4,
∴AB=2OC=8,
故答案为:8
18.解:∵四边形ABCD内接于⊙O,∠A=110°,
∴∠C=180°﹣∠A=180°﹣110°=70°,
∴∠BOD=2∠C=140°.
故答案为:140.
19.解:如图,分别作AB、BC的中垂线,两直线的交点为O,
以O为圆心、OA为半径作圆,则⊙O即为过A,B,C三点的外接圆,
由图可知,⊙O还经过点D、E、F、G、H这5个格点,
故答案为:5.
20.解:如图所示:
∵O是△ABC的外心,∠BOC=80°,
∴∠A=40°,
∠A′=180°﹣∠A=140°,
故∠BAC的度数为:40°或140°
故答案为:40°或140°.
三.解答题
21.已知:平行四边形ABCD是⊙O的内接四边形,
求证:四边形ABCD是矩形,
证明:方法一、∵平行四边形ABCD是⊙O的内接四边形,
∴∠B=∠D,∠B+∠D=180°,
∴∠B=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
方法二、∵∠B=∠D=90°,
同理∠A=∠C=90°,
∴四边形ABCD是矩形(有三个角是直角的四边形是矩形).
22.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
23.解:(1)作OM⊥AC于M,
∵AC=4,
∴AM=CM=2,
∵OC=4,
∴OM==2;
(2)连接OA,
∵OM=MC,∠OMC=90°,
∴∠MOC=∠MCO=45°,
∵OA=OC,
∴∠OAM=45°,
∴∠AOC=90°,
∴∠B=45°,
∵∠D+∠B=180°,
∴∠D=135°.
24.解:(1)如图1,连接OC、OA,作AD⊥OC,垂足为D.则OD=r﹣8
在Rt△AOD中,r2=(r﹣8)2+122
解得:r=13;
答:该圆的半径r为13;
(2)①如图2,易知,0<r≤8时,r=a;
②当r>8时,
如图1:连接OC,连接OA,过点A作AD⊥OC于点D,
∵BC与⊙O相切于点C,
∴OC⊥BC,
则四边形ABCD是矩形,即AD=BC,CD=AB.
在Rt△AOD中,OA2=OD2+AD2,
即:r2=(r﹣8)2+a2,
整理得:r=a2+4.
故答案为:0<r≤8时,r=a;当r>8时,r=a
2+4.
25.解:(1)连接AB,
∵∠APQ=∠BPQ=45°,
∴∠APB=∠APQ+BPQ=90°,
∴AB是⊙O的直径,
∴AB===3,
∴⊙O的半径为;
(2)AB∥ON,
证明:连接OA、OB、OQ,
∵∠APQ=∠BPQ,
∴=,
∴∠AOQ=∠BOQ,
∵OA=OB,
∴OQ⊥AB,
∵OP=OQ,
∴∠OPN=∠OQP,
∵∠OPN+∠OQP+∠PON+∠NOQ=180°,
∴2∠OPN+∠PON+∠NOQ=180°,
∵∠NOP+2∠OPN=90°,
∴∠NOQ=90°,
∴NO⊥OQ,
∴AB∥ON.
26.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A=90°﹣∠ABC.
∵CE⊥AB,
∴∠CEB=90°,
∴∠ECB=90°﹣∠ABC,
∴∠ECB=∠A.(2分)
又∵C是的中点,
∴=,
∴∠DBC=∠A,
∴∠ECB=∠DBC,
∴CF=BF;
(2)解:∵=,
∴BC=CD=6,
∵∠ACB=90°,
∴AB===10,
∴⊙O的半径为5,
∵S△ABC=AB?CE=BC?AC,
∴CE===.
27.解:(1)如图1所示:
;
(2)⊙D的半径为:=2,∵OD=2,
∴7﹣2=5>2,
∴(7,0)在⊙D外,
故答案为:2;外;
③∵OA=DF=4,CF=OD=2,∠AOD=∠DFC=90°,
∴在△AOD和△DFC中
,
∴△AOD≌△DFC(SAS),
∴∠OAD=∠CDF,
∵∠AOD=90°,
∴∠ADC=180°﹣(∠ADO+∠CDF)
=180°﹣(∠ADO+∠OAD)
=∠AOD
=90°,
故答案为:90°.
