2020-2021学年高中数学必修5第二章2.4.1等比数列(第一课时)课件(共19张PPT)
文档属性
| 名称 | 2020-2021学年高中数学必修5第二章2.4.1等比数列(第一课时)课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 744.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 18:41:42 | ||
图片预览






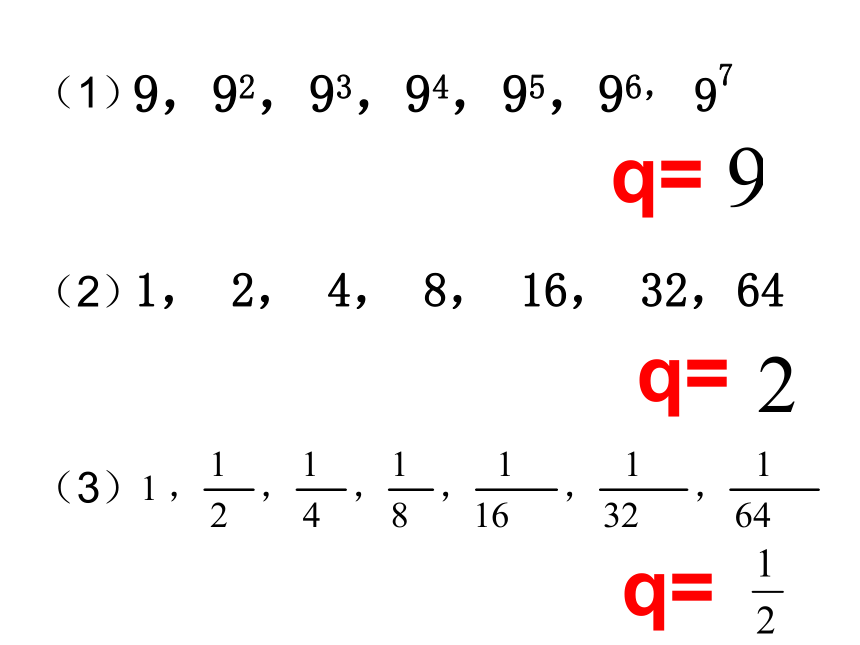
文档简介
一、复习与回顾
等差数列:
定义
递推公式
通项公式
等差中项
前n项和Sn
2.4
出门见九堤,每堤有九木,每木有九巢,每巢有九鸟,每鸟有九雏,每雏有九毛,每毛有九色,问共有几堤,几木,几巢,几鸟,几雏,几毛,几色?(《孙子算经》)
堤、木,巢、鸟、雏、毛、色依次构成数列:
9,92,93,94,95,96, 97
“一尺之棰,日取其半,万世不竭”
——(《庄子》)
我们得到这样一组数:
已知某种细胞每分钟分裂一次,随着时间变化我们得到下面这组数:
1,2,4,8,16,32,……
(1)
9,92,93,94,95,96, 97
(3)
(2)
1, 2, 4, 8, 16, 32,……
有什么共同特征?
(1)
9,92,93,94,95,96, 97
(2)
(3)
1, 2, 4, 8, 16, 32,64
q=
q=
q=
等差数列:
如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,常用字母d表示(d∈R)。
等比数列:
如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,常用字母q表示(q≠0)。
判断数列{an}是等比数列的依据
下面的例子中哪些是等比数列?
① 3,6,12,24,48,……
② 0,0,0,0,0,0,……
③3,3,3,3,3,3,……
④2,-4,8,-16,32,……
是
不是
是
是
二、通项公式
……
1.递推法
二、通项公式
……
共计
n-1项
2.累乘法
【即时训练】
在等比数列{an}中,a1=2,q=3,求通项公式an。
【例1】在等比数列{an}中,
a2=18,a4=8,求a1和q.
【例2】一个等比数列的
第三项和第四项分别是12和18,
求它的第一项和第二项。
三、等比中项
如果a和b之间一个数G,
a、G和b成等比数列,那么G叫做a与b的等比中项,
这三个数满足关系式ab=G2
【例3】若三个正数a、b和c成等比数列,其中a= ,c= ,求b.
【例4】若a,2a+2,3a+3成等比数列,求实数a的值.
课堂小结:类比等差数列
1.等比数列定义
2.递推公式
3.通项公式
4.等比中项
等差数列:
定义
递推公式
通项公式
等差中项
前n项和Sn
2.4
出门见九堤,每堤有九木,每木有九巢,每巢有九鸟,每鸟有九雏,每雏有九毛,每毛有九色,问共有几堤,几木,几巢,几鸟,几雏,几毛,几色?(《孙子算经》)
堤、木,巢、鸟、雏、毛、色依次构成数列:
9,92,93,94,95,96, 97
“一尺之棰,日取其半,万世不竭”
——(《庄子》)
我们得到这样一组数:
已知某种细胞每分钟分裂一次,随着时间变化我们得到下面这组数:
1,2,4,8,16,32,……
(1)
9,92,93,94,95,96, 97
(3)
(2)
1, 2, 4, 8, 16, 32,……
有什么共同特征?
(1)
9,92,93,94,95,96, 97
(2)
(3)
1, 2, 4, 8, 16, 32,64
q=
q=
q=
等差数列:
如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,常用字母d表示(d∈R)。
等比数列:
如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,常用字母q表示(q≠0)。
判断数列{an}是等比数列的依据
下面的例子中哪些是等比数列?
① 3,6,12,24,48,……
② 0,0,0,0,0,0,……
③3,3,3,3,3,3,……
④2,-4,8,-16,32,……
是
不是
是
是
二、通项公式
……
1.递推法
二、通项公式
……
共计
n-1项
2.累乘法
【即时训练】
在等比数列{an}中,a1=2,q=3,求通项公式an。
【例1】在等比数列{an}中,
a2=18,a4=8,求a1和q.
【例2】一个等比数列的
第三项和第四项分别是12和18,
求它的第一项和第二项。
三、等比中项
如果a和b之间一个数G,
a、G和b成等比数列,那么G叫做a与b的等比中项,
这三个数满足关系式ab=G2
【例3】若三个正数a、b和c成等比数列,其中a= ,c= ,求b.
【例4】若a,2a+2,3a+3成等比数列,求实数a的值.
课堂小结:类比等差数列
1.等比数列定义
2.递推公式
3.通项公式
4.等比中项
