2020-2021学年青岛版七年级数学下册8.2角的比较-课件(22张PPT)
文档属性
| 名称 | 2020-2021学年青岛版七年级数学下册8.2角的比较-课件(22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 531.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 06:52:38 | ||
图片预览




文档简介
§8.2 角的比较
学习目标
1.掌握两种比较角的大小的方法:度量
法和叠合法.
2.会根据图形进行简单的角的和差计算.
3.掌握角的平行线的定义及数学表达式.
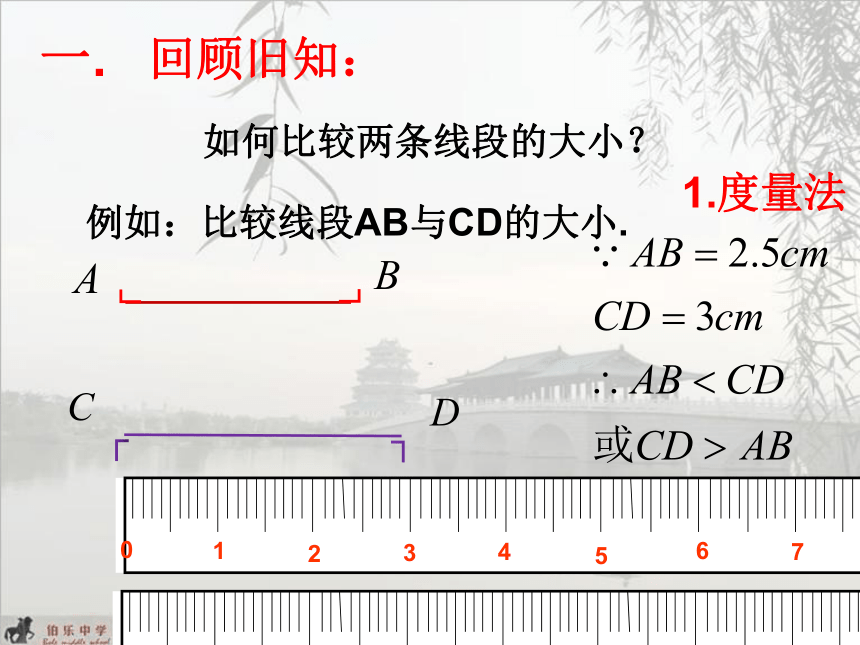
回顾旧知:
如何比较两条线段的大小?
例如:比较线段AB与CD的大小.
1
2
3
5
4
6
7
8
1
2
3
5
4
6
7
8
0
1
2
3
5
4
6
7
8
1
2
3
5
4
6
7
8
0
┐
┌
┌
┐
1.度量法
一.
┐
┌
┌
┐
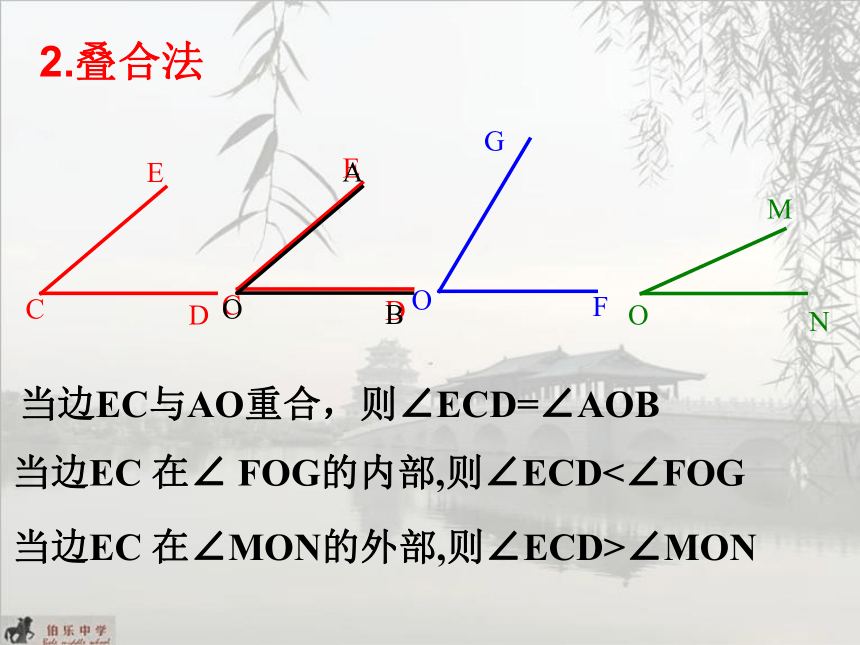
2.叠合法
二.思考一下:
A
O
B
1.度量法
角的大小与角的两边张开
的大小一致,与所画边的
长短无关.
2.叠合法
C
D
E
C
D
E
O
F
G
N
O
M
O
B
A
当边EC与AO重合,则∠ECD=∠AOB
当边EC 在∠ FOG的内部,则∠ECD<∠FOG
当边EC 在∠MON的外部,则∠ECD>∠MON
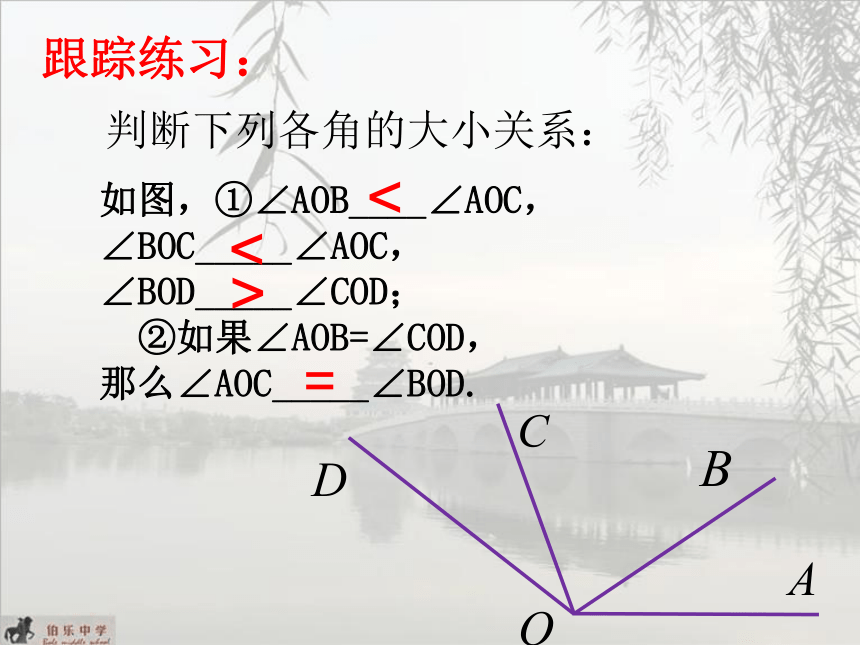
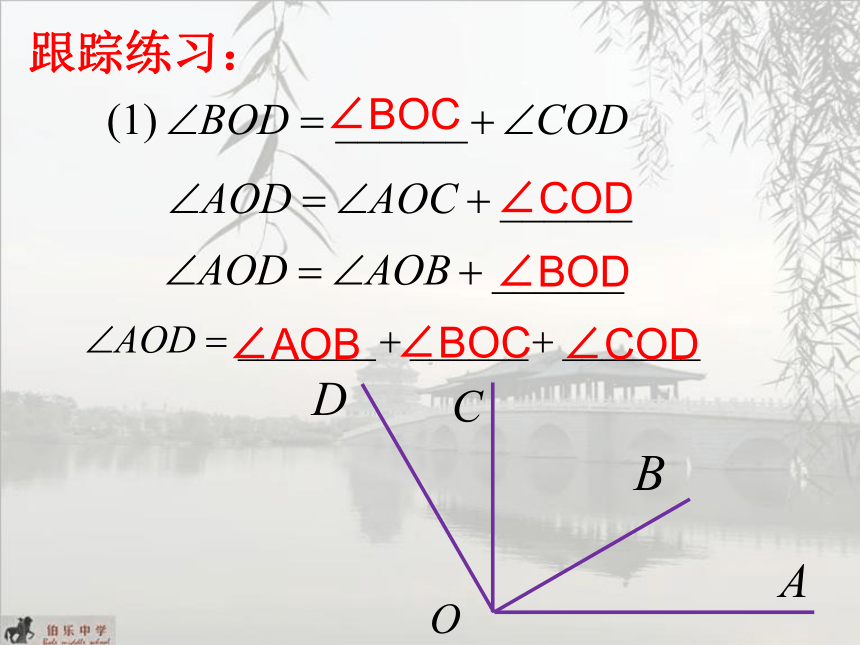
跟踪练习:
如图,①∠AOB____∠AOC,
∠BOC_____∠AOC,
∠BOD_____∠COD;
②如果∠AOB=∠COD,
那么∠AOC_____∠BOD.
判断下列各角的大小关系:
<
<
>
=
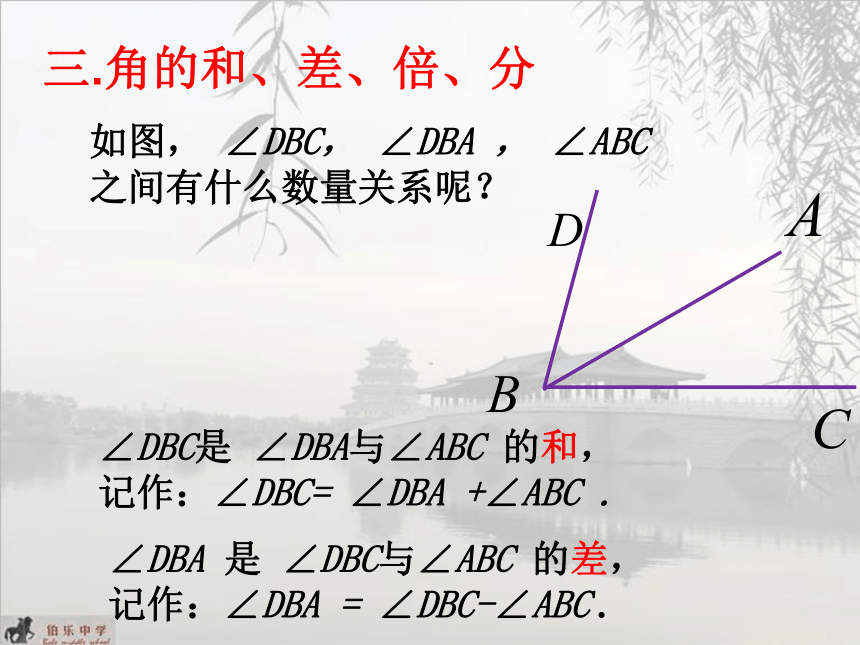
三.角的和、差、倍、分
如图, ∠DBC, ∠DBA , ∠ABC 之间有什么数量关系呢?
∠DBC是 ∠DBA与∠ABC 的和,
记作:∠DBC= ∠DBA +∠ABC .
∠DBA 是 ∠DBC与∠ABC 的差, 记作:∠DBA = ∠DBC-∠ABC .
跟踪练习:
∠BOC
∠COD
∠BOD
∠AOB
∠BOC
∠COD
∠BOD
∠AOB
∠BOC
︵
︵
︵
角的平分线:
A
B
O
C
一条射线把一个角分成了两个相等的角,
这条射线叫做角的平分线.
数学语言:
类似地:还有角的三等分线,如图
∠1=∠2=∠3
⌒
1
2
3
⌒
1
2
3
A
B
C
D
∴OB、OC是∠AOD的三等分线
︵
︵
同样,还可以作出角的四等分线、五等分线等。
跟踪练习:
射
FEM
DEM
DEF
DEF
FEM
DEM
2.如图OC、OD把∠AOB三等分,那么
∠COD=___∠AOB ∠AOD=___∠AOB
∠AOB=___∠AOD.
例1.
如图,在∠ AOC的内部画射线OB,在∠ AOC的外部画射线OD.∠ AOC 是哪两个角的和? 是哪两个角的差? ∠ BOD是哪两个角的和?是哪两个角的差?当∠ AOB= ∠ COD时,你能找出其它相等的角吗?
解:
由图可以看出:∠AOC是∠AOB与
∠BOC的和,又是∠AOD与∠COD
的差.即∠AOC=∠AOB+∠BOC,
∠AOC=∠AOD-∠COD.
同样地,∠BOD=∠BOC+∠COD,
∠BOD=∠AOD-∠AOB.
当∠AOB=∠COD时,∠AOC=∠BOD.
随堂练习
1.如果∠1-∠2=∠3,且∠4+∠2=∠1,那么∠3
和∠4的关系是( )
A.∠3>∠4 B.∠3=∠4
C.∠3<∠4 D.不确定
2.已知∠AOB=40°,过点O引射线OC若∠AOC∶
∠COB=2∶3,且OD平分∠AOB,则∠COD=____.
3.如图,∠1=15°,∠AOC=90°,点B,O,D在
同一条直线上,则∠2的度数为_____.
100°
B
)
)
105°
4.如图 ,小明将自己用的一副三角板摆成如图
形状,如果∠AOB=155°,那么∠COD=_____.
5.如图,OC平分∠AOD,∠BOD=2∠AOB,若
∠AOD=114°,则∠BOC的度数是______.
25°
19°
课堂小结:
如何比较角的大小?
有几种表示方法?
角的倍分关系怎样表示?
作业:
再见
学习目标
1.掌握两种比较角的大小的方法:度量
法和叠合法.
2.会根据图形进行简单的角的和差计算.
3.掌握角的平行线的定义及数学表达式.
回顾旧知:
如何比较两条线段的大小?
例如:比较线段AB与CD的大小.
1
2
3
5
4
6
7
8
1
2
3
5
4
6
7
8
0
1
2
3
5
4
6
7
8
1
2
3
5
4
6
7
8
0
┐
┌
┌
┐
1.度量法
一.
┐
┌
┌
┐
2.叠合法
二.思考一下:
A
O
B
1.度量法
角的大小与角的两边张开
的大小一致,与所画边的
长短无关.
2.叠合法
C
D
E
C
D
E
O
F
G
N
O
M
O
B
A
当边EC与AO重合,则∠ECD=∠AOB
当边EC 在∠ FOG的内部,则∠ECD<∠FOG
当边EC 在∠MON的外部,则∠ECD>∠MON
跟踪练习:
如图,①∠AOB____∠AOC,
∠BOC_____∠AOC,
∠BOD_____∠COD;
②如果∠AOB=∠COD,
那么∠AOC_____∠BOD.
判断下列各角的大小关系:
<
<
>
=
三.角的和、差、倍、分
如图, ∠DBC, ∠DBA , ∠ABC 之间有什么数量关系呢?
∠DBC是 ∠DBA与∠ABC 的和,
记作:∠DBC= ∠DBA +∠ABC .
∠DBA 是 ∠DBC与∠ABC 的差, 记作:∠DBA = ∠DBC-∠ABC .
跟踪练习:
∠BOC
∠COD
∠BOD
∠AOB
∠BOC
∠COD
∠BOD
∠AOB
∠BOC
︵
︵
︵
角的平分线:
A
B
O
C
一条射线把一个角分成了两个相等的角,
这条射线叫做角的平分线.
数学语言:
类似地:还有角的三等分线,如图
∠1=∠2=∠3
⌒
1
2
3
⌒
1
2
3
A
B
C
D
∴OB、OC是∠AOD的三等分线
︵
︵
同样,还可以作出角的四等分线、五等分线等。
跟踪练习:
射
FEM
DEM
DEF
DEF
FEM
DEM
2.如图OC、OD把∠AOB三等分,那么
∠COD=___∠AOB ∠AOD=___∠AOB
∠AOB=___∠AOD.
例1.
如图,在∠ AOC的内部画射线OB,在∠ AOC的外部画射线OD.∠ AOC 是哪两个角的和? 是哪两个角的差? ∠ BOD是哪两个角的和?是哪两个角的差?当∠ AOB= ∠ COD时,你能找出其它相等的角吗?
解:
由图可以看出:∠AOC是∠AOB与
∠BOC的和,又是∠AOD与∠COD
的差.即∠AOC=∠AOB+∠BOC,
∠AOC=∠AOD-∠COD.
同样地,∠BOD=∠BOC+∠COD,
∠BOD=∠AOD-∠AOB.
当∠AOB=∠COD时,∠AOC=∠BOD.
随堂练习
1.如果∠1-∠2=∠3,且∠4+∠2=∠1,那么∠3
和∠4的关系是( )
A.∠3>∠4 B.∠3=∠4
C.∠3<∠4 D.不确定
2.已知∠AOB=40°,过点O引射线OC若∠AOC∶
∠COB=2∶3,且OD平分∠AOB,则∠COD=____.
3.如图,∠1=15°,∠AOC=90°,点B,O,D在
同一条直线上,则∠2的度数为_____.
100°
B
)
)
105°
4.如图 ,小明将自己用的一副三角板摆成如图
形状,如果∠AOB=155°,那么∠COD=_____.
5.如图,OC平分∠AOD,∠BOD=2∠AOB,若
∠AOD=114°,则∠BOC的度数是______.
25°
19°
课堂小结:
如何比较角的大小?
有几种表示方法?
角的倍分关系怎样表示?
作业:
再见
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
