2020-2021学年青岛版七年级数学下册8.3角的度量(2)-课件(19张PPT)
文档属性
| 名称 | 2020-2021学年青岛版七年级数学下册8.3角的度量(2)-课件(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 405.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 06:54:25 | ||
图片预览





文档简介
§8.3 角的度量(2)
教学目标
1.认识一个角的余角和补角并掌握概念.
2.掌握余角和补角的性质.
)
)
1
2
α
β
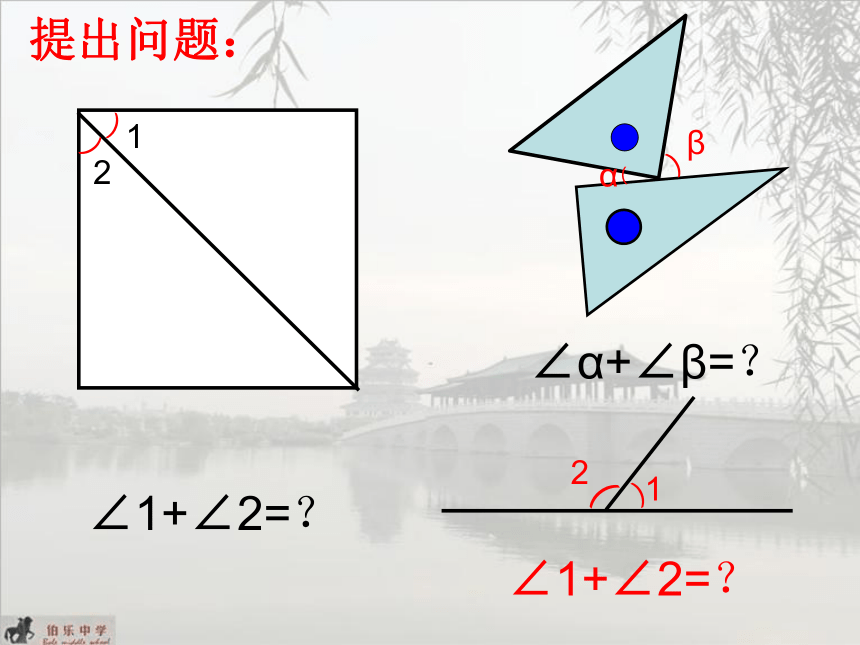
∠1+∠2=?
∠α+∠β=?
提出问题:
1
2
∠1+∠2=?
)
)
)
)
余角、
补角
1
2
3
4
如果两个角的和为90° (直角),那么称这两个角 互为余角 ,简称“互余”.
其中一个角叫做另一个角的余角.
如果两个角的和为180°(平角),那么称这两个角 互为补角,简称“互补”.
其中一个角叫做另一个角的补角.
∠1+∠2=90°
∠1+∠3=90°
∠3+∠4=180°
∠2+∠4=180°
对定义的正确理解:
(1)定义中的“互为”一词如何理解?
如果?1与?2互余,那么?1的余角是?2 ,同样?2的余角是?1 ;如果?1与?2互补,那么?1的补角是?2 , 同样?2的补角是?1。
┐
1
2
1
2
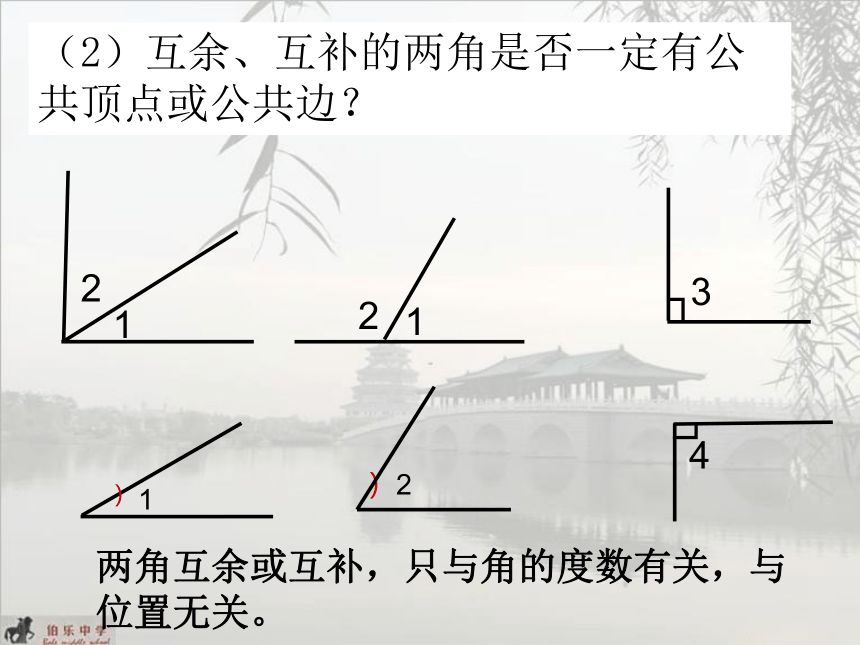
(2)互余、互补的两角是否一定有公共顶点或公共边?
1
2
1
2
)
1
)
2
┐
3
┐
4
两角互余或互补,只与角的度数有关,与位置无关。
(3)∠1 + ∠2 + ∠3 = 90°(180°),能说∠1 、∠2、 ∠3 互余(互补)吗?
不能,互余或互补是两个角之间的数量关系。
1
2
3
1
2
3
问题:
1.钝角有余角吗?
2.直角有补角吗?
3.若一个角为∠α那么它的余角如何表示?
补角呢?
随堂练习
1.在图中找出互余和互补的角
┐
┌
2.一个角的度数为20°,那么它的余角
为____.补角为____.
3.一个角的余角为35°,那么这个角为______.
4.
的补角是 .
)
(
5.判断
(1).90度的角叫余角。 ( )
(2).若
,则
互余.
(3).互余的两个角一定都是锐角,两个锐角
一定互余. ( )
例3 一个角的补角是它的余角的3倍,
求这个角的度数.
解:设这个角是 ,那么它的补角是(180- )
余角是( 90- )根据题意,得
180- =3( 90- )
解这个方程,得
=45
所以,这个角45o
交流与发现
B
O
C
A
D
)
1
)
2
)
3
1.如图,∠AOC=
∠BOD=90°找出
∠3的两个余角,
它们有什么关系?
为什么?
∴同角的余角相等.
几何语言:
∵ ∠1+ ∠ 3= 900
∠ 2+∠ 3 = 900
∴ ∠ 1 = ∠ 2
(同角的余角相等)
2.如图,∠1和∠2互余,∠3和∠4互余,若
∠1=∠3,那么∠2和∠4相等吗?为什么?
理由:∵∠1与∠2互余
∴∠2=90o-∠1
∵∠3与∠4互余
∴∠4=90o-∠3
又∵∠1=∠3
∴∠2=∠4
解: ∠2与∠4相等
)
)
)
1
2
)
3
4
∴等角的余角相等.
余角的性质:
同角或等角的余角相等.
几何语言:
∵ ∠1+ ∠ 2= 900
∠ 3+ ∠ 4 = 900
又∵ ∠ 1 = ∠ 3
∴ ∠ 2 = ∠ 4
(等角的余角相等)
)
1
2
)
3
4
3.如图,∠1=∠2,∠3,∠4分别是∠1,∠2的
补角时,∠3=∠4吗?为什么?
)
)
)
)
1
2
3
4
补角的性质:
同角或等角的补角相等.
跟踪练习
如图1,若∠1与∠2互余,∠2与∠3互余,则
∠___=∠___,根据是_____.
如图2,若∠1与∠2互补,∠2与∠3互补,则
∠___=∠___.根据是_____.
)
)
)
)
)
)
1
2
3
3
1
2
图1
图2
1.
2.
课堂小结
师生共同总结本节内容.
作业
五.归纳总结,拓展思维
.作业
教学目标
1.认识一个角的余角和补角并掌握概念.
2.掌握余角和补角的性质.
)
)
1
2
α
β
∠1+∠2=?
∠α+∠β=?
提出问题:
1
2
∠1+∠2=?
)
)
)
)
余角、
补角
1
2
3
4
如果两个角的和为90° (直角),那么称这两个角 互为余角 ,简称“互余”.
其中一个角叫做另一个角的余角.
如果两个角的和为180°(平角),那么称这两个角 互为补角,简称“互补”.
其中一个角叫做另一个角的补角.
∠1+∠2=90°
∠1+∠3=90°
∠3+∠4=180°
∠2+∠4=180°
对定义的正确理解:
(1)定义中的“互为”一词如何理解?
如果?1与?2互余,那么?1的余角是?2 ,同样?2的余角是?1 ;如果?1与?2互补,那么?1的补角是?2 , 同样?2的补角是?1。
┐
1
2
1
2
(2)互余、互补的两角是否一定有公共顶点或公共边?
1
2
1
2
)
1
)
2
┐
3
┐
4
两角互余或互补,只与角的度数有关,与位置无关。
(3)∠1 + ∠2 + ∠3 = 90°(180°),能说∠1 、∠2、 ∠3 互余(互补)吗?
不能,互余或互补是两个角之间的数量关系。
1
2
3
1
2
3
问题:
1.钝角有余角吗?
2.直角有补角吗?
3.若一个角为∠α那么它的余角如何表示?
补角呢?
随堂练习
1.在图中找出互余和互补的角
┐
┌
2.一个角的度数为20°,那么它的余角
为____.补角为____.
3.一个角的余角为35°,那么这个角为______.
4.
的补角是 .
)
(
5.判断
(1).90度的角叫余角。 ( )
(2).若
,则
互余.
(3).互余的两个角一定都是锐角,两个锐角
一定互余. ( )
例3 一个角的补角是它的余角的3倍,
求这个角的度数.
解:设这个角是 ,那么它的补角是(180- )
余角是( 90- )根据题意,得
180- =3( 90- )
解这个方程,得
=45
所以,这个角45o
交流与发现
B
O
C
A
D
)
1
)
2
)
3
1.如图,∠AOC=
∠BOD=90°找出
∠3的两个余角,
它们有什么关系?
为什么?
∴同角的余角相等.
几何语言:
∵ ∠1+ ∠ 3= 900
∠ 2+∠ 3 = 900
∴ ∠ 1 = ∠ 2
(同角的余角相等)
2.如图,∠1和∠2互余,∠3和∠4互余,若
∠1=∠3,那么∠2和∠4相等吗?为什么?
理由:∵∠1与∠2互余
∴∠2=90o-∠1
∵∠3与∠4互余
∴∠4=90o-∠3
又∵∠1=∠3
∴∠2=∠4
解: ∠2与∠4相等
)
)
)
1
2
)
3
4
∴等角的余角相等.
余角的性质:
同角或等角的余角相等.
几何语言:
∵ ∠1+ ∠ 2= 900
∠ 3+ ∠ 4 = 900
又∵ ∠ 1 = ∠ 3
∴ ∠ 2 = ∠ 4
(等角的余角相等)
)
1
2
)
3
4
3.如图,∠1=∠2,∠3,∠4分别是∠1,∠2的
补角时,∠3=∠4吗?为什么?
)
)
)
)
1
2
3
4
补角的性质:
同角或等角的补角相等.
跟踪练习
如图1,若∠1与∠2互余,∠2与∠3互余,则
∠___=∠___,根据是_____.
如图2,若∠1与∠2互补,∠2与∠3互补,则
∠___=∠___.根据是_____.
)
)
)
)
)
)
1
2
3
3
1
2
图1
图2
1.
2.
课堂小结
师生共同总结本节内容.
作业
五.归纳总结,拓展思维
.作业
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
