2020-2021学年青岛版七年级数学下册8.4对顶角课件(共17张PPT)
文档属性
| 名称 | 2020-2021学年青岛版七年级数学下册8.4对顶角课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 471.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 00:00:00 | ||
图片预览




文档简介
§8.4 对顶角
1、理解对顶角的概念,能在图形中辨认对顶角;
2、掌握对顶角相等的性质和它的推理过程;
3、会用对顶角的性质进行有关的推理和计算.
学习目标
知识回顾
1.若∠1+∠2=90°,那么∠1与∠2_____.
2.若∠1+∠2=180°,那么∠1与∠2____.
3.余角和补角的性质是什么?
)
)
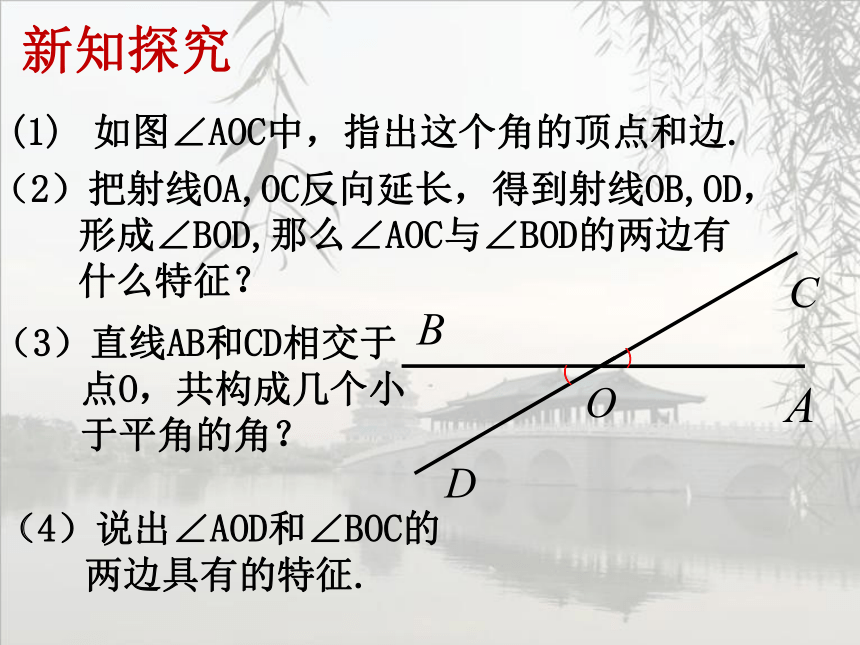
(1) 如图∠AOC中,指出这个角的顶点和边.
(2)把射线OA,OC反向延长,得到射线OB,OD,
形成∠BOD,那么∠AOC与∠BOD的两边有
什么特征?
(3)直线AB和CD相交于
点O,共构成几个小
于平角的角?
(4)说出∠AOD和∠BOC的
两边具有的特征.
新知探究
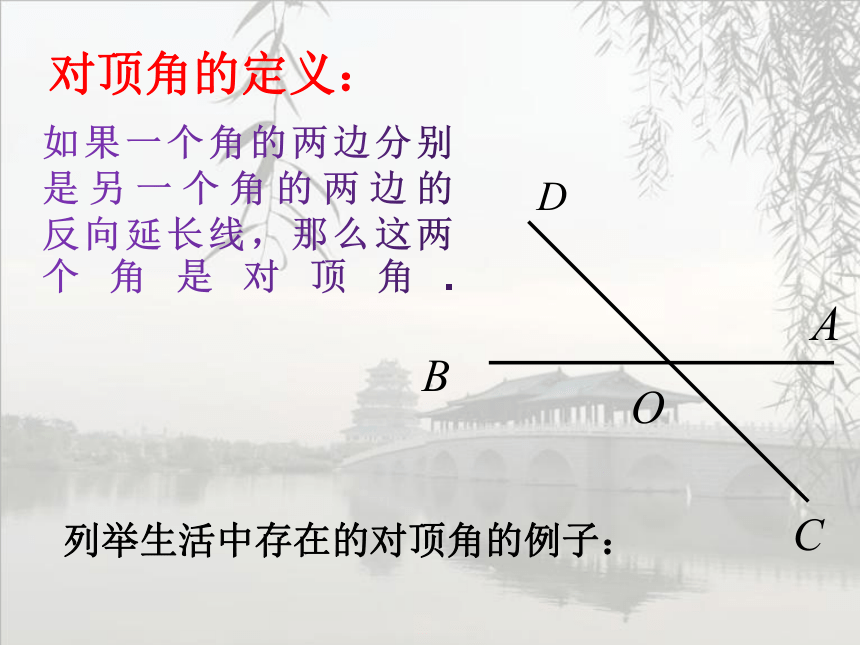
对顶角的定义:
如果一个角的两边分别是另一个角的两边的
反向延长线,那么这两
个角是对顶角.
列举生活中存在的对顶角的例子:
满足对顶角的三个条件:
(1)是两条直线相交而成的;
(2)有一个公共点;
(3)没有公共边.
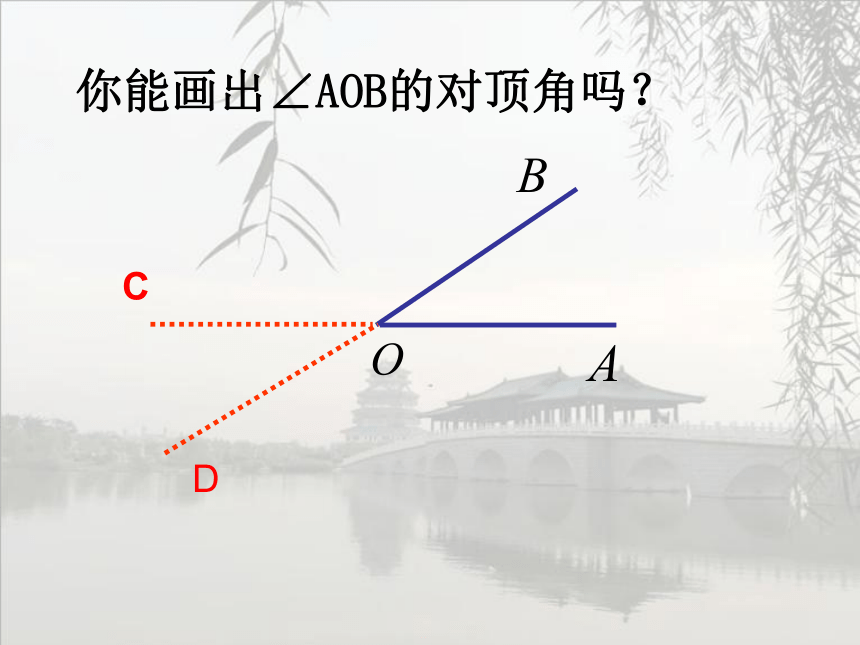
你能画出∠AOB的对顶角吗?
D
C
练一练:下列各图中,∠l和∠2是
对顶角吗?为什么?
√
×
×
×
×
×
如图,两条直线相交形成了∠1、∠2、∠3、∠4,
那么对顶角∠1与∠3相等吗? ∠2与∠4呢?
想一想:
)
)
)
)
1
2
3
4
解:∠1=∠3,∠2=∠4.
理由:∵∠1+∠2=180°,
∠2+∠3=180°,
∴∠1=∠3(同角的补角相等).
同理:∠2=∠4.
对顶角的性质:
如果两个角是对顶角,那么这 两个角相等.
简称:对顶角相等.
下列说法中,正确的有( )
①对顶角相等
②相等的角是对顶角
③不是对顶角的两个角就不相等
④不相等的角不是对顶角
A.1个 B.2个 C.3个 D.0个
1.
要测量两堵墙所成的角的度数,但人不能进入围墙,如何测量?
2.
)
如图,直线AB和CD相交于点O,射线OE是∠BOD的角平分线,已知∠AOD=110°,分别求∠COB,∠AOC,∠BOE,∠EOD的度数。
例1.
解:
∵∠COB与∠AOD是对顶角,
∴∠COB=∠AOD=110°.
∠AOC=∠COD-∠AOD
=180°-110°=70°
又∵∠BOD与∠AOC是对顶角,
∴∠BOD=∠AOC=70°.
由OE平分∠BOD,得∠BOE=∠EOD=
1.如图,两条直线相交所形成的四个角中,已知 ∠1=30°,那么∠2、∠3和∠4各等于多少度?
2.如图,直线AB,CD交于点O,
射线OM平分∠AOC,若∠BOD=76°,
则∠BOM=( ).
随堂练习
)
)
)
)
∠2=150°,∠3=30°,∠4=150°.
142°
3.如图,直线AB、EF相交于点D,∠ADC=900。
(1)∠1的对顶角是_______;∠2的余
角有___________。
(2)若∠1与∠2的度数之比为1︰4,
求∠BDF的度数。
)
)
请同学们谈谈本节课的收获与体会
课堂小结
作业
1、理解对顶角的概念,能在图形中辨认对顶角;
2、掌握对顶角相等的性质和它的推理过程;
3、会用对顶角的性质进行有关的推理和计算.
学习目标
知识回顾
1.若∠1+∠2=90°,那么∠1与∠2_____.
2.若∠1+∠2=180°,那么∠1与∠2____.
3.余角和补角的性质是什么?
)
)
(1) 如图∠AOC中,指出这个角的顶点和边.
(2)把射线OA,OC反向延长,得到射线OB,OD,
形成∠BOD,那么∠AOC与∠BOD的两边有
什么特征?
(3)直线AB和CD相交于
点O,共构成几个小
于平角的角?
(4)说出∠AOD和∠BOC的
两边具有的特征.
新知探究
对顶角的定义:
如果一个角的两边分别是另一个角的两边的
反向延长线,那么这两
个角是对顶角.
列举生活中存在的对顶角的例子:
满足对顶角的三个条件:
(1)是两条直线相交而成的;
(2)有一个公共点;
(3)没有公共边.
你能画出∠AOB的对顶角吗?
D
C
练一练:下列各图中,∠l和∠2是
对顶角吗?为什么?
√
×
×
×
×
×
如图,两条直线相交形成了∠1、∠2、∠3、∠4,
那么对顶角∠1与∠3相等吗? ∠2与∠4呢?
想一想:
)
)
)
)
1
2
3
4
解:∠1=∠3,∠2=∠4.
理由:∵∠1+∠2=180°,
∠2+∠3=180°,
∴∠1=∠3(同角的补角相等).
同理:∠2=∠4.
对顶角的性质:
如果两个角是对顶角,那么这 两个角相等.
简称:对顶角相等.
下列说法中,正确的有( )
①对顶角相等
②相等的角是对顶角
③不是对顶角的两个角就不相等
④不相等的角不是对顶角
A.1个 B.2个 C.3个 D.0个
1.
要测量两堵墙所成的角的度数,但人不能进入围墙,如何测量?
2.
)
如图,直线AB和CD相交于点O,射线OE是∠BOD的角平分线,已知∠AOD=110°,分别求∠COB,∠AOC,∠BOE,∠EOD的度数。
例1.
解:
∵∠COB与∠AOD是对顶角,
∴∠COB=∠AOD=110°.
∠AOC=∠COD-∠AOD
=180°-110°=70°
又∵∠BOD与∠AOC是对顶角,
∴∠BOD=∠AOC=70°.
由OE平分∠BOD,得∠BOE=∠EOD=
1.如图,两条直线相交所形成的四个角中,已知 ∠1=30°,那么∠2、∠3和∠4各等于多少度?
2.如图,直线AB,CD交于点O,
射线OM平分∠AOC,若∠BOD=76°,
则∠BOM=( ).
随堂练习
)
)
)
)
∠2=150°,∠3=30°,∠4=150°.
142°
3.如图,直线AB、EF相交于点D,∠ADC=900。
(1)∠1的对顶角是_______;∠2的余
角有___________。
(2)若∠1与∠2的度数之比为1︰4,
求∠BDF的度数。
)
)
请同学们谈谈本节课的收获与体会
课堂小结
作业
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
