2020-2021学年青岛版七年级数学下册9.3平行线的性质课件(共18张PPT)
文档属性
| 名称 | 2020-2021学年青岛版七年级数学下册9.3平行线的性质课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 10:06:35 | ||
图片预览




文档简介
§9.3平行线的性质
学习目标
1.掌握平行线的三条性质,应用平行线
的性质进行简单的推理和计算.
2.理解两条平行线之间的距离,会度量
这一距离.
一.课堂引入
已知直线AB及直线外一点P,用直尺和三角尺
作出过点P与AB平行的直线CD.
E
F
)
)
)
)
)
)
)
)
1
2
3
4
5
6
7
8
(2)画一条截线EF截
直线AB,CD构成8个角.
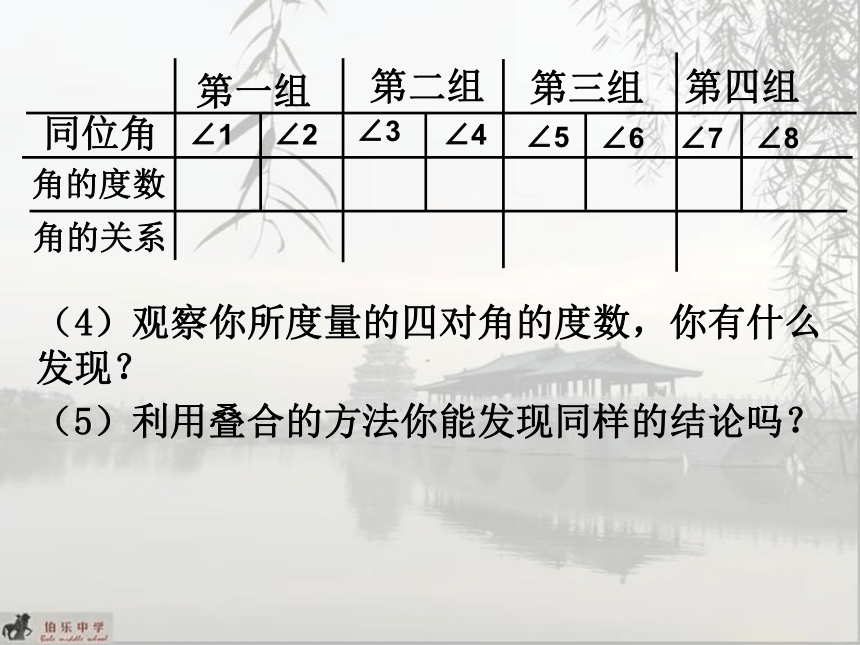
(3)指出图中的同位角
并度量这些角的度数,
填在下表中:
∠1和∠7,∠2和∠8
∠4和∠6,∠3和∠5.
(1)回顾画平行线的方法.
同位角
角的度数
角的关系
第一组
第二组
第三组
第四组
(4)观察你所度量的四对角的度数,你有什么
发现?
(5)利用叠合的方法你能发现同样的结论吗?
∠1
∠2
∠3
∠4
∠5
∠6
∠7
∠8
二.课堂探究
1.
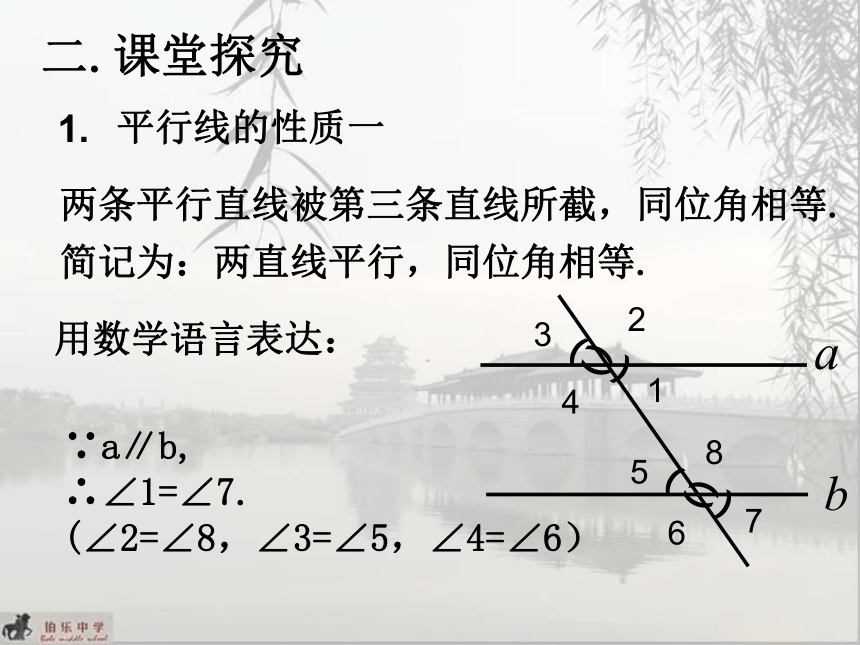
平行线的性质一
两条平行直线被第三条直线所截,同位角相等.
简记为:两直线平行,同位角相等.
用数学语言表达:
)
)
)
)
)
)
)
)
1
2
3
4
5
6
7
8
∵a∥b,
∴∠1=∠7.
(∠2=∠8,∠3=∠5,∠4=∠6)
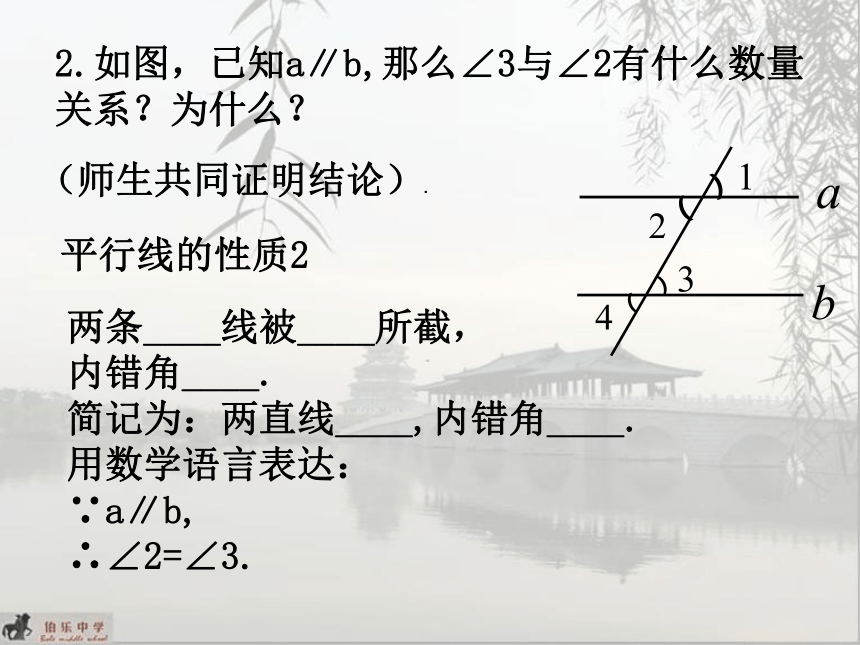
2.如图,已知a∥b,那么∠3与∠2有什么数量
关系?为什么?
)
)
)
)
(师生共同证明结论).
平行线的性质2
两条____线被____所截,
内错角____.
简记为:两直线____,内错角____.
用数学语言表达:
∵a∥b,
∴∠2=∠3.
3.如图,已知a∥b,那么∠3与∠2有什么数量
关系?为什么?
)
)
)
(师生共同证明结论)
平行线的性质三
两条___线被___所截,
同旁内角_____.
简记为:两直线____,同旁内角____.
用数学语言表达:
∵a∥b,
∴∠2+∠3=180°.
随堂练习
1.如图,已知AB∥CD,∠1=110°,求∠C的度数.
解:∵∠1=110°(已知),
∴∠1=∠___( ).
又∵AB∥CD(已知),
∴∠___=___( ).
∴∠C=___°.
)
)
)
)
2.如图,AB∥CD,∠3=∠4,则下列结论中不
成立的是____.
)
)
)
)
)
A.∠1=∠4
B.∠3=∠5
C.∠1=∠5
D.∠2+∠4=180°
三.应用举例
已知:如图,直线a∥b,c∥d,∠1=106°.
求∠2,∠3的度数.
)
)
)
解:∵a∥b(已知),
∴∠1=____( ).
又∵∠1=110°( ),
∴∠2=____.
∵c∥d(已知)
∴∠2=____( ).
∴∠3=____.
四.交流与发现
┐
┐
如图,
(1)画两条平行线 和 .
(2)在直线 上任取一点A,经过点A画AC⊥
垂足为C,那么AC与直线 有什么位置关系?为什么?
(3)在直线上再任取一点B,经过点B画BD⊥
垂足为D,AC与BD有什么位置关系?为什么?
┐
┐
(4)用刻度尺或圆规比较
垂线段AC与垂线段BD的
大小,你发现了什么?
与同学交流.
平行线之间的距离:
如果两条直线平行,那么 其中一条直线上每个
点的哦另一条直线的距都相等.
(5)怎样度量两平行线之间的距离?
五.课堂小结
1.知识的梳理.
(由学生总结)
2.疑惑点排查.
(学生提出问题,教师或学生当堂解决).
六.作业
课堂检测
1.两条平行线被第三条直线所截,_____相等,
____相等,_____相等.
2.学写证明过程.
证明:∵AB∥CD(已知),
∴∠1=∠3( ).
又∵∠3=∠2( ),
∴∠1=∠2(等量代换).
又∵∠4+∠2=180°( ),
∴∠1+∠4=180°(等量代换).
)
)
)
)
3.如图,直线a∥b,点B在直线b上,且AB⊥BC,
∠1=55°,则∠2=____.
4.如图,AB∥DE,BC∥EF,
求∠B+∠E的度数.
┐
)
)
(第3题图)
(第4题图)
5.如图,平行四边形ABCD中,AB∥CD,AD∥BC.
(1)图中相等的角有_______,
互补的角有________.
(2)连接AC,则图中相等的角还有_______.
再见
学习目标
1.掌握平行线的三条性质,应用平行线
的性质进行简单的推理和计算.
2.理解两条平行线之间的距离,会度量
这一距离.
一.课堂引入
已知直线AB及直线外一点P,用直尺和三角尺
作出过点P与AB平行的直线CD.
E
F
)
)
)
)
)
)
)
)
1
2
3
4
5
6
7
8
(2)画一条截线EF截
直线AB,CD构成8个角.
(3)指出图中的同位角
并度量这些角的度数,
填在下表中:
∠1和∠7,∠2和∠8
∠4和∠6,∠3和∠5.
(1)回顾画平行线的方法.
同位角
角的度数
角的关系
第一组
第二组
第三组
第四组
(4)观察你所度量的四对角的度数,你有什么
发现?
(5)利用叠合的方法你能发现同样的结论吗?
∠1
∠2
∠3
∠4
∠5
∠6
∠7
∠8
二.课堂探究
1.
平行线的性质一
两条平行直线被第三条直线所截,同位角相等.
简记为:两直线平行,同位角相等.
用数学语言表达:
)
)
)
)
)
)
)
)
1
2
3
4
5
6
7
8
∵a∥b,
∴∠1=∠7.
(∠2=∠8,∠3=∠5,∠4=∠6)
2.如图,已知a∥b,那么∠3与∠2有什么数量
关系?为什么?
)
)
)
)
(师生共同证明结论).
平行线的性质2
两条____线被____所截,
内错角____.
简记为:两直线____,内错角____.
用数学语言表达:
∵a∥b,
∴∠2=∠3.
3.如图,已知a∥b,那么∠3与∠2有什么数量
关系?为什么?
)
)
)
(师生共同证明结论)
平行线的性质三
两条___线被___所截,
同旁内角_____.
简记为:两直线____,同旁内角____.
用数学语言表达:
∵a∥b,
∴∠2+∠3=180°.
随堂练习
1.如图,已知AB∥CD,∠1=110°,求∠C的度数.
解:∵∠1=110°(已知),
∴∠1=∠___( ).
又∵AB∥CD(已知),
∴∠___=___( ).
∴∠C=___°.
)
)
)
)
2.如图,AB∥CD,∠3=∠4,则下列结论中不
成立的是____.
)
)
)
)
)
A.∠1=∠4
B.∠3=∠5
C.∠1=∠5
D.∠2+∠4=180°
三.应用举例
已知:如图,直线a∥b,c∥d,∠1=106°.
求∠2,∠3的度数.
)
)
)
解:∵a∥b(已知),
∴∠1=____( ).
又∵∠1=110°( ),
∴∠2=____.
∵c∥d(已知)
∴∠2=____( ).
∴∠3=____.
四.交流与发现
┐
┐
如图,
(1)画两条平行线 和 .
(2)在直线 上任取一点A,经过点A画AC⊥
垂足为C,那么AC与直线 有什么位置关系?为什么?
(3)在直线上再任取一点B,经过点B画BD⊥
垂足为D,AC与BD有什么位置关系?为什么?
┐
┐
(4)用刻度尺或圆规比较
垂线段AC与垂线段BD的
大小,你发现了什么?
与同学交流.
平行线之间的距离:
如果两条直线平行,那么 其中一条直线上每个
点的哦另一条直线的距都相等.
(5)怎样度量两平行线之间的距离?
五.课堂小结
1.知识的梳理.
(由学生总结)
2.疑惑点排查.
(学生提出问题,教师或学生当堂解决).
六.作业
课堂检测
1.两条平行线被第三条直线所截,_____相等,
____相等,_____相等.
2.学写证明过程.
证明:∵AB∥CD(已知),
∴∠1=∠3( ).
又∵∠3=∠2( ),
∴∠1=∠2(等量代换).
又∵∠4+∠2=180°( ),
∴∠1+∠4=180°(等量代换).
)
)
)
)
3.如图,直线a∥b,点B在直线b上,且AB⊥BC,
∠1=55°,则∠2=____.
4.如图,AB∥DE,BC∥EF,
求∠B+∠E的度数.
┐
)
)
(第3题图)
(第4题图)
5.如图,平行四边形ABCD中,AB∥CD,AD∥BC.
(1)图中相等的角有_______,
互补的角有________.
(2)连接AC,则图中相等的角还有_______.
再见
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
