小题压轴题专练41—抛物线(3)-2021届高三数学二轮复习 Word版含解析
文档属性
| 名称 | 小题压轴题专练41—抛物线(3)-2021届高三数学二轮复习 Word版含解析 |  | |
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 08:39:14 | ||
图片预览




文档简介
小题压轴题专练41—抛物线(3)
单选题
1.已知抛物线与轴交于,两点,点的坐标为,圆过,,三点,当实数变化时,存在一条定直线被圆截得的弦长为定值,则此定直线方程为
A. B. C. D.
解:与轴交于,,
设两点,,,,
设圆的方程为,取,可得.
则方程与方程等价,则,,
则圆的方程为.
圆过,,即,
得圆的方程为,
即,
由圆系方程可知,圆经过圆与直线的交点,
则圆被直线所截弦长为定值.
故选:.
2.已知抛物线的焦点为,准线为,是上一点,是直线与抛物线的一个交点,若,则
A.3 B.4或 C. D.或
解:当在的延长线时,过向准线作垂线,垂足为,根据已知条件,,
结合抛物线的定义得,
,,
.
当在之间时,过向准线作垂线,垂足为,根据已知条件,,
结合抛物线的定义得,
,,
故选:.
3.已知抛物线的焦点为,过点作倾斜角为的直线交抛物线于,两点,点,在抛物线准线上的射影分别是,,若四边形的面积为,则该抛物线的方程为
A. B. C. D.
解:,抛物线的焦点为,,准线方程为:,
直线的倾斜角为,斜率,
直线的方程为,代入,
得:,则,,
令,,,,,
则,
四边形是直角梯形,
,
,
抛物线的方程为,
故选:.
4.已知抛物线的焦点为,过的直线交于,两点,点在第一象限,,为坐标原点,则四边形面积最小时直线的方程是
A. B. C. D.
解:抛物线的焦点,设直线的方程为,
联立,可得.
设,,,,,则,
四边形的面积.
令,则,
当时,,单调递减,当时,,单调递增,
当时,即当时,四边形的面积最小,此时,,,
直线的方程为.
故选:.
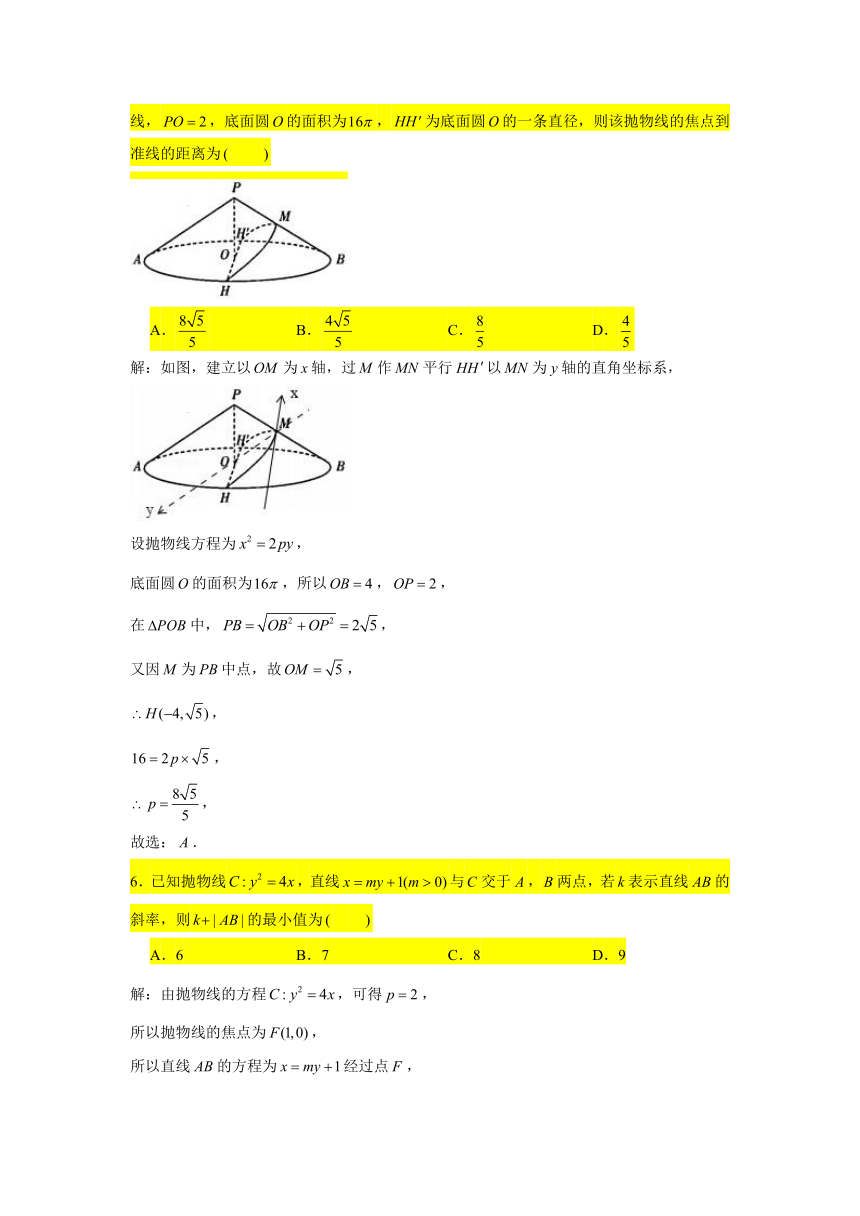
5.在《西游记》中,凤仙郡太守生气时误推倒祭祀玉帝的贡桌,玉帝一怒之下下令凤仙郡三年不能下雨,于是孙悟空和猪八戒上天庭去找玉帝理论,玉帝要求鸡要吃完米,狗要舔完面,火烧断了锁才能下雨.孙悟空打量着形如圆锥的面山,让猪八戒从面山脚下出发经过的中点到,大致观察一下该面山,如图所示,若猪八戒经过的路线为一条抛物线,,底面圆的面积为,为底面圆的一条直径,则该抛物线的焦点到准线的距离为
A. B. C. D.
解:如图,建立以为轴,过作平行以为轴的直角坐标系,
设抛物线方程为,
底面圆的面积为,所以,,
在中,,
又因为中点,故,
,
,
,
故选:.
6.已知抛物线,直线与交于,两点,若表示直线的斜率,则的最小值为
A.6 B.7 C.8 D.9
解:由抛物线的方程,可得,
所以抛物线的焦点为,
所以直线的方程为经过点,
设,,,,
由,得,
△成立,
所以,
所以,
所以,
因为直线的斜率,
所以,
令,,
则,
当时,,单调递减,
当时,,单调递增,
所以.
所以的最小值为7,
故选:.
7.已知抛物线的焦点为,直线与交于,两点,且,线段的垂直平分线与轴的交点为,则
A. B.2 C. D.
解:设,,,,联立直线与抛物线方程,
,
,
则的垂直平分线为,
则点,
则,
.
故选:.
8.已知抛物线的焦点为,过点斜率为的直线交该抛物线于,在第一象限),直线与圆交于点,在第一象限),为坐标原点,则与的面积之比为
A. B. C. D.
解:由抛物线的方程可得,
则可得直线的方程为:,与抛物线方程联立可得:
,解得,
因为点在第一象限,所以,
所以,,
又由圆的方程可得圆心为,半径,
所以,,
因为三角形的面积为,,
又,四点共线,所以,
所以,
故选:.
多选题
9.已知抛物线的准线方程为,焦点为,为坐标原点,,,,是上两点,则下列说法正确的是
A.点的坐标为
B.若,则的中点到轴距离的最小值为8
C.若直线过点,则以为直径的圆过点
D.若直线与的斜率之积为,则直线过点
解:抛物线的准线方程为,
的解析式为:,
对于:准线方程为,故焦点,故正确;
对于:设,则,
整理得:,故,,故中点为,
,
,,
当且仅当时“”成立,故错误;
对于:设,则,则,
的中点到的距离,
故以为直径的圆不过点,故错误;
对于,
,故,即,过,故正确.
故选:.
10.已知抛物线的准线为,焦点为,原点为,过的直线交抛物线于点、,在第一象限,分别过、作准线的垂线于、,直线的倾斜角为.则下列说法正确的是
A. B.
C.、、三点共线 D.以为直径的圆与轴相切
解:设,,,,
由题意知,直线的方程为,且,
将其与联立,消去得,,
①,②,
,
,即③,
由②③解得,,,
代入①得,,解得,
,,即选项正确;
把,分别代入中,可得,,,,
,
,
由选项可知,,,
,即选项错误;
准线于,,,
,,
、、三点共线,即选项正确;
,,,,
,线段的中点坐标为,
线段的中点横坐标恰为的一半,
以为直径的圆与轴相切,即选项正确.
故选:.
11.已知抛物线的焦点为,准线交轴于点,直线过且交于不同的,两点,在线段上,点为在上的射影,下列命题正确的是
A.若,则
B.若,,三点共线,则
C.若,则
D.对于任意直线,都有
解:如图示:
由题意的焦点为,准线,,
不妨设,联立,则,
即,则,,
设,,,,,
对于,则,,,
整理得:,则,
假设,则直线的斜率为1,
即时,解方程,得,,
故,故错误;
对于:点为在上的射影,则,
,,三点共线时,有,
解得:,,故,,
故,故正确;
对于:作于,由,得,
故,故正确;
对于:由,
而,由,得△,解得:,
故,故正确;
故选:.
12.已知抛物线,过其准线上的点作的两条切线,切点分别为、,下列说法正确的是
A. B.
C.直线的斜率为 D.线段中点的横坐标为1
解:由准线上的点的坐标可得准线方程为,即,
解得,所以不正确;
所以抛物线的方程为;
显然过点的切线的斜率存在且不为0,
设过的切线方程为,
联立,整理可得,
则△,
可得,所以,所以与垂直,所以正确;
设,,,,则,
抛物线的方程,即,所以,
切线的方程为,
即,将点代入可得,
同理切线的方程为,
所以直线的方程为,所以直线的斜率为,所以正确;
中,因为直线的斜率为,
所以,即线段的中点的横坐标为1,所以正确,
故选:.
填空题
13.已知为抛物线的焦点,,点在抛物线上且满足.若这样的点有且只有一个,则实数的值为 .
解:设,,由抛物线的性质,可得,
,,
由,得,把代入,
可得:.
点有且只有一个,方程有两相等实数根.
则△,
整理得,解得.
故答案为:.
14.已知为抛物线的焦点,过作斜率为的直线和抛物线交于,两点,延长,交抛物线于,两点,直线的斜率为.若,则 .
解:设过点作斜率为的直线方程为:,
联立方程,消去可得:,
设,,,,
,
设,,,,
则,同理,
设所在的直线方程为,
联立方程,消去得:,
,同理可得,
则.
15.已知圆,抛物线,抛物线焦点是,过点的直线与抛物线交于点、,与圆交于点、,点、在第一象限,则的最小值是 .
解:由抛物线方程可得,,
当直线的斜率存在时,设的方程为,
代入,整理得,.
设,,,,
,又圆的半径等于1,
,,
因此,
当且仅当,即时等号成立.
当直线的斜率不存在时,可求得.
综上,的最小值为22.
故答案为:22.
16.已知点,为抛物线的焦点,过点且斜率为的直线与抛物线交于,两点,若,则的取值范围是 .
解:由题意知,,设,,,,
直线的方程为,
由,得.
,,
由,得
,
即,解得,
又,,即.
的取值范围是,.
故答案为:,.
单选题
1.已知抛物线与轴交于,两点,点的坐标为,圆过,,三点,当实数变化时,存在一条定直线被圆截得的弦长为定值,则此定直线方程为
A. B. C. D.
解:与轴交于,,
设两点,,,,
设圆的方程为,取,可得.
则方程与方程等价,则,,
则圆的方程为.
圆过,,即,
得圆的方程为,
即,
由圆系方程可知,圆经过圆与直线的交点,
则圆被直线所截弦长为定值.
故选:.
2.已知抛物线的焦点为,准线为,是上一点,是直线与抛物线的一个交点,若,则
A.3 B.4或 C. D.或
解:当在的延长线时,过向准线作垂线,垂足为,根据已知条件,,
结合抛物线的定义得,
,,
.
当在之间时,过向准线作垂线,垂足为,根据已知条件,,
结合抛物线的定义得,
,,
故选:.
3.已知抛物线的焦点为,过点作倾斜角为的直线交抛物线于,两点,点,在抛物线准线上的射影分别是,,若四边形的面积为,则该抛物线的方程为
A. B. C. D.
解:,抛物线的焦点为,,准线方程为:,
直线的倾斜角为,斜率,
直线的方程为,代入,
得:,则,,
令,,,,,
则,
四边形是直角梯形,
,
,
抛物线的方程为,
故选:.
4.已知抛物线的焦点为,过的直线交于,两点,点在第一象限,,为坐标原点,则四边形面积最小时直线的方程是
A. B. C. D.
解:抛物线的焦点,设直线的方程为,
联立,可得.
设,,,,,则,
四边形的面积.
令,则,
当时,,单调递减,当时,,单调递增,
当时,即当时,四边形的面积最小,此时,,,
直线的方程为.
故选:.
5.在《西游记》中,凤仙郡太守生气时误推倒祭祀玉帝的贡桌,玉帝一怒之下下令凤仙郡三年不能下雨,于是孙悟空和猪八戒上天庭去找玉帝理论,玉帝要求鸡要吃完米,狗要舔完面,火烧断了锁才能下雨.孙悟空打量着形如圆锥的面山,让猪八戒从面山脚下出发经过的中点到,大致观察一下该面山,如图所示,若猪八戒经过的路线为一条抛物线,,底面圆的面积为,为底面圆的一条直径,则该抛物线的焦点到准线的距离为
A. B. C. D.
解:如图,建立以为轴,过作平行以为轴的直角坐标系,
设抛物线方程为,
底面圆的面积为,所以,,
在中,,
又因为中点,故,
,
,
,
故选:.
6.已知抛物线,直线与交于,两点,若表示直线的斜率,则的最小值为
A.6 B.7 C.8 D.9
解:由抛物线的方程,可得,
所以抛物线的焦点为,
所以直线的方程为经过点,
设,,,,
由,得,
△成立,
所以,
所以,
所以,
因为直线的斜率,
所以,
令,,
则,
当时,,单调递减,
当时,,单调递增,
所以.
所以的最小值为7,
故选:.
7.已知抛物线的焦点为,直线与交于,两点,且,线段的垂直平分线与轴的交点为,则
A. B.2 C. D.
解:设,,,,联立直线与抛物线方程,
,
,
则的垂直平分线为,
则点,
则,
.
故选:.
8.已知抛物线的焦点为,过点斜率为的直线交该抛物线于,在第一象限),直线与圆交于点,在第一象限),为坐标原点,则与的面积之比为
A. B. C. D.
解:由抛物线的方程可得,
则可得直线的方程为:,与抛物线方程联立可得:
,解得,
因为点在第一象限,所以,
所以,,
又由圆的方程可得圆心为,半径,
所以,,
因为三角形的面积为,,
又,四点共线,所以,
所以,
故选:.
多选题
9.已知抛物线的准线方程为,焦点为,为坐标原点,,,,是上两点,则下列说法正确的是
A.点的坐标为
B.若,则的中点到轴距离的最小值为8
C.若直线过点,则以为直径的圆过点
D.若直线与的斜率之积为,则直线过点
解:抛物线的准线方程为,
的解析式为:,
对于:准线方程为,故焦点,故正确;
对于:设,则,
整理得:,故,,故中点为,
,
,,
当且仅当时“”成立,故错误;
对于:设,则,则,
的中点到的距离,
故以为直径的圆不过点,故错误;
对于,
,故,即,过,故正确.
故选:.
10.已知抛物线的准线为,焦点为,原点为,过的直线交抛物线于点、,在第一象限,分别过、作准线的垂线于、,直线的倾斜角为.则下列说法正确的是
A. B.
C.、、三点共线 D.以为直径的圆与轴相切
解:设,,,,
由题意知,直线的方程为,且,
将其与联立,消去得,,
①,②,
,
,即③,
由②③解得,,,
代入①得,,解得,
,,即选项正确;
把,分别代入中,可得,,,,
,
,
由选项可知,,,
,即选项错误;
准线于,,,
,,
、、三点共线,即选项正确;
,,,,
,线段的中点坐标为,
线段的中点横坐标恰为的一半,
以为直径的圆与轴相切,即选项正确.
故选:.
11.已知抛物线的焦点为,准线交轴于点,直线过且交于不同的,两点,在线段上,点为在上的射影,下列命题正确的是
A.若,则
B.若,,三点共线,则
C.若,则
D.对于任意直线,都有
解:如图示:
由题意的焦点为,准线,,
不妨设,联立,则,
即,则,,
设,,,,,
对于,则,,,
整理得:,则,
假设,则直线的斜率为1,
即时,解方程,得,,
故,故错误;
对于:点为在上的射影,则,
,,三点共线时,有,
解得:,,故,,
故,故正确;
对于:作于,由,得,
故,故正确;
对于:由,
而,由,得△,解得:,
故,故正确;
故选:.
12.已知抛物线,过其准线上的点作的两条切线,切点分别为、,下列说法正确的是
A. B.
C.直线的斜率为 D.线段中点的横坐标为1
解:由准线上的点的坐标可得准线方程为,即,
解得,所以不正确;
所以抛物线的方程为;
显然过点的切线的斜率存在且不为0,
设过的切线方程为,
联立,整理可得,
则△,
可得,所以,所以与垂直,所以正确;
设,,,,则,
抛物线的方程,即,所以,
切线的方程为,
即,将点代入可得,
同理切线的方程为,
所以直线的方程为,所以直线的斜率为,所以正确;
中,因为直线的斜率为,
所以,即线段的中点的横坐标为1,所以正确,
故选:.
填空题
13.已知为抛物线的焦点,,点在抛物线上且满足.若这样的点有且只有一个,则实数的值为 .
解:设,,由抛物线的性质,可得,
,,
由,得,把代入,
可得:.
点有且只有一个,方程有两相等实数根.
则△,
整理得,解得.
故答案为:.
14.已知为抛物线的焦点,过作斜率为的直线和抛物线交于,两点,延长,交抛物线于,两点,直线的斜率为.若,则 .
解:设过点作斜率为的直线方程为:,
联立方程,消去可得:,
设,,,,
,
设,,,,
则,同理,
设所在的直线方程为,
联立方程,消去得:,
,同理可得,
则.
15.已知圆,抛物线,抛物线焦点是,过点的直线与抛物线交于点、,与圆交于点、,点、在第一象限,则的最小值是 .
解:由抛物线方程可得,,
当直线的斜率存在时,设的方程为,
代入,整理得,.
设,,,,
,又圆的半径等于1,
,,
因此,
当且仅当,即时等号成立.
当直线的斜率不存在时,可求得.
综上,的最小值为22.
故答案为:22.
16.已知点,为抛物线的焦点,过点且斜率为的直线与抛物线交于,两点,若,则的取值范围是 .
解:由题意知,,设,,,,
直线的方程为,
由,得.
,,
由,得
,
即,解得,
又,,即.
的取值范围是,.
故答案为:,.
同课章节目录
