1.3 中国古代数学中的算法案例
文档属性
| 名称 | 1.3 中国古代数学中的算法案例 |

|
|
| 格式 | zip | ||
| 文件大小 | 131.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-05 00:00:00 | ||
图片预览


文档简介
(共10张PPT)
1.3 算法案例
十进制转换为K进制:
除2取余法
例1 把89化为二进制数
5
2
2
2
1
2
0
1
0
余数
11
22
48
89
2
2
2
2
0
1
1
0
1
注意:1.最后一步商为0, 2.将上式各步所得的余数从下到上排列,得到:89=1011001(2)
分析:采取“满二进一”的原则,可以先解课本中的第一种解法
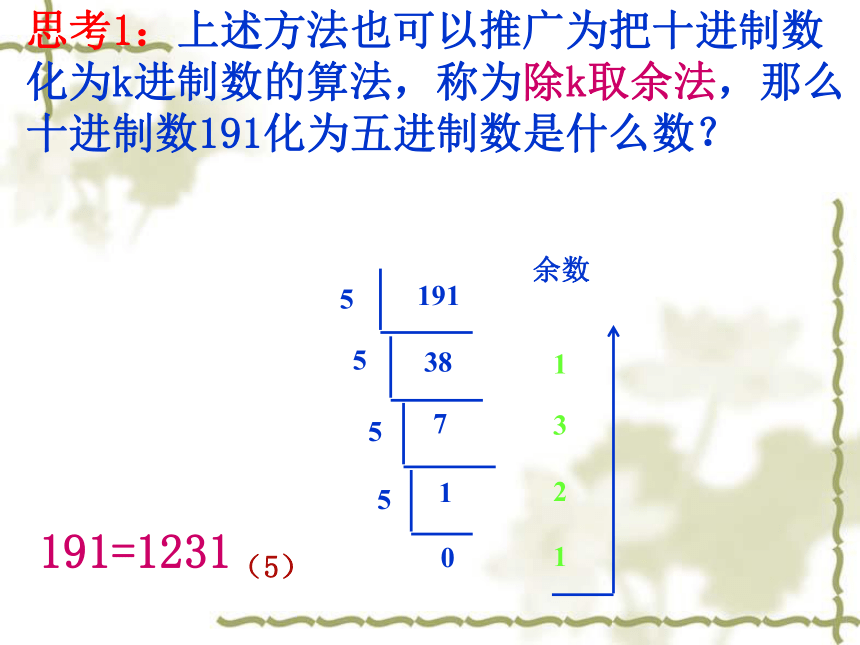
思考1:上述方法也可以推广为把十进制数化为k进制数的算法,称为除k取余法,那么十进制数191化为五进制数是什么数?
0
5
1
5
7
5
38
5
191
1
3
2
1
余数
191=1231(5)
练一练
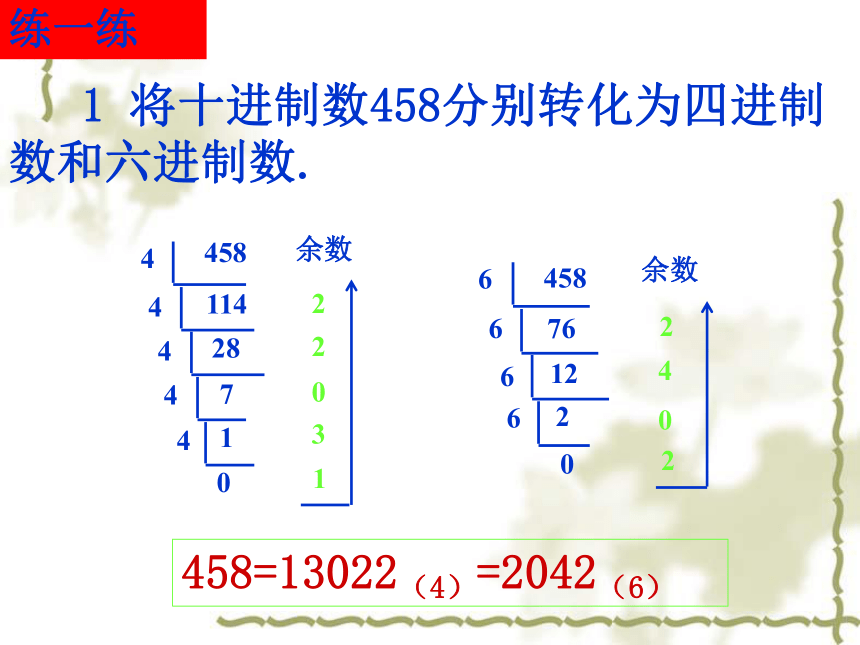
1 将十进制数458分别转化为四进制数和六进制数.
0
4
1
4
7
4
28
4
114
4
458
2
2
0
3
1
余数
0
6
2
6
12
6
76
6
458
2
4
0
2
余数
458=13022(4)=2042(6)
例2 将五进制数3241(5)转化为七进制数.
30241(5)=3×54+2×52+4×5+1=1946.
0
7
5
7
39
7
278
7
1946
0
5
4
5
余数
30241(5)=5450(7)
k进制转换为其它进制
思考2:利用除k取余法,将十进制数a化为k进制数的算法步骤如何设计?
第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的k进制数.
第一步,输入十进制数a和基数k的值.
第二步,求出a除以k所得的商q,余数r.
第三步,把所得的余数依次从右到左排 列.
思考3:将除k取余法的算法步骤用程序框图如何表示?
开始
输入a,k
求a除以k的商q
求a除以k的余数r
把所得的余数依次从右到左排列
a=q
q=0?
结束
输出全部余数r排
列得到的k进制数
是
否
思考4:该程序框图对应的程序如何表述?
开始
输入a,k
求a除以k的商q
求a除以k的余数r
把所得的余数依次从右到左排列
a=q
q=0?
结束
输出全部余数r排
列得到的k进制数
是
否
INPUT a,k
b=0
i=0
DO
q=a/k
r=a MOD k
b=b+r*10∧i
i=i+1
a=q
LOOP UNTIL q=0
PRINT b
END
小结:
1.P45.3 P48.B.1 P50.A.6
2.P48.3 练习册
作业:
1.利用除k取余法,可以把任何一个十进制数化为k进制数,并且操作简单、实用.
.2.通过k进制数与十进制数的转化,我们也可以将一个k进制数转化为另一个不同基数的k进制数.
1.3 算法案例
十进制转换为K进制:
除2取余法
例1 把89化为二进制数
5
2
2
2
1
2
0
1
0
余数
11
22
48
89
2
2
2
2
0
1
1
0
1
注意:1.最后一步商为0, 2.将上式各步所得的余数从下到上排列,得到:89=1011001(2)
分析:采取“满二进一”的原则,可以先解课本中的第一种解法
思考1:上述方法也可以推广为把十进制数化为k进制数的算法,称为除k取余法,那么十进制数191化为五进制数是什么数?
0
5
1
5
7
5
38
5
191
1
3
2
1
余数
191=1231(5)
练一练
1 将十进制数458分别转化为四进制数和六进制数.
0
4
1
4
7
4
28
4
114
4
458
2
2
0
3
1
余数
0
6
2
6
12
6
76
6
458
2
4
0
2
余数
458=13022(4)=2042(6)
例2 将五进制数3241(5)转化为七进制数.
30241(5)=3×54+2×52+4×5+1=1946.
0
7
5
7
39
7
278
7
1946
0
5
4
5
余数
30241(5)=5450(7)
k进制转换为其它进制
思考2:利用除k取余法,将十进制数a化为k进制数的算法步骤如何设计?
第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的k进制数.
第一步,输入十进制数a和基数k的值.
第二步,求出a除以k所得的商q,余数r.
第三步,把所得的余数依次从右到左排 列.
思考3:将除k取余法的算法步骤用程序框图如何表示?
开始
输入a,k
求a除以k的商q
求a除以k的余数r
把所得的余数依次从右到左排列
a=q
q=0?
结束
输出全部余数r排
列得到的k进制数
是
否
思考4:该程序框图对应的程序如何表述?
开始
输入a,k
求a除以k的商q
求a除以k的余数r
把所得的余数依次从右到左排列
a=q
q=0?
结束
输出全部余数r排
列得到的k进制数
是
否
INPUT a,k
b=0
i=0
DO
q=a/k
r=a MOD k
b=b+r*10∧i
i=i+1
a=q
LOOP UNTIL q=0
PRINT b
END
小结:
1.P45.3 P48.B.1 P50.A.6
2.P48.3 练习册
作业:
1.利用除k取余法,可以把任何一个十进制数化为k进制数,并且操作简单、实用.
.2.通过k进制数与十进制数的转化,我们也可以将一个k进制数转化为另一个不同基数的k进制数.
