2020-2021学年上海市黄浦区明珠中学九年级(下)月考数学试卷(3月份)(word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市黄浦区明珠中学九年级(下)月考数学试卷(3月份)(word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 984.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 06:08:49 | ||
图片预览




文档简介
2020-2021学年上海市黄浦区明珠中学九年级(下)月考数学试卷(3月份)
一、选择题(共6小题).
1.下列实数中,无理数是( )
A. B. C.2﹣1 D.()0
2.下列关于x的方程中,一定有实数解的是( )
A. B. C.x2+mx﹣1=0 D.
3.下列对二次函数y=x2﹣x的图象的描述,正确的是( )
A.开口向下
B.对称轴是y轴
C.经过原点
D.在对称轴右侧部分是下降的
4.一次数学作业共有10道题目,某小组8位学生做对题目数的情况如下表:
做对题目数 6 7 8 9 10
人数 1 1 2 3 1
那么这8位学生做对题目数的众数和中位数分别是( )
A.9和8 B.9和8.5 C.3和2 D.3和1
5.在?ABCD中,AC与BD相交于点O,要使四边形ABCD是菱形,还需添加一个条件,这个条件可以是( )
A.AO=CO B.AO=BO C.AO⊥BO D.AB⊥BC
6.下列命题:
①三角形一边的两个端点到这条边上高所在直线的距离相等;
②三角形一边的两个端点到这条边上中线所在直线的距离相等;
③三角形一边的两个端点到这条边所对的角的角平分线所在直线的距离相等.
其中,真命题的个数是( )
A.0个 B.1个 C.2个 D.3个
二、填空题(共12小题).
7.计算的结果是 .
8.计算:(x+y)2﹣x2= .
9.方程组的解是 .
10.某商品原价为a元,如果按原价的八折销售,那么售价是 元.(用含字母a的代数式表示).
11.如果函数y=的图象在每个象限内,当自变量x的值逐渐增大时,y的值随着逐渐增大,那么m的取值范围是 .
12.在植树节当天,某校一个班的学生分成10个小组参加植树造林活动,如果10个小组植树的株数情况见下表,那么这10个小组植树株数的平均数是 株.
植树株数(株) 5 6 7
小组个数 3 4 3
13.从,π,这三个数中选一个数,选出的这个数是无理数的概率为 .
14.如果一次函数y=kx+3(k是常数,k≠0)的图象经过点(﹣1,0),那么y的值随着x的增大而 .(填“增大”或“减小”)
15.在△ABC中,点D在边BC上,且BD:DC=1:2,如果设=,=,那么等于 (结果用、的线性组合表示).
16.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题,如果从某个多边形的一个顶点出发的对角线共有9条,那么该多边形的内角和是 度.
17.在Rt△ABC中,∠C=90°,∠B=70°,点D在边AB上,△ABC绕点D旋转后点B与点C重合,点C落在点C′,那么∠ACC′的度数是 .
18.如图,在Rt△ABC中,∠C=90°,AB=10,sinB=,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为 .
三、解答题:(本大题共7题,满分78分)
19.计算:×(﹣1)2++﹣()﹣1.
20.解方程:﹣=.
21.已知:如图,⊙O的半径为5,P为⊙O外一点,PB、PD与⊙O分别交于点A、B和点C、D,且PO平分∠BPD.
(1)求证:CB=AD;
(2)当PA=1,∠BPO=45°时,求弦AB的长.
22.货车在公路A处加满油后,以每小时60千米的速度匀速行驶,前往与A处相距360千米的B处.下表记录的是货车一次加满油后油箱剩余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x(时) 0 1 2 3 4
余油量y(升) 150 120 90 60 30
(1)如果y关于x的函数是一次函数,求这个函数解析式(不要求写出自变量的取值范围)
(2)在(1)的条件下,如果货车的行驶速度和每小时的耗油量都不变,货车行驶4小时后到达C处,C的前方12千米的D处有一加油站,那么在D处至少加多少升油,才能使货车到达B处卸货后能顺利返回会D处加油?(根据驾驶经验,为保险起见,油箱内剩余油量应随时不少于10升)
23.如图,四边形ABCD是矩形,E是对角线AC上的一点,EB=ED且∠ABE=∠ADE.
(1)求证:四边形ABCD是正方形;
(2)延长DE交BC于点F,交AB的延长线于点G,求证:EF?AG=BC?BE.
24.已知在平面直角坐标系xOy中(如图),已知抛物线y=﹣x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.
(1)求这条抛物线的表达式和点B的坐标;
(2)点M在对称轴上,且位于顶点上方,设它的纵坐标为m,联结AM,用含m的代数式表示∠AMB的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点C在x轴上.原抛物线上一点P平移后的对应点为点Q,如果OP=OQ,求点Q的坐标.
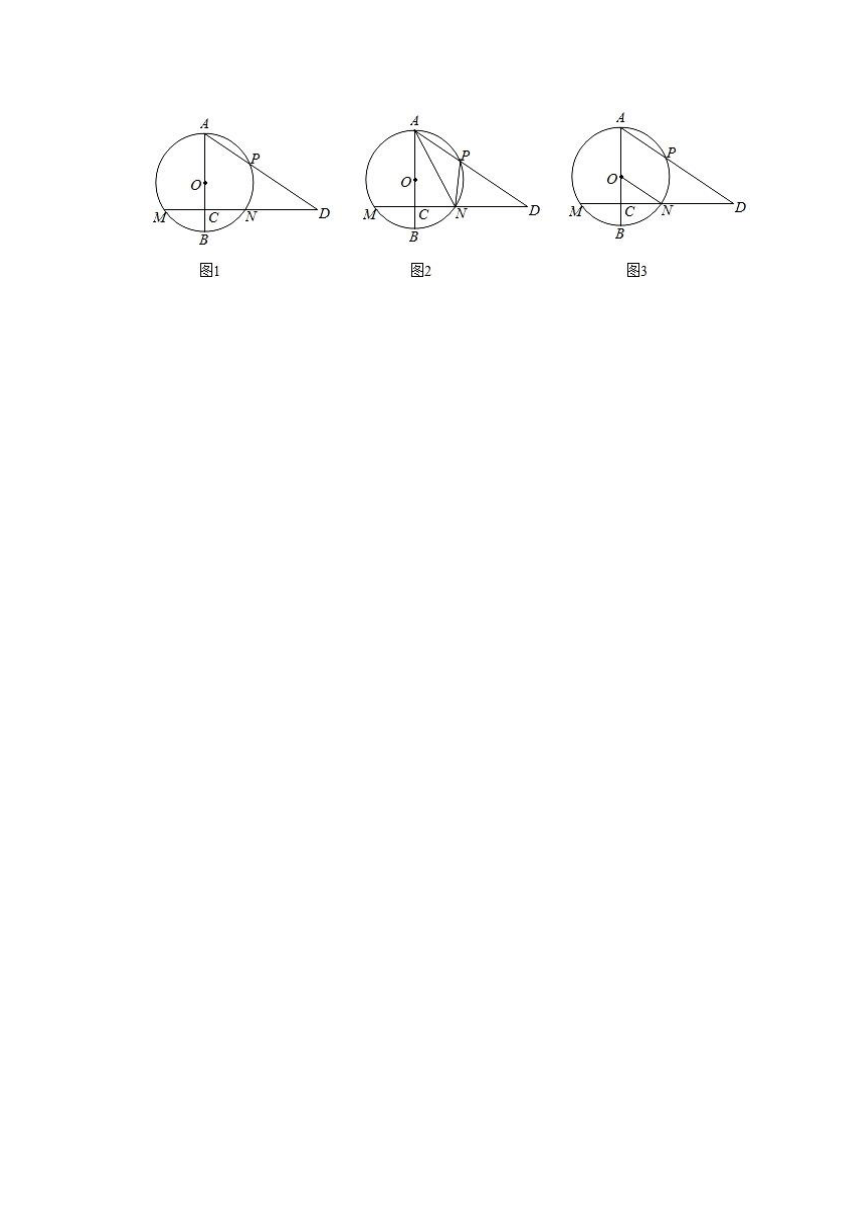
25.如图,已知AB是⊙O的直径,AB=8,点C在半径OB上(点C与点O、B不重合),过点C作AB的垂线交⊙O于点M、N,P为弧AN上一点,射线AP交射线MN于点D.
(1)若P、N是弧AB的三等分点,求DN的长;
(2)如果OC=3,联结AN、PN,当点P是弧AN的中点时,求△ANP的面积与△AND的面积比;
(3)当ON∥AD时,设点C关于直线ON的对称点为Q,若△APQ为等腰三角形,求OC的长.
参考答案
一、选择题(共6小题).
1.下列实数中,无理数是( )
A. B. C.2﹣1 D.()0
解:A,为分数是有理数不符合题意.
B,是无理数符合题意.
C,2﹣1为分数是有理数不符合题意.
D,1为整数是有理数不符合题意.
故选:B.
2.下列关于x的方程中,一定有实数解的是( )
A. B. C.x2+mx﹣1=0 D.
解:∵,∴无解,故选项A错误;
∵,得x﹣1=x2,∴x2﹣x+1=0,则△=(﹣1)2﹣4×1×1=1﹣4=﹣3<0,故此方程无解,故选项B错误;
∵x2+mx﹣1=0,∴△=m2﹣4×1×(﹣1)=m2+4>0,∴x2+mx﹣1=0一定有两个不相等的实数根,故选项C正确;
∵,解得,x=1,而x=1时,x﹣1=0,故此分式方程无解,故选项D错误;
故选:C.
3.下列对二次函数y=x2﹣x的图象的描述,正确的是( )
A.开口向下
B.对称轴是y轴
C.经过原点
D.在对称轴右侧部分是下降的
解:A、∵a=1>0,
∴抛物线开口向上,选项A不正确;
B、∵﹣=,
∴抛物线的对称轴为直线x=,选项B不正确;
C、当x=0时,y=x2﹣x=0,
∴抛物线经过原点,选项C正确;
D、∵a>0,抛物线的对称轴为直线x=,
∴当x>时,y随x值的增大而增大,选项D不正确.
故选:C.
4.一次数学作业共有10道题目,某小组8位学生做对题目数的情况如下表:
做对题目数 6 7 8 9 10
人数 1 1 2 3 1
那么这8位学生做对题目数的众数和中位数分别是( )
A.9和8 B.9和8.5 C.3和2 D.3和1
解:根据图表可得:9出现了3次,出现的次数最多,则众数是9;
把这些数据从小到大排列,最中间的两个数是第4、5个数的平均数,
则这8位学生做对题目数的中位数是:=8.5;
故选:B.
5.在?ABCD中,AC与BD相交于点O,要使四边形ABCD是菱形,还需添加一个条件,这个条件可以是( )
A.AO=CO B.AO=BO C.AO⊥BO D.AB⊥BC
解:添加AO⊥BO,
理由是:∵四边形ABCD是平行四边形,AO⊥BO,
∴?ABCD为菱形,
只有选项C正确;选项A、B、D都错误;
故选:C.
6.下列命题:
①三角形一边的两个端点到这条边上高所在直线的距离相等;
②三角形一边的两个端点到这条边上中线所在直线的距离相等;
③三角形一边的两个端点到这条边所对的角的角平分线所在直线的距离相等.
其中,真命题的个数是( )
A.0个 B.1个 C.2个 D.3个
解:①三角形一边的两个端点到这条边上高所在直线的距离相等,根据垂直平分线上的点到线段两端点距离相等,故此选项错误;
②三角形一边的两个端点到这条边上中线所在直线的距离相等,利用三角形全等的判定可得出,此命题正确,故此选项正确;
③三角形一边的两个端点到这条边所对的角的角平分线所在直线的距离相等,三角形是一般三角形时,此命题错误,
故正确的有1个,
故选:B.
二、填空题:(本大题共12题,每题4分,满分48分)
7.计算的结果是 2 .
解:原式=3﹣=2.
故答案为:2.
8.计算:(x+y)2﹣x2= 2xy+y2 .
解:(x+y)2﹣x2
=x2+2xy+y2﹣x2
=2xy+y2,
故答案为:2xy+y2.
9.方程组的解是 或 .
解:,
①+②得:x2+2x=3,即(x﹣1)(x+3)=0,
解得:x=1或x=﹣3,
把x=1代入①得:2﹣y=0,即y=2;
把x=﹣3代入①得:﹣6﹣y=0,即y=﹣6,
则方程组的解为或.
故答案为:或.
10.某商品原价为a元,如果按原价的八折销售,那么售价是 0.8a 元.(用含字母a的代数式表示).
解:根据题意知售价为0.8a元,
故答案为:0.8a.
11.如果函数y=的图象在每个象限内,当自变量x的值逐渐增大时,y的值随着逐渐增大,那么m的取值范围是 m< .
解:∵反比例函数的图象在其每个象限内,y随着x的增大而增大,
∴3m﹣1<0,
∴m<.
故答案为m<.
12.在植树节当天,某校一个班的学生分成10个小组参加植树造林活动,如果10个小组植树的株数情况见下表,那么这10个小组植树株数的平均数是 6 株.
植树株数(株) 5 6 7
小组个数 3 4 3
解:这10个小组植树株数的平均数是=6(株),
故答案为:6.
13.从,π,这三个数中选一个数,选出的这个数是无理数的概率为 .
解:∵在,π,这三个数中,无理数有π,这2个,
∴选出的这个数是无理数的概率为,
故答案为:.
14.如果一次函数y=kx+3(k是常数,k≠0)的图象经过点(﹣1,0),那么y的值随着x的增大而 增大 .(填“增大”或“减小”)
解:∵一次函数y=kx+3(k是常数,k≠0)的图象经过点(﹣1,0),
∴0=﹣k+3,
∴k=3,
∴y的值随x的增大而增大.
故答案为:增大.
15.在△ABC中,点D在边BC上,且BD:DC=1:2,如果设=,=,那么等于 (结果用、的线性组合表示).
解:如图,∵=,=,
∴=+=﹣,
∵BD=BC,
∴=.
故答案为.
16.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题,如果从某个多边形的一个顶点出发的对角线共有9条,那么该多边形的内角和是 1800 度.
解:∵多边形的一个顶点出发的对角线共有(n﹣3)条,
∴n﹣3=9,
∴n=12,
∴该多边形的边数是12,
∴内角和=(12﹣2)×180°=1800°,
故答案是:1800.
17.在Rt△ABC中,∠C=90°,∠B=70°,点D在边AB上,△ABC绕点D旋转后点B与点C重合,点C落在点C′,那么∠ACC′的度数是 50° .
解:如图所示,∵△ABC绕点D旋转后点B与点C重合,
∴DB=DC,
又∵∠B=70°,∠ACB=90°,
∴∠BCD=70°,∠ACD=90°﹣70°=20°,
由旋转可得,∠B=∠A'CC'=70°,
∴∠ACC'=70°﹣20°=50°.
故答案为:50°.
18.如图,在Rt△ABC中,∠C=90°,AB=10,sinB=,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为 4或8 .
解:Rt△ABC中,∠C=90°,AB=10,sinB=,
∴AC=8,BC==6,
①如图1,当A′D∥BC,
∴∠A′DB=∠B,
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴A′D=AD,∴∠A′=∠A,
∴∠A′+∠A′DB=90°,
∴A′C⊥AB,
∴CE==,
∴A′E=,
∵A′D∥BC,
∴△A′DE∽△CBE,
∴=,即=,
∴A′D=4,
∴AD=4;
②如图2,当A′D∥AC,
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴AD=A′D,AC=A′C,∠ACD=∠A′CD,
∵∠A′DC=∠ACD,
∴∠A′DC=∠A′CD,
∴A′D=A′C,
∴AD=AC=8,
综上所述:AD的长为:4或8.
三、解答题:(本大题共7题,满分78分)
19.计算:×(﹣1)2++﹣()﹣1.
解:原式=
=
=3.
20.解方程:﹣=.
解:去分母得:(x+1)2﹣2=x﹣1,
整理得:x2+x=0,即x(x+1)=0,
解得:x=0或x=﹣1,
经检验x=﹣1是增根,分式方程的解为x=0.
21.已知:如图,⊙O的半径为5,P为⊙O外一点,PB、PD与⊙O分别交于点A、B和点C、D,且PO平分∠BPD.
(1)求证:CB=AD;
(2)当PA=1,∠BPO=45°时,求弦AB的长.
【解答】(1)证明:作OE⊥AB于E,OF⊥CD于F,连接OB,OD,BC,AD,如图,
∵PO平分∠BPD,OE⊥AB,OF⊥CD,
∴OE=OF,AE=BE,CF=DF,
在Rt△OBE和Rt△ODF中,
,
∴Rt△OBE≌Rt△ODF(HL),
∴BE=DF,
∴AB=CD,
∴=,
∴+=+,
即=,
∴AD=BC.
(2)解:在Rt△POE中,∵∠BPO=45°,
∴△POE为等腰直角三角形,
∴OE=PE=PA+AE=1+AE,
而AE=BE,
∴OE=1+BE,
在Rt△BOE中,∵OE2+BE2=OB2,
∴(1+BE)2+BE2=52,解得BE=﹣4(舍去)或BE=3,
∴AB=2BE=6.
22.货车在公路A处加满油后,以每小时60千米的速度匀速行驶,前往与A处相距360千米的B处.下表记录的是货车一次加满油后油箱剩余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x(时) 0 1 2 3 4
余油量y(升) 150 120 90 60 30
(1)如果y关于x的函数是一次函数,求这个函数解析式(不要求写出自变量的取值范围)
(2)在(1)的条件下,如果货车的行驶速度和每小时的耗油量都不变,货车行驶4小时后到达C处,C的前方12千米的D处有一加油站,那么在D处至少加多少升油,才能使货车到达B处卸货后能顺利返回会D处加油?(根据驾驶经验,为保险起见,油箱内剩余油量应随时不少于10升)
解:(1)把5组数据在直角坐标系中描出来,这5个点在一条直线上,所以y与x满足一次函数关系,
设y=kx+b,(k≠0)
则,
解得:,
∴y=﹣30x+150.
(2)设在D处至少加W升油,根据题意得:
150﹣4×30﹣×30+W≥×30×2+10
即:150﹣120﹣6+W≥118
解得W≥94,
答:D处至少加94升油,才能使货车到达灾区B地卸物后能顺利返回D处加油.
23.如图,四边形ABCD是矩形,E是对角线AC上的一点,EB=ED且∠ABE=∠ADE.
(1)求证:四边形ABCD是正方形;
(2)延长DE交BC于点F,交AB的延长线于点G,求证:EF?AG=BC?BE.
【解答】(1)证明:连接BD.
∵EB=ED,
∴∠EBD=∠EDB,
∵∠ABE=∠ADE,
∴∠ABD=∠ADB,
∴AB=AD,
∵四边形ABCD是矩形,
∴四边形ABCD是正方形.
(2)证明:∵四边形ABCD是矩形
∴AD∥BC,
∴,
同理 ,
∵DE=BE,四边形ABCD是正方形,
∴BC=DC,
∴,
∴EF?AG=BC?BE.
24.已知在平面直角坐标系xOy中(如图),已知抛物线y=﹣x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.
(1)求这条抛物线的表达式和点B的坐标;
(2)点M在对称轴上,且位于顶点上方,设它的纵坐标为m,联结AM,用含m的代数式表示∠AMB的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点C在x轴上.原抛物线上一点P平移后的对应点为点Q,如果OP=OQ,求点Q的坐标.
解:(1)∵抛物线的对称轴为x=1,
∴x=﹣=1,即=1,解得b=2.
∴y=﹣x2+2x+c.
将A(2,2)代入得:﹣4+4+c=2,解得:c=2.
∴抛物线的解析式为y=﹣x2+2x+2.
配方得:y=﹣(x﹣1)2+3.
∴抛物线的顶点坐标为(1,3).
(2)如图所示:过点A作AG⊥BM,垂足为G,则AG=1,G(1,2).
∵M(1,m),G(1,2),
∴MG=m﹣2.
∴cot∠AMB==m﹣2.
(3)∵抛物线的顶点坐标为(1,3),平移后抛物线的顶点坐标在x轴上,
∴抛物线向下平移了3个单位.
∴平移后抛物线的解析式为y=﹣x2+2x﹣1,PQ=3.
∵OP=OQ,
∴点O在PQ的垂直平分线上.
又∵QP∥y轴,
∴点Q与点P关于x轴对称.
∴点Q的纵坐标为﹣.
将y=﹣代入y=﹣x2+2x﹣1得:﹣x2+2x﹣1=﹣,解得:x=或x=.
∴点Q的坐标为(,﹣)或(,﹣).
25.如图,已知AB是⊙O的直径,AB=8,点C在半径OB上(点C与点O、B不重合),过点C作AB的垂线交⊙O于点M、N,P为弧AN上一点,射线AP交射线MN于点D.
(1)若P、N是弧AB的三等分点,求DN的长;
(2)如果OC=3,联结AN、PN,当点P是弧AN的中点时,求△ANP的面积与△AND的面积比;
(3)当ON∥AD时,设点C关于直线ON的对称点为Q,若△APQ为等腰三角形,求OC的长.
解:(1)如图1,连接OP,ON,
∵P、N是弧AB的三等分点,AB是⊙O的直径,
∴∠AOP=∠PON=∠CON=60°,
∵OA=OP,
∴△AOP是等边三角形,
∴∠A=∠AOP=60°,
∵AB⊥MN,
∴∠OCN=90°,
Rt△OCN中,∠CNO=30°,ON=AB=4,
∴OC=2,CN=2,
Rt△ACD中,∠D=30°,AC=4+2=6,
∴CD=6,
∴DN=CD﹣CN=6﹣2=4;
(2)如图2,连接ON,OP,OP交AN于点F,
∵P是的中点,
∴OP⊥AN,
Rt△OCN中,ON=4,OC=3,
∴CN==,AN==2,
∴AF=,
由勾股定理得:OF==,
∴PF=4﹣,
过点D作DE⊥AN于点E,
∵∠ACN=∠DEN=90°,∠ANC=∠DNE,
∴△ACN∽△DEN,
∴,即,
∴=,
设DE=x,EN=x,
∵PF⊥AN,DE⊥AN,
∴PF∥DE,
∴△AFP∽△AED,
∴,即=,
解得:x=,
∴DE=x=7,
∴===;
(3)分三种情况:
①当AP=AQ时,如图3,连接OQ,CQ,BP,BP交MN于K,交ON于L,过点A作AE⊥PQ于E,
∵AB是⊙O的直径,
∴∠APB=90°,
∵ON∥AD,
∴∠CON=∠CAP,
∵∠APB=∠OCN=90°,
∴△OCN∽△APB,
∴∠CBP=∠CNO,,即,
∴==,
∴PB=2CN,AP=2OC,
设OC=a,则AP=2a,
∵∠CKB=∠NKL,
∴∠BCK=∠NLK=90°,
∴BP⊥ON,
∴PL=BL=CN,
连接OP,
∵OP=OB,
∴∠POL=∠BOL,
∵点C关于直线ON的对称点为Q,
∴ON是CQ的垂直平分线,
∴OC=OQ=a,
∴∠COL=∠QON,
∴O、Q、P三点共线,
∵AP=AQ,AE⊥PQ,
∴EQ=PE=,
∵OA=OP,
∴∠OAP=∠OPA=∠CON,
∵cos∠OPA==,即,
解得:a1=﹣(舍),a2=,
∴OC=;
②当AQ=PQ时,如图4,连接OQ并延长交AP于点E,连接OP,
∵AQ=PQ,OA=OP,
∴OE是AP的垂直平分线,
∴OE⊥AD,
∵AD∥ON,
∴OE⊥ON,
由(1)知:∠CON=∠EON=90°,
所以此种情况不符合题意;
③当AP=PQ时,如图5,过点P作PF⊥AQ于F,连接OQ,
由①可知:O、Q、P三点共线,OQ=OC=a,AP=PQ=2a,
∵OP=4,
∴a+2a=4,
∴a=,
∴OC=,
综上,OC的长为或.
一、选择题(共6小题).
1.下列实数中,无理数是( )
A. B. C.2﹣1 D.()0
2.下列关于x的方程中,一定有实数解的是( )
A. B. C.x2+mx﹣1=0 D.
3.下列对二次函数y=x2﹣x的图象的描述,正确的是( )
A.开口向下
B.对称轴是y轴
C.经过原点
D.在对称轴右侧部分是下降的
4.一次数学作业共有10道题目,某小组8位学生做对题目数的情况如下表:
做对题目数 6 7 8 9 10
人数 1 1 2 3 1
那么这8位学生做对题目数的众数和中位数分别是( )
A.9和8 B.9和8.5 C.3和2 D.3和1
5.在?ABCD中,AC与BD相交于点O,要使四边形ABCD是菱形,还需添加一个条件,这个条件可以是( )
A.AO=CO B.AO=BO C.AO⊥BO D.AB⊥BC
6.下列命题:
①三角形一边的两个端点到这条边上高所在直线的距离相等;
②三角形一边的两个端点到这条边上中线所在直线的距离相等;
③三角形一边的两个端点到这条边所对的角的角平分线所在直线的距离相等.
其中,真命题的个数是( )
A.0个 B.1个 C.2个 D.3个
二、填空题(共12小题).
7.计算的结果是 .
8.计算:(x+y)2﹣x2= .
9.方程组的解是 .
10.某商品原价为a元,如果按原价的八折销售,那么售价是 元.(用含字母a的代数式表示).
11.如果函数y=的图象在每个象限内,当自变量x的值逐渐增大时,y的值随着逐渐增大,那么m的取值范围是 .
12.在植树节当天,某校一个班的学生分成10个小组参加植树造林活动,如果10个小组植树的株数情况见下表,那么这10个小组植树株数的平均数是 株.
植树株数(株) 5 6 7
小组个数 3 4 3
13.从,π,这三个数中选一个数,选出的这个数是无理数的概率为 .
14.如果一次函数y=kx+3(k是常数,k≠0)的图象经过点(﹣1,0),那么y的值随着x的增大而 .(填“增大”或“减小”)
15.在△ABC中,点D在边BC上,且BD:DC=1:2,如果设=,=,那么等于 (结果用、的线性组合表示).
16.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题,如果从某个多边形的一个顶点出发的对角线共有9条,那么该多边形的内角和是 度.
17.在Rt△ABC中,∠C=90°,∠B=70°,点D在边AB上,△ABC绕点D旋转后点B与点C重合,点C落在点C′,那么∠ACC′的度数是 .
18.如图,在Rt△ABC中,∠C=90°,AB=10,sinB=,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为 .
三、解答题:(本大题共7题,满分78分)
19.计算:×(﹣1)2++﹣()﹣1.
20.解方程:﹣=.
21.已知:如图,⊙O的半径为5,P为⊙O外一点,PB、PD与⊙O分别交于点A、B和点C、D,且PO平分∠BPD.
(1)求证:CB=AD;
(2)当PA=1,∠BPO=45°时,求弦AB的长.
22.货车在公路A处加满油后,以每小时60千米的速度匀速行驶,前往与A处相距360千米的B处.下表记录的是货车一次加满油后油箱剩余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x(时) 0 1 2 3 4
余油量y(升) 150 120 90 60 30
(1)如果y关于x的函数是一次函数,求这个函数解析式(不要求写出自变量的取值范围)
(2)在(1)的条件下,如果货车的行驶速度和每小时的耗油量都不变,货车行驶4小时后到达C处,C的前方12千米的D处有一加油站,那么在D处至少加多少升油,才能使货车到达B处卸货后能顺利返回会D处加油?(根据驾驶经验,为保险起见,油箱内剩余油量应随时不少于10升)
23.如图,四边形ABCD是矩形,E是对角线AC上的一点,EB=ED且∠ABE=∠ADE.
(1)求证:四边形ABCD是正方形;
(2)延长DE交BC于点F,交AB的延长线于点G,求证:EF?AG=BC?BE.
24.已知在平面直角坐标系xOy中(如图),已知抛物线y=﹣x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.
(1)求这条抛物线的表达式和点B的坐标;
(2)点M在对称轴上,且位于顶点上方,设它的纵坐标为m,联结AM,用含m的代数式表示∠AMB的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点C在x轴上.原抛物线上一点P平移后的对应点为点Q,如果OP=OQ,求点Q的坐标.
25.如图,已知AB是⊙O的直径,AB=8,点C在半径OB上(点C与点O、B不重合),过点C作AB的垂线交⊙O于点M、N,P为弧AN上一点,射线AP交射线MN于点D.
(1)若P、N是弧AB的三等分点,求DN的长;
(2)如果OC=3,联结AN、PN,当点P是弧AN的中点时,求△ANP的面积与△AND的面积比;
(3)当ON∥AD时,设点C关于直线ON的对称点为Q,若△APQ为等腰三角形,求OC的长.
参考答案
一、选择题(共6小题).
1.下列实数中,无理数是( )
A. B. C.2﹣1 D.()0
解:A,为分数是有理数不符合题意.
B,是无理数符合题意.
C,2﹣1为分数是有理数不符合题意.
D,1为整数是有理数不符合题意.
故选:B.
2.下列关于x的方程中,一定有实数解的是( )
A. B. C.x2+mx﹣1=0 D.
解:∵,∴无解,故选项A错误;
∵,得x﹣1=x2,∴x2﹣x+1=0,则△=(﹣1)2﹣4×1×1=1﹣4=﹣3<0,故此方程无解,故选项B错误;
∵x2+mx﹣1=0,∴△=m2﹣4×1×(﹣1)=m2+4>0,∴x2+mx﹣1=0一定有两个不相等的实数根,故选项C正确;
∵,解得,x=1,而x=1时,x﹣1=0,故此分式方程无解,故选项D错误;
故选:C.
3.下列对二次函数y=x2﹣x的图象的描述,正确的是( )
A.开口向下
B.对称轴是y轴
C.经过原点
D.在对称轴右侧部分是下降的
解:A、∵a=1>0,
∴抛物线开口向上,选项A不正确;
B、∵﹣=,
∴抛物线的对称轴为直线x=,选项B不正确;
C、当x=0时,y=x2﹣x=0,
∴抛物线经过原点,选项C正确;
D、∵a>0,抛物线的对称轴为直线x=,
∴当x>时,y随x值的增大而增大,选项D不正确.
故选:C.
4.一次数学作业共有10道题目,某小组8位学生做对题目数的情况如下表:
做对题目数 6 7 8 9 10
人数 1 1 2 3 1
那么这8位学生做对题目数的众数和中位数分别是( )
A.9和8 B.9和8.5 C.3和2 D.3和1
解:根据图表可得:9出现了3次,出现的次数最多,则众数是9;
把这些数据从小到大排列,最中间的两个数是第4、5个数的平均数,
则这8位学生做对题目数的中位数是:=8.5;
故选:B.
5.在?ABCD中,AC与BD相交于点O,要使四边形ABCD是菱形,还需添加一个条件,这个条件可以是( )
A.AO=CO B.AO=BO C.AO⊥BO D.AB⊥BC
解:添加AO⊥BO,
理由是:∵四边形ABCD是平行四边形,AO⊥BO,
∴?ABCD为菱形,
只有选项C正确;选项A、B、D都错误;
故选:C.
6.下列命题:
①三角形一边的两个端点到这条边上高所在直线的距离相等;
②三角形一边的两个端点到这条边上中线所在直线的距离相等;
③三角形一边的两个端点到这条边所对的角的角平分线所在直线的距离相等.
其中,真命题的个数是( )
A.0个 B.1个 C.2个 D.3个
解:①三角形一边的两个端点到这条边上高所在直线的距离相等,根据垂直平分线上的点到线段两端点距离相等,故此选项错误;
②三角形一边的两个端点到这条边上中线所在直线的距离相等,利用三角形全等的判定可得出,此命题正确,故此选项正确;
③三角形一边的两个端点到这条边所对的角的角平分线所在直线的距离相等,三角形是一般三角形时,此命题错误,
故正确的有1个,
故选:B.
二、填空题:(本大题共12题,每题4分,满分48分)
7.计算的结果是 2 .
解:原式=3﹣=2.
故答案为:2.
8.计算:(x+y)2﹣x2= 2xy+y2 .
解:(x+y)2﹣x2
=x2+2xy+y2﹣x2
=2xy+y2,
故答案为:2xy+y2.
9.方程组的解是 或 .
解:,
①+②得:x2+2x=3,即(x﹣1)(x+3)=0,
解得:x=1或x=﹣3,
把x=1代入①得:2﹣y=0,即y=2;
把x=﹣3代入①得:﹣6﹣y=0,即y=﹣6,
则方程组的解为或.
故答案为:或.
10.某商品原价为a元,如果按原价的八折销售,那么售价是 0.8a 元.(用含字母a的代数式表示).
解:根据题意知售价为0.8a元,
故答案为:0.8a.
11.如果函数y=的图象在每个象限内,当自变量x的值逐渐增大时,y的值随着逐渐增大,那么m的取值范围是 m< .
解:∵反比例函数的图象在其每个象限内,y随着x的增大而增大,
∴3m﹣1<0,
∴m<.
故答案为m<.
12.在植树节当天,某校一个班的学生分成10个小组参加植树造林活动,如果10个小组植树的株数情况见下表,那么这10个小组植树株数的平均数是 6 株.
植树株数(株) 5 6 7
小组个数 3 4 3
解:这10个小组植树株数的平均数是=6(株),
故答案为:6.
13.从,π,这三个数中选一个数,选出的这个数是无理数的概率为 .
解:∵在,π,这三个数中,无理数有π,这2个,
∴选出的这个数是无理数的概率为,
故答案为:.
14.如果一次函数y=kx+3(k是常数,k≠0)的图象经过点(﹣1,0),那么y的值随着x的增大而 增大 .(填“增大”或“减小”)
解:∵一次函数y=kx+3(k是常数,k≠0)的图象经过点(﹣1,0),
∴0=﹣k+3,
∴k=3,
∴y的值随x的增大而增大.
故答案为:增大.
15.在△ABC中,点D在边BC上,且BD:DC=1:2,如果设=,=,那么等于 (结果用、的线性组合表示).
解:如图,∵=,=,
∴=+=﹣,
∵BD=BC,
∴=.
故答案为.
16.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题,如果从某个多边形的一个顶点出发的对角线共有9条,那么该多边形的内角和是 1800 度.
解:∵多边形的一个顶点出发的对角线共有(n﹣3)条,
∴n﹣3=9,
∴n=12,
∴该多边形的边数是12,
∴内角和=(12﹣2)×180°=1800°,
故答案是:1800.
17.在Rt△ABC中,∠C=90°,∠B=70°,点D在边AB上,△ABC绕点D旋转后点B与点C重合,点C落在点C′,那么∠ACC′的度数是 50° .
解:如图所示,∵△ABC绕点D旋转后点B与点C重合,
∴DB=DC,
又∵∠B=70°,∠ACB=90°,
∴∠BCD=70°,∠ACD=90°﹣70°=20°,
由旋转可得,∠B=∠A'CC'=70°,
∴∠ACC'=70°﹣20°=50°.
故答案为:50°.
18.如图,在Rt△ABC中,∠C=90°,AB=10,sinB=,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为 4或8 .
解:Rt△ABC中,∠C=90°,AB=10,sinB=,
∴AC=8,BC==6,
①如图1,当A′D∥BC,
∴∠A′DB=∠B,
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴A′D=AD,∴∠A′=∠A,
∴∠A′+∠A′DB=90°,
∴A′C⊥AB,
∴CE==,
∴A′E=,
∵A′D∥BC,
∴△A′DE∽△CBE,
∴=,即=,
∴A′D=4,
∴AD=4;
②如图2,当A′D∥AC,
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴AD=A′D,AC=A′C,∠ACD=∠A′CD,
∵∠A′DC=∠ACD,
∴∠A′DC=∠A′CD,
∴A′D=A′C,
∴AD=AC=8,
综上所述:AD的长为:4或8.
三、解答题:(本大题共7题,满分78分)
19.计算:×(﹣1)2++﹣()﹣1.
解:原式=
=
=3.
20.解方程:﹣=.
解:去分母得:(x+1)2﹣2=x﹣1,
整理得:x2+x=0,即x(x+1)=0,
解得:x=0或x=﹣1,
经检验x=﹣1是增根,分式方程的解为x=0.
21.已知:如图,⊙O的半径为5,P为⊙O外一点,PB、PD与⊙O分别交于点A、B和点C、D,且PO平分∠BPD.
(1)求证:CB=AD;
(2)当PA=1,∠BPO=45°时,求弦AB的长.
【解答】(1)证明:作OE⊥AB于E,OF⊥CD于F,连接OB,OD,BC,AD,如图,
∵PO平分∠BPD,OE⊥AB,OF⊥CD,
∴OE=OF,AE=BE,CF=DF,
在Rt△OBE和Rt△ODF中,
,
∴Rt△OBE≌Rt△ODF(HL),
∴BE=DF,
∴AB=CD,
∴=,
∴+=+,
即=,
∴AD=BC.
(2)解:在Rt△POE中,∵∠BPO=45°,
∴△POE为等腰直角三角形,
∴OE=PE=PA+AE=1+AE,
而AE=BE,
∴OE=1+BE,
在Rt△BOE中,∵OE2+BE2=OB2,
∴(1+BE)2+BE2=52,解得BE=﹣4(舍去)或BE=3,
∴AB=2BE=6.
22.货车在公路A处加满油后,以每小时60千米的速度匀速行驶,前往与A处相距360千米的B处.下表记录的是货车一次加满油后油箱剩余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x(时) 0 1 2 3 4
余油量y(升) 150 120 90 60 30
(1)如果y关于x的函数是一次函数,求这个函数解析式(不要求写出自变量的取值范围)
(2)在(1)的条件下,如果货车的行驶速度和每小时的耗油量都不变,货车行驶4小时后到达C处,C的前方12千米的D处有一加油站,那么在D处至少加多少升油,才能使货车到达B处卸货后能顺利返回会D处加油?(根据驾驶经验,为保险起见,油箱内剩余油量应随时不少于10升)
解:(1)把5组数据在直角坐标系中描出来,这5个点在一条直线上,所以y与x满足一次函数关系,
设y=kx+b,(k≠0)
则,
解得:,
∴y=﹣30x+150.
(2)设在D处至少加W升油,根据题意得:
150﹣4×30﹣×30+W≥×30×2+10
即:150﹣120﹣6+W≥118
解得W≥94,
答:D处至少加94升油,才能使货车到达灾区B地卸物后能顺利返回D处加油.
23.如图,四边形ABCD是矩形,E是对角线AC上的一点,EB=ED且∠ABE=∠ADE.
(1)求证:四边形ABCD是正方形;
(2)延长DE交BC于点F,交AB的延长线于点G,求证:EF?AG=BC?BE.
【解答】(1)证明:连接BD.
∵EB=ED,
∴∠EBD=∠EDB,
∵∠ABE=∠ADE,
∴∠ABD=∠ADB,
∴AB=AD,
∵四边形ABCD是矩形,
∴四边形ABCD是正方形.
(2)证明:∵四边形ABCD是矩形
∴AD∥BC,
∴,
同理 ,
∵DE=BE,四边形ABCD是正方形,
∴BC=DC,
∴,
∴EF?AG=BC?BE.
24.已知在平面直角坐标系xOy中(如图),已知抛物线y=﹣x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.
(1)求这条抛物线的表达式和点B的坐标;
(2)点M在对称轴上,且位于顶点上方,设它的纵坐标为m,联结AM,用含m的代数式表示∠AMB的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点C在x轴上.原抛物线上一点P平移后的对应点为点Q,如果OP=OQ,求点Q的坐标.
解:(1)∵抛物线的对称轴为x=1,
∴x=﹣=1,即=1,解得b=2.
∴y=﹣x2+2x+c.
将A(2,2)代入得:﹣4+4+c=2,解得:c=2.
∴抛物线的解析式为y=﹣x2+2x+2.
配方得:y=﹣(x﹣1)2+3.
∴抛物线的顶点坐标为(1,3).
(2)如图所示:过点A作AG⊥BM,垂足为G,则AG=1,G(1,2).
∵M(1,m),G(1,2),
∴MG=m﹣2.
∴cot∠AMB==m﹣2.
(3)∵抛物线的顶点坐标为(1,3),平移后抛物线的顶点坐标在x轴上,
∴抛物线向下平移了3个单位.
∴平移后抛物线的解析式为y=﹣x2+2x﹣1,PQ=3.
∵OP=OQ,
∴点O在PQ的垂直平分线上.
又∵QP∥y轴,
∴点Q与点P关于x轴对称.
∴点Q的纵坐标为﹣.
将y=﹣代入y=﹣x2+2x﹣1得:﹣x2+2x﹣1=﹣,解得:x=或x=.
∴点Q的坐标为(,﹣)或(,﹣).
25.如图,已知AB是⊙O的直径,AB=8,点C在半径OB上(点C与点O、B不重合),过点C作AB的垂线交⊙O于点M、N,P为弧AN上一点,射线AP交射线MN于点D.
(1)若P、N是弧AB的三等分点,求DN的长;
(2)如果OC=3,联结AN、PN,当点P是弧AN的中点时,求△ANP的面积与△AND的面积比;
(3)当ON∥AD时,设点C关于直线ON的对称点为Q,若△APQ为等腰三角形,求OC的长.
解:(1)如图1,连接OP,ON,
∵P、N是弧AB的三等分点,AB是⊙O的直径,
∴∠AOP=∠PON=∠CON=60°,
∵OA=OP,
∴△AOP是等边三角形,
∴∠A=∠AOP=60°,
∵AB⊥MN,
∴∠OCN=90°,
Rt△OCN中,∠CNO=30°,ON=AB=4,
∴OC=2,CN=2,
Rt△ACD中,∠D=30°,AC=4+2=6,
∴CD=6,
∴DN=CD﹣CN=6﹣2=4;
(2)如图2,连接ON,OP,OP交AN于点F,
∵P是的中点,
∴OP⊥AN,
Rt△OCN中,ON=4,OC=3,
∴CN==,AN==2,
∴AF=,
由勾股定理得:OF==,
∴PF=4﹣,
过点D作DE⊥AN于点E,
∵∠ACN=∠DEN=90°,∠ANC=∠DNE,
∴△ACN∽△DEN,
∴,即,
∴=,
设DE=x,EN=x,
∵PF⊥AN,DE⊥AN,
∴PF∥DE,
∴△AFP∽△AED,
∴,即=,
解得:x=,
∴DE=x=7,
∴===;
(3)分三种情况:
①当AP=AQ时,如图3,连接OQ,CQ,BP,BP交MN于K,交ON于L,过点A作AE⊥PQ于E,
∵AB是⊙O的直径,
∴∠APB=90°,
∵ON∥AD,
∴∠CON=∠CAP,
∵∠APB=∠OCN=90°,
∴△OCN∽△APB,
∴∠CBP=∠CNO,,即,
∴==,
∴PB=2CN,AP=2OC,
设OC=a,则AP=2a,
∵∠CKB=∠NKL,
∴∠BCK=∠NLK=90°,
∴BP⊥ON,
∴PL=BL=CN,
连接OP,
∵OP=OB,
∴∠POL=∠BOL,
∵点C关于直线ON的对称点为Q,
∴ON是CQ的垂直平分线,
∴OC=OQ=a,
∴∠COL=∠QON,
∴O、Q、P三点共线,
∵AP=AQ,AE⊥PQ,
∴EQ=PE=,
∵OA=OP,
∴∠OAP=∠OPA=∠CON,
∵cos∠OPA==,即,
解得:a1=﹣(舍),a2=,
∴OC=;
②当AQ=PQ时,如图4,连接OQ并延长交AP于点E,连接OP,
∵AQ=PQ,OA=OP,
∴OE是AP的垂直平分线,
∴OE⊥AD,
∵AD∥ON,
∴OE⊥ON,
由(1)知:∠CON=∠EON=90°,
所以此种情况不符合题意;
③当AP=PQ时,如图5,过点P作PF⊥AQ于F,连接OQ,
由①可知:O、Q、P三点共线,OQ=OC=a,AP=PQ=2a,
∵OP=4,
∴a+2a=4,
∴a=,
∴OC=,
综上,OC的长为或.
同课章节目录
