2.1 曲线与方程
图片预览








文档简介
(共26张PPT)
曲线和方程
—— 1.曲线和方程
(1)、求第一、三象限里两轴间夹角平分线的坐标满足的关系
第一、三象限角平分线
点的横坐标与纵坐标相等
x=y(或x-y=0)
得出关系:
x-y=0
x
y
0
(1)
上点的坐标都是方程x-y=0的解
(2)以方程x-y=0的解为坐标的点都在 上
曲线
条件
方程
分析特例归纳定义
曲线和方程之间有什么对应关系呢?
(2)、函数
的图象是关于y轴对称的抛物线
这条抛物线的方程是
·
0
x
y
M
满足关系:
(1)、如果
是抛物线上的点,那么
一定是这个方程的解
(2)、如果
是方程
的解,那么以它为坐标的点一定
在抛物线上
分析特例归纳定义
(3)、说明过A(2,0)平行于y轴的直线与方程︱x︱=2的关系
①、直线上的点的坐标都满足方程︱x︱=2
②、满足方程︱x︱=2的点不一定在直线上
结论:过A(2,0)平行于y轴的直线的方程不是︱x︱=2
0
x
y
2
A
分析特例归纳定义
给定曲线C与二元方程f(x,y)=0,若满足
(1)曲线上的点坐标都是这个方程的解
(2)以这个方程的解为坐标的点都是曲线上的点
那么这个方程f(x,y)=0叫做这条曲线C的方程
这条曲线C叫做这个方程的曲线
定义
说明:1、曲线的方程——反映的是图形所满足的数量关系
方程的曲线——反映的是数量关系所表示的图形
f(x,y)=0
0
x
y
分析特例归纳定义
2、两者间的关系:点在曲线上
点的坐标适合于此曲线的方程
通俗地说:无点不是解且无解不是点 或说点不 比解多且解也不比点多
即:曲线上所有点的集合与此曲线的方程的解集能够一一对应
3、如果曲线C的方程是f(x,y)=0,那么点
在曲线C上的充要条件
是
集合的观点
例1判断下列结论的正误并说明理由
(1)过点A(3,0)且垂直于x轴的直线为x=3
(2)到x轴距离为2的点的轨迹方程为y=2
(3)到两坐标轴距离乘积等于1的点的轨迹方程为xy=1
对
错
错
例2证明:圆心为坐标原点,半径为5的圆的方程是
并判断
是否在圆上
变式训练:写出下列半圆的方程
0
x
y
5
5
·
·
学习例题巩固定义
y
y
y
-5
y
5
5
5
5
5
5
5
-5
-5
-5
-5
0
0
x
x
x
x
(1)举出一个方程与曲线,使 它们之间的关系符合①而不符合②.
(2)举出一个方程与曲线,使 它们之间的关系符合② 而不符合① .
(3) 举出一个方程与曲线,使 它们之间的关系既符合①又符合②。
变式思维训练,深化理解
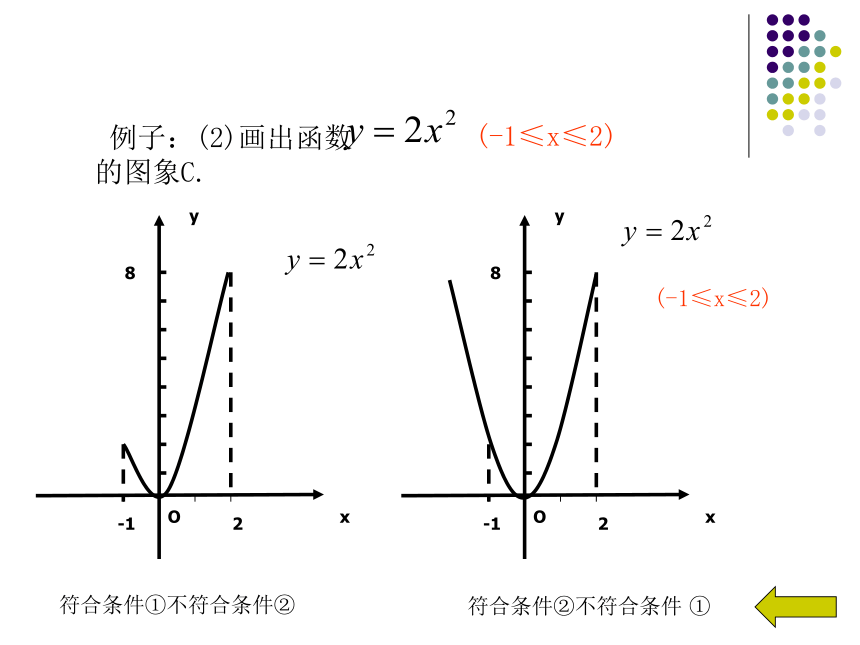
例子:(2)画出函数 的图象C.
(-1≤x≤2)
(-1≤x≤2)
x
8
2
-1
y
O
x
8
2
-1
y
O
符合条件①不符合条件②
符合条件②不符合条件 ①
例子:(2)画出函数 的图象C.
(-1≤x≤2)
(-1≤x≤2)
x
8
2
-1
y
O
符合条件①、 ②
下列各题中,图3表示的曲线方程是所列出的方程吗?如果不是,不符合定义中的关系①还是关系②?
(1)曲线C为过点A(1,1),B(-1,1)的折线,方程为(x-y)(x+y)=0;
(2)曲线C是顶点在原点的抛物线,方程为x+ =0;
(3)曲线C是Ⅰ, Ⅱ象限内到X轴,Y轴的距离乘积为1的点集,方程为y= 。
1
0
x
y
-1
1
0
x
y
-1
1
-2
2
1
0
x
y
-1
1
-2
2
1
图3
例2 证明以坐标原点为圆心,半径等于5的圆的方程是x2 +y2 = 25,并判断点M1(3,-4),M2(-3,2)是否在这个圆上.
证明:(1)设M(x0,y0)是圆上任意一点.因为点M到坐标原点的距离等于5,所以
也就是xo2 +yo2 = 25.
即 (x0,y0) 是方程x2 +y2 = 25的解.
(2)设 (x0,y0) 是方程x2 +y2 = 25的解,那么
x02 +y02 = 25
两边开方取算术根,得
即点M (x0,y0)到坐标原点的距离等于5,点M (x0,y0)是这个圆上的一点.
由1、2可知, x2 +y2 = 25,是以坐标原点为圆心,半径等于5的圆的方程.
第一步,设M (x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;
归纳:
证明已知曲线的方程的方法和步骤
第二步,设(x0,y0)是f(x,y)=0的解,证明点M (x0,y0)在曲线C上.
小结
在轨迹的基础上将轨迹和条件化为曲线和方程,当说某方程是曲线的方程或某曲线是方程的曲线时就意味着具备上述两个条件,只有具备上述两个方面的要求,才能将曲线的研究化为方程的研究,几何问题化为代数问题,以数助形正是解析几何的思想,本节课正是这一思想的基础。
曲线和方程(2)
复习与引入
线段的垂直平分线的性质是怎样的
曲线的方程和方程的曲线的定义是怎样的
例题讲解
例1 设A、B两点坐标是(-1,-1)、(3,7),求线段AB的垂直平分线方程。
分析:1、题中设了A、B两点坐标,说明题
中已给定了坐标系。
2、由线段的垂直平分线的性质
可知,适合题意的几何等量关系
为:︱MA︱=︱MB︱。
3、设动点M(x,y),其目的是由形
向数转化。
4、由两点间的距离公式代换
︱MA︱=︱MB︱后,并合理化简。
5、根据曲线的方程的定义,在求出线段AB的垂直平分线方程后要证明曲线方程的完备性。
X
Y
O
3
-3
7
A
B
M
例1 设A、B两点坐标是(-1,-1)、(3,7),求线段AB的垂直平分线方程。
解:设M(x,y)是线段AB的垂直平分线上任意一点,则点M属于集合
P={M︱︱MA︱=︱MB︱}.
由两点间的距离公式,点M所适合的条件可表示为
将上式两边平方,整理得
x+2y-7=0 (1)
下面证明方程x+2y-7=0是线段平分线的方程.
(1)由求方程的过程中可知,垂直平分线上每一点的坐标都是方程(1)的解;
(2)设点M1的坐标(x1,y1)是方程(1)的解,即 x1+2y1-7=0,也就是x1=7-2y1.
点M1到A(-1,-1),B(3,7)的距离分别为
即点M1在线段AB的垂直平分线上.
由(1),(2)知,方程(1)是线段AB的垂直平分线的方程.
例2 点M与两互相垂直的直线的距离的积是常数k(k>0),求点M的轨迹方程.
解:取已知两互相垂直的直线为坐标轴,建立直角坐标系,如图所示.
设点M的坐标为(x,y).点M的
轨迹就是与坐标轴的距离的积等于
常数k的点的集合
P={M︱︱MR︱·︱MQ︱=k},
其中Q,R分别是点M到x轴,y轴的
垂线的垂足.即
︱x︱·︱y︱=k,即
xy=±k.
O
M
R
Q
X
Y
下面证明方程xy=±k (1)就是所求轨迹的方程.
(1)由求方程的过程可知,曲线上的点的坐标都是方程(1)的解;
(2)设点M1的坐标(x1,y1)是方程(1)的解,那么
x1y1=±k,
即 ︱x1︱·︱y1︱=k,
而︱x1︱,︱y1︱正是点M1到纵轴,横轴的距离,因此点M1到这两条直线的距离的积是常数k,即点M1是曲线上的点.
由(1),(2)可知,方程(1)是所求轨迹的方程.
求曲线方程的一般步骤:
建立适当的坐标系,用实数对,例如(x,y)表示曲线上任意一点M的坐标(注意建立坐标系的基本原则)---建系设点;
写出适合条件p的点M的集合P={M︱p(M)}---列式;
用坐标表示条件p(M),列出方程f(x,y)=0---代换.;
化方程f(x,y)=0为最简形式---化简;
证明以化简后的方程的截为坐标的点都是曲线上的点---证明.
一般情况下,化简前后方程的解集是相同的,步骤(5)可以省略不写.如有特殊情况,可适当予以说明,另外,根据情况,也可以省略步骤(2),直接列出方程.
课堂练习:课本第72页练习1,2.
补充:1.定长为2a的线段,其两端点分别在x轴和y轴上滑动,求该线段中点所形成的曲线方程.
2.已知线段AB的长为10,动点P到A,B的距离的平方和为122,求动点P的轨迹方程.
x2+y2=36
课堂小结:
1.求曲线方程的一般步骤.
2.建立适当坐标系的方法:
(1)定点、定线段选在坐标轴上;
(2)原点有时选在定点;
(3)充分利用对称性,坐标轴可选为对称轴。
X2+y2=a2.
曲线和方程
—— 1.曲线和方程
(1)、求第一、三象限里两轴间夹角平分线的坐标满足的关系
第一、三象限角平分线
点的横坐标与纵坐标相等
x=y(或x-y=0)
得出关系:
x-y=0
x
y
0
(1)
上点的坐标都是方程x-y=0的解
(2)以方程x-y=0的解为坐标的点都在 上
曲线
条件
方程
分析特例归纳定义
曲线和方程之间有什么对应关系呢?
(2)、函数
的图象是关于y轴对称的抛物线
这条抛物线的方程是
·
0
x
y
M
满足关系:
(1)、如果
是抛物线上的点,那么
一定是这个方程的解
(2)、如果
是方程
的解,那么以它为坐标的点一定
在抛物线上
分析特例归纳定义
(3)、说明过A(2,0)平行于y轴的直线与方程︱x︱=2的关系
①、直线上的点的坐标都满足方程︱x︱=2
②、满足方程︱x︱=2的点不一定在直线上
结论:过A(2,0)平行于y轴的直线的方程不是︱x︱=2
0
x
y
2
A
分析特例归纳定义
给定曲线C与二元方程f(x,y)=0,若满足
(1)曲线上的点坐标都是这个方程的解
(2)以这个方程的解为坐标的点都是曲线上的点
那么这个方程f(x,y)=0叫做这条曲线C的方程
这条曲线C叫做这个方程的曲线
定义
说明:1、曲线的方程——反映的是图形所满足的数量关系
方程的曲线——反映的是数量关系所表示的图形
f(x,y)=0
0
x
y
分析特例归纳定义
2、两者间的关系:点在曲线上
点的坐标适合于此曲线的方程
通俗地说:无点不是解且无解不是点 或说点不 比解多且解也不比点多
即:曲线上所有点的集合与此曲线的方程的解集能够一一对应
3、如果曲线C的方程是f(x,y)=0,那么点
在曲线C上的充要条件
是
集合的观点
例1判断下列结论的正误并说明理由
(1)过点A(3,0)且垂直于x轴的直线为x=3
(2)到x轴距离为2的点的轨迹方程为y=2
(3)到两坐标轴距离乘积等于1的点的轨迹方程为xy=1
对
错
错
例2证明:圆心为坐标原点,半径为5的圆的方程是
并判断
是否在圆上
变式训练:写出下列半圆的方程
0
x
y
5
5
·
·
学习例题巩固定义
y
y
y
-5
y
5
5
5
5
5
5
5
-5
-5
-5
-5
0
0
x
x
x
x
(1)举出一个方程与曲线,使 它们之间的关系符合①而不符合②.
(2)举出一个方程与曲线,使 它们之间的关系符合② 而不符合① .
(3) 举出一个方程与曲线,使 它们之间的关系既符合①又符合②。
变式思维训练,深化理解
例子:(2)画出函数 的图象C.
(-1≤x≤2)
(-1≤x≤2)
x
8
2
-1
y
O
x
8
2
-1
y
O
符合条件①不符合条件②
符合条件②不符合条件 ①
例子:(2)画出函数 的图象C.
(-1≤x≤2)
(-1≤x≤2)
x
8
2
-1
y
O
符合条件①、 ②
下列各题中,图3表示的曲线方程是所列出的方程吗?如果不是,不符合定义中的关系①还是关系②?
(1)曲线C为过点A(1,1),B(-1,1)的折线,方程为(x-y)(x+y)=0;
(2)曲线C是顶点在原点的抛物线,方程为x+ =0;
(3)曲线C是Ⅰ, Ⅱ象限内到X轴,Y轴的距离乘积为1的点集,方程为y= 。
1
0
x
y
-1
1
0
x
y
-1
1
-2
2
1
0
x
y
-1
1
-2
2
1
图3
例2 证明以坐标原点为圆心,半径等于5的圆的方程是x2 +y2 = 25,并判断点M1(3,-4),M2(-3,2)是否在这个圆上.
证明:(1)设M(x0,y0)是圆上任意一点.因为点M到坐标原点的距离等于5,所以
也就是xo2 +yo2 = 25.
即 (x0,y0) 是方程x2 +y2 = 25的解.
(2)设 (x0,y0) 是方程x2 +y2 = 25的解,那么
x02 +y02 = 25
两边开方取算术根,得
即点M (x0,y0)到坐标原点的距离等于5,点M (x0,y0)是这个圆上的一点.
由1、2可知, x2 +y2 = 25,是以坐标原点为圆心,半径等于5的圆的方程.
第一步,设M (x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;
归纳:
证明已知曲线的方程的方法和步骤
第二步,设(x0,y0)是f(x,y)=0的解,证明点M (x0,y0)在曲线C上.
小结
在轨迹的基础上将轨迹和条件化为曲线和方程,当说某方程是曲线的方程或某曲线是方程的曲线时就意味着具备上述两个条件,只有具备上述两个方面的要求,才能将曲线的研究化为方程的研究,几何问题化为代数问题,以数助形正是解析几何的思想,本节课正是这一思想的基础。
曲线和方程(2)
复习与引入
线段的垂直平分线的性质是怎样的
曲线的方程和方程的曲线的定义是怎样的
例题讲解
例1 设A、B两点坐标是(-1,-1)、(3,7),求线段AB的垂直平分线方程。
分析:1、题中设了A、B两点坐标,说明题
中已给定了坐标系。
2、由线段的垂直平分线的性质
可知,适合题意的几何等量关系
为:︱MA︱=︱MB︱。
3、设动点M(x,y),其目的是由形
向数转化。
4、由两点间的距离公式代换
︱MA︱=︱MB︱后,并合理化简。
5、根据曲线的方程的定义,在求出线段AB的垂直平分线方程后要证明曲线方程的完备性。
X
Y
O
3
-3
7
A
B
M
例1 设A、B两点坐标是(-1,-1)、(3,7),求线段AB的垂直平分线方程。
解:设M(x,y)是线段AB的垂直平分线上任意一点,则点M属于集合
P={M︱︱MA︱=︱MB︱}.
由两点间的距离公式,点M所适合的条件可表示为
将上式两边平方,整理得
x+2y-7=0 (1)
下面证明方程x+2y-7=0是线段平分线的方程.
(1)由求方程的过程中可知,垂直平分线上每一点的坐标都是方程(1)的解;
(2)设点M1的坐标(x1,y1)是方程(1)的解,即 x1+2y1-7=0,也就是x1=7-2y1.
点M1到A(-1,-1),B(3,7)的距离分别为
即点M1在线段AB的垂直平分线上.
由(1),(2)知,方程(1)是线段AB的垂直平分线的方程.
例2 点M与两互相垂直的直线的距离的积是常数k(k>0),求点M的轨迹方程.
解:取已知两互相垂直的直线为坐标轴,建立直角坐标系,如图所示.
设点M的坐标为(x,y).点M的
轨迹就是与坐标轴的距离的积等于
常数k的点的集合
P={M︱︱MR︱·︱MQ︱=k},
其中Q,R分别是点M到x轴,y轴的
垂线的垂足.即
︱x︱·︱y︱=k,即
xy=±k.
O
M
R
Q
X
Y
下面证明方程xy=±k (1)就是所求轨迹的方程.
(1)由求方程的过程可知,曲线上的点的坐标都是方程(1)的解;
(2)设点M1的坐标(x1,y1)是方程(1)的解,那么
x1y1=±k,
即 ︱x1︱·︱y1︱=k,
而︱x1︱,︱y1︱正是点M1到纵轴,横轴的距离,因此点M1到这两条直线的距离的积是常数k,即点M1是曲线上的点.
由(1),(2)可知,方程(1)是所求轨迹的方程.
求曲线方程的一般步骤:
建立适当的坐标系,用实数对,例如(x,y)表示曲线上任意一点M的坐标(注意建立坐标系的基本原则)---建系设点;
写出适合条件p的点M的集合P={M︱p(M)}---列式;
用坐标表示条件p(M),列出方程f(x,y)=0---代换.;
化方程f(x,y)=0为最简形式---化简;
证明以化简后的方程的截为坐标的点都是曲线上的点---证明.
一般情况下,化简前后方程的解集是相同的,步骤(5)可以省略不写.如有特殊情况,可适当予以说明,另外,根据情况,也可以省略步骤(2),直接列出方程.
课堂练习:课本第72页练习1,2.
补充:1.定长为2a的线段,其两端点分别在x轴和y轴上滑动,求该线段中点所形成的曲线方程.
2.已知线段AB的长为10,动点P到A,B的距离的平方和为122,求动点P的轨迹方程.
x2+y2=36
课堂小结:
1.求曲线方程的一般步骤.
2.建立适当坐标系的方法:
(1)定点、定线段选在坐标轴上;
(2)原点有时选在定点;
(3)充分利用对称性,坐标轴可选为对称轴。
X2+y2=a2.
