2.3 双曲线
图片预览









文档简介
(共43张PPT)
双曲线及其标准方程
一、回顾
1、椭圆的定义是什么?
2、椭圆的标准方程、焦点坐标是什么?
平面上到两个定点的距离的和等于定长2a(2a大于| |)的点的轨迹叫椭圆。
x2
a2
+
y2
b2
=
1
( a >0,b >0)
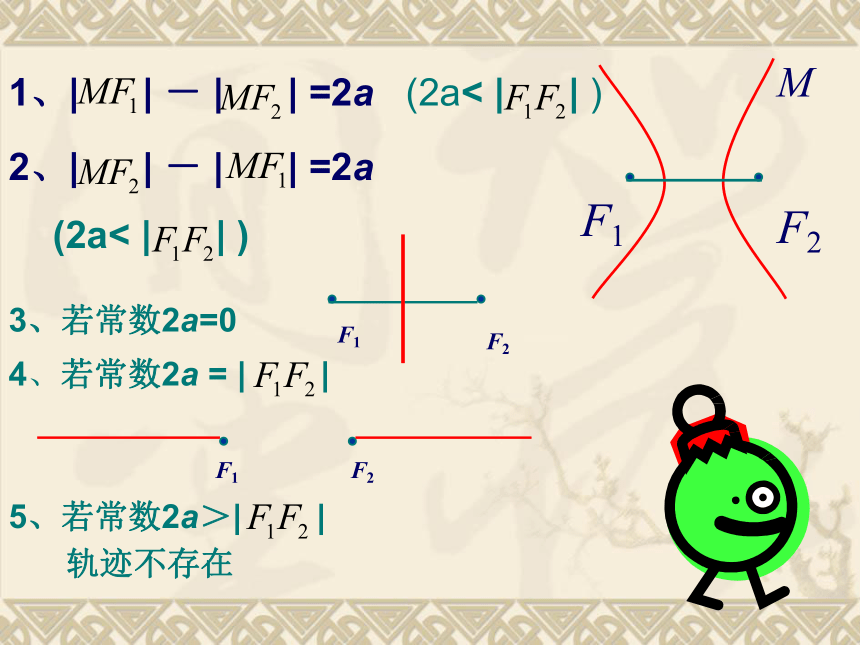
想一想:如果“和”改为“差”,曲线的轨迹是什么?
F1
2、| | - | | =2a
1、| | - | | =2a
(2a< | | )
(2a< | | )
F2
M
这两条曲线合起来叫做双曲线,
每一条叫做双曲线的一支。
双曲线的定义
平面内与两定点F1,F2的距离的差的绝对值等于常数(小于|F1F2 | )的点的轨迹叫做双曲线。
注意: 1. 为什么要强调差的绝对值?
2. 为什么这个常数要小于|F1F2 |?如果不小于|F1F2 | ,轨迹是什么?
这两个定点叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距。
F1
F2
M
2、| | - | | =2a
1、| | - | | =2a
(2a< | | )
(2a< | | )
3、若常数2a=0
4、若常数2a = | |
F1
F2
5、若常数2a>| |
F1
F2
轨迹不存在
如何求双曲线的标准方程?
x
y
o
1、建系设点。设M(x , y),双曲线的焦距为2c(c>0),F1(-c,0),F2(c,0)
常数=2a
F1
F2
M
2,双曲线就是集合:
P= {M ||MF1 | - | MF2| = ± 2a }
3.代入坐标,得方程。
即 √(x+c)2+y2 - √(x-c)2 + y2 = ± 2a
cx-a2=± a √(x-c)2+y2
(c2-a2) x2-a2y2=a2(c2-a2)
∵c>a,∴c2 >a2
令(c2-a2)=b2 (b>0)
x2
a2
-
b2
=
1
(a >0,b >0 c2=a2+b2)
y2
这就是焦点在x轴上的双曲线的标准方程
4.化为最简形式.
F1
F2
y
x
o
y2
a2
-
x2
b2
=
1
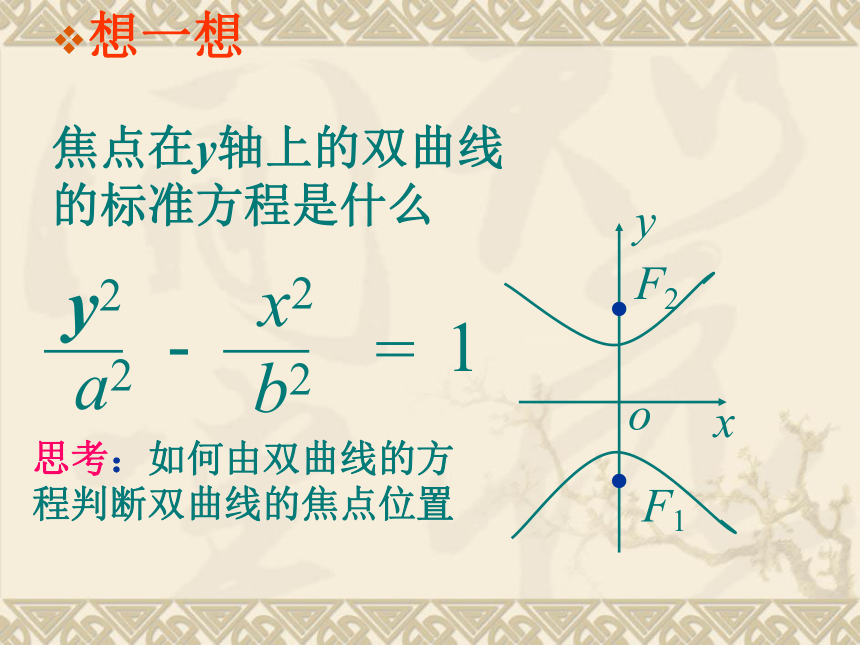
焦点在y轴上的双曲线的标准方程是什么
想一想
思考:如何由双曲线的方程判断双曲线的焦点位置
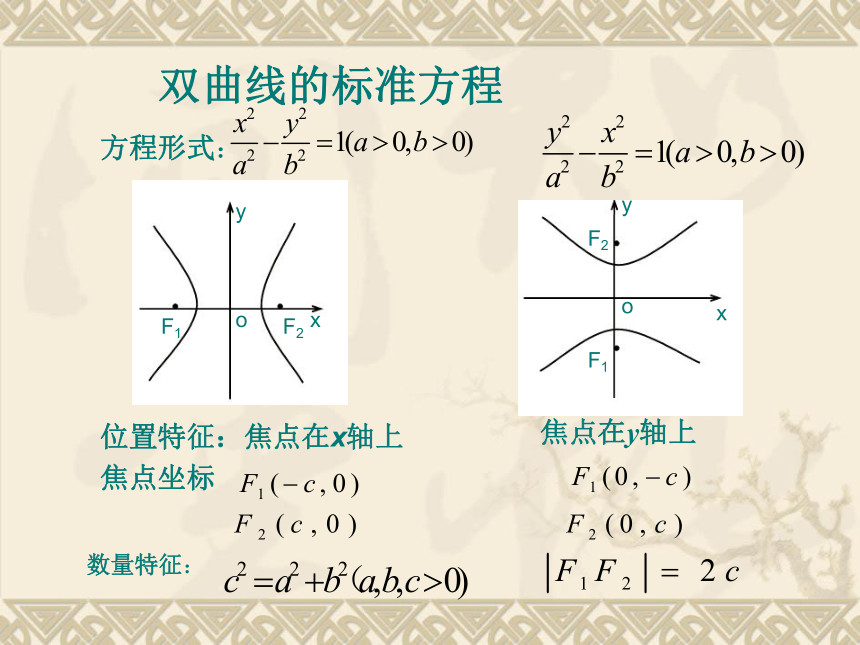
双曲线的标准方程
方程形式:
位置特征:焦点在x轴上
焦点坐标
F1
F2
o
x
y
F1
F2
o
x
y
焦点在y轴上
数量特征:
例题分析
所求轨迹的方程为:
两条射线
轨迹不存在
例1、已知双曲线的焦点 (-5,0), (5,0),双曲线上一点P到焦点的距离差的绝对值等于6,求双曲线的标准方程。
变1、方程表示焦点在x轴上的双曲线时,求m的范围
例2、如果方程 表示双曲线,求m的范围
解(m-1)(2-m)<0,∴m>2或m<1
变2、方程表示焦点在x轴上的椭圆时,求m的范围
x2
y2
m-1
+
2-m
=
1
解: m-1 >0
2-m <0
解: m-1 > 2-m > 0
∴m>2
∴1.5变3、对1、2条件下,求焦点坐标。
解:(± ,0)
双曲线的一支
两条射线
1、平面内与两定点F1,F2的距离的差等于常数(小于 F1F2 )的点的轨迹是什么?
2、若常数2a=0,轨迹是什么
3、若常数2a= F1F2 轨迹是什么?
垂直平分线
4、若常数2a> 轨迹是什么?
轨迹不存在
小结
定义
图像
方程
焦点
a.b.c的关系
·
x2
a2
-
y2
b2
=
1
y2
x2
a2
-
b2
=
1
||MF1|-|MF2||=2a(2a < |F1F2|)
c2=a2+b2
F ( ±c,0) F(0, ± c)
F1
F2
o
x
y
F1
F2
o
x
2、⑴证明椭圆
与双曲线x2-15y2=15的焦点相同
⑵若此椭圆与双曲线的一个交点
为P,F为焦点,求|PF|
1、反比例函数是
双曲线吗?
x2
25
+
y2
9
=
1
课外思考
作业
1. 习题8.3:1、2、
2.预习思考题8.3:3
双曲线的简单几何性质
双曲线的定义
点p到两定点
F1 F2的距离之差
的绝对值为常数(小于F1 F2的距离)点p 的轨迹
X
Y
0
F1
F2
p
Y
X
F1
F2
A1
A2
B1
B2
双曲线图像(1)
双曲线的简单几何性质
标 准 方 程
范 围
对称性
顶 点
焦 点
对称轴
离心率
渐近线
0
双 曲 线 的 范 围
根据双曲线的标准方程
可得: 即 ,所以x≥a, x≤-a
这说明双曲线在不等式
x≥a, x≤-a所表示的区
域内,即在直线x=-a,x=a两侧.
当x的绝对值无限增大时,
y的绝对值也无限增大,所以
曲线是无限伸展的,不像椭圆那样是封闭曲线.
双 曲 线 的 对 称 性:
双曲线关于每个坐标轴和原点都是对称的.坐标轴是双曲线的对称轴,原点是双曲线的对称中心.双曲线的对称中心叫做双曲线的中心.
双 曲 线 的 顶 点:
在双曲线的标准方程中,令y=0得x=±a,因此把A1(-a,0), A2(a,0)叫做双曲线的顶点.
如图:线段A1A2叫做双曲线的实轴,它的长等于2a, a叫做双曲线的实半轴长.
线段B1B2叫做双曲线的虚轴,它的长等于2b, b叫做双曲线的虚半轴长.
双曲线的渐近线
想一想:怎样较为准确的画出
16
9
x
-
y
=1
2
2
的图象 ?
Y
X
-4
4
-3
3
0
猜想:
√
4
3
2
- 4
2
=
4
3
±
±
√
y=
x
1-( )
x
x
4
2
y= ±
4
3
x
y=
4
3
x
y= -
4
3
x
4
3
2
- 4
2
±
√
y=
x
Y
X
F1
F2
A1
A2
B1
B2
0
M
N
第一象限的曲线方程 c :
直线方程:
y=
a
b
x
y= √x
a
b
2
- a
2
( x> a)
C:
设M(x,y) 是c上一点,
y=
a
b
x
N (x,Y)是直线
.
.
上一点。
y =
a
b
x
±
.
Q
双曲线 的渐近线是
MN
= Y- y
=
a
b
( x -
√x – a
2
2
)
x +
√x – a
2
2
ab
=
Y
X
F1
F2
A1
A2
B1
B2
0
M
N
.
.
.
Q
( x -
√x – a
2
2
)
=
a
b
( x -
√x – a
2
2
)
.
( x +
√x – a
2
2
)
( x +
√x – a
2
2
)
>0
x +
√x – a
2
2
ab
双 曲 线 的 离 心 率:
双曲线的焦距与实轴长的比 ,
叫做双曲线的离心率.因为c>a>0,
所以 e>1.
由
c - a = b
2
2
2
c - a
2
2
a
b
=
√
a
2
2
=
√
a
c
- 1
=√
e - 1
2
Y
X
F1
F2
A1
A2
B1
B2
0
a
b
=√
e - 1
2
e越小(接近1)
双曲线开口越小(褊狭)
a
b
越接近0
e越大
a
b
双曲线开口越大(开阔)
越大
双曲线图像与性质(1)
标 准 方 程
范 围
对称性
顶 点
焦 点
对称轴
离心率
渐近线
1
2
2
2
2
=
-
b
y
a
x
x≥a 或x≤-a
关于x轴,y轴,原点对称。
A1(-a,0),A2(a,0)
实轴 A1A2 虚轴 B1B2
F1
(-c , 0 ),
F2
( c , 0 )
a
c
e=
Y
X
F1
F2
A1
A2
B1
B2
0
y =
a
b
x
±
双曲线图像(2)
标 准 方 程
范 围
对称性
顶 点
焦 点
对称轴
离心率
渐近线
X
Y
F1
F2
O
B1
B2
A2
A1
双曲线图像与性质(2)
标 准 方 程
范 围
对称性
顶 点
焦 点
对称轴
离心率
渐近线
y≥a 或y≤-a
关于x轴,y轴,原点对称。
B1(0, -a ),B2(0,a)
实轴 B1B2 虚轴 A1A2
F1
(0 , -c ),
F2
( 0 , c )
a
c
e=
y =
b
a
x
±
1
2
2
2
2
=
-
a
x
b
y
X
Y
F1
F2
O
B1
B2
A2
A1
上述两种双曲线性质对比
标 准 方 程
范 围
对称性
顶 点
焦 点
对称轴
离心率
渐近线
1
2
2
2
2
=
-
b
y
a
x
x≥a 或x≤-a
关于x轴,y轴,原点对称。
A1(-a,0),A2(a,0)
实轴 A1A2 虚轴 B1B2
F1
(-c , 0 ),
F2
( c , 0 )
a
c
e=
y =
a
b
x
±
1
2
2
2
2
=
-
a
x
b
y
y≥a 或y≤-a
关于x轴,y轴,原点对称。
B1(0, -a ),B2(0,a)
F1
(0 , -c ),
F2
( 0 , c )
实轴 B1B2 虚轴 A1A2
a
c
e=
y =
b
a
x
±
例题讲解
例题1 :求双曲线
的实半轴长,虚半轴长,
焦点坐标,离心率.渐近线方程。
解:把方程化为标准方程
可得:实半轴长a=4
虚半轴长b=3
半焦距c=
焦点坐标是(0,-5),(0,5)
离心率:
渐近线方程:
144
16
9
2
2
=
-
x
y
1
3
4
2
2
2
2
=
-
x
y
5
3
4
2
2
=
+
4
5
=
=
a
c
e
1.求下列双曲线的实半轴长和虚半轴长,
(1)
(2)
焦点坐标,顶点坐标,离心率,渐近线的方程.
课 堂 练 习
方 程
图 象
实半轴长
虚半轴 长
焦点坐标
顶点坐 标
离心率
渐近线方程
2. 求顶点在x轴上,两顶点间的距离为8,
离心率e=5/4的双曲线的标准方程.
解:由2a=8, e=5/4
可得a=4 b=3 c=5
因为双曲线的顶点在x轴上,所以它的焦点也在x轴
上,所以它的标准方程为:
练习:
已知双曲线的两条渐进线方程是
焦点坐标是
求此双曲线的方程
例2、双曲线型自然通风塔的外形,是双曲线
的一部分绕其虚轴旋转所成的曲面,它的
最小半径为12m,上口半径为13m,下口半径
为25m,高55m.选择适当的坐标系,求出此
双曲线的方程(精确到1m).
A′
A
0
x
C′
C
B′
B
y
13
12
25
例题讲解
双曲线及其标准方程
一、回顾
1、椭圆的定义是什么?
2、椭圆的标准方程、焦点坐标是什么?
平面上到两个定点的距离的和等于定长2a(2a大于| |)的点的轨迹叫椭圆。
x2
a2
+
y2
b2
=
1
( a >0,b >0)
想一想:如果“和”改为“差”,曲线的轨迹是什么?
F1
2、| | - | | =2a
1、| | - | | =2a
(2a< | | )
(2a< | | )
F2
M
这两条曲线合起来叫做双曲线,
每一条叫做双曲线的一支。
双曲线的定义
平面内与两定点F1,F2的距离的差的绝对值等于常数(小于|F1F2 | )的点的轨迹叫做双曲线。
注意: 1. 为什么要强调差的绝对值?
2. 为什么这个常数要小于|F1F2 |?如果不小于|F1F2 | ,轨迹是什么?
这两个定点叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距。
F1
F2
M
2、| | - | | =2a
1、| | - | | =2a
(2a< | | )
(2a< | | )
3、若常数2a=0
4、若常数2a = | |
F1
F2
5、若常数2a>| |
F1
F2
轨迹不存在
如何求双曲线的标准方程?
x
y
o
1、建系设点。设M(x , y),双曲线的焦距为2c(c>0),F1(-c,0),F2(c,0)
常数=2a
F1
F2
M
2,双曲线就是集合:
P= {M ||MF1 | - | MF2| = ± 2a }
3.代入坐标,得方程。
即 √(x+c)2+y2 - √(x-c)2 + y2 = ± 2a
cx-a2=± a √(x-c)2+y2
(c2-a2) x2-a2y2=a2(c2-a2)
∵c>a,∴c2 >a2
令(c2-a2)=b2 (b>0)
x2
a2
-
b2
=
1
(a >0,b >0 c2=a2+b2)
y2
这就是焦点在x轴上的双曲线的标准方程
4.化为最简形式.
F1
F2
y
x
o
y2
a2
-
x2
b2
=
1
焦点在y轴上的双曲线的标准方程是什么
想一想
思考:如何由双曲线的方程判断双曲线的焦点位置
双曲线的标准方程
方程形式:
位置特征:焦点在x轴上
焦点坐标
F1
F2
o
x
y
F1
F2
o
x
y
焦点在y轴上
数量特征:
例题分析
所求轨迹的方程为:
两条射线
轨迹不存在
例1、已知双曲线的焦点 (-5,0), (5,0),双曲线上一点P到焦点的距离差的绝对值等于6,求双曲线的标准方程。
变1、方程表示焦点在x轴上的双曲线时,求m的范围
例2、如果方程 表示双曲线,求m的范围
解(m-1)(2-m)<0,∴m>2或m<1
变2、方程表示焦点在x轴上的椭圆时,求m的范围
x2
y2
m-1
+
2-m
=
1
解: m-1 >0
2-m <0
解: m-1 > 2-m > 0
∴m>2
∴1.5
解:(± ,0)
双曲线的一支
两条射线
1、平面内与两定点F1,F2的距离的差等于常数(小于 F1F2 )的点的轨迹是什么?
2、若常数2a=0,轨迹是什么
3、若常数2a= F1F2 轨迹是什么?
垂直平分线
4、若常数2a> 轨迹是什么?
轨迹不存在
小结
定义
图像
方程
焦点
a.b.c的关系
·
x2
a2
-
y2
b2
=
1
y2
x2
a2
-
b2
=
1
||MF1|-|MF2||=2a(2a < |F1F2|)
c2=a2+b2
F ( ±c,0) F(0, ± c)
F1
F2
o
x
y
F1
F2
o
x
2、⑴证明椭圆
与双曲线x2-15y2=15的焦点相同
⑵若此椭圆与双曲线的一个交点
为P,F为焦点,求|PF|
1、反比例函数是
双曲线吗?
x2
25
+
y2
9
=
1
课外思考
作业
1. 习题8.3:1、2、
2.预习思考题8.3:3
双曲线的简单几何性质
双曲线的定义
点p到两定点
F1 F2的距离之差
的绝对值为常数(小于F1 F2的距离)点p 的轨迹
X
Y
0
F1
F2
p
Y
X
F1
F2
A1
A2
B1
B2
双曲线图像(1)
双曲线的简单几何性质
标 准 方 程
范 围
对称性
顶 点
焦 点
对称轴
离心率
渐近线
0
双 曲 线 的 范 围
根据双曲线的标准方程
可得: 即 ,所以x≥a, x≤-a
这说明双曲线在不等式
x≥a, x≤-a所表示的区
域内,即在直线x=-a,x=a两侧.
当x的绝对值无限增大时,
y的绝对值也无限增大,所以
曲线是无限伸展的,不像椭圆那样是封闭曲线.
双 曲 线 的 对 称 性:
双曲线关于每个坐标轴和原点都是对称的.坐标轴是双曲线的对称轴,原点是双曲线的对称中心.双曲线的对称中心叫做双曲线的中心.
双 曲 线 的 顶 点:
在双曲线的标准方程中,令y=0得x=±a,因此把A1(-a,0), A2(a,0)叫做双曲线的顶点.
如图:线段A1A2叫做双曲线的实轴,它的长等于2a, a叫做双曲线的实半轴长.
线段B1B2叫做双曲线的虚轴,它的长等于2b, b叫做双曲线的虚半轴长.
双曲线的渐近线
想一想:怎样较为准确的画出
16
9
x
-
y
=1
2
2
的图象 ?
Y
X
-4
4
-3
3
0
猜想:
√
4
3
2
- 4
2
=
4
3
±
±
√
y=
x
1-( )
x
x
4
2
y= ±
4
3
x
y=
4
3
x
y= -
4
3
x
4
3
2
- 4
2
±
√
y=
x
Y
X
F1
F2
A1
A2
B1
B2
0
M
N
第一象限的曲线方程 c :
直线方程:
y=
a
b
x
y= √x
a
b
2
- a
2
( x> a)
C:
设M(x,y) 是c上一点,
y=
a
b
x
N (x,Y)是直线
.
.
上一点。
y =
a
b
x
±
.
Q
双曲线 的渐近线是
MN
= Y- y
=
a
b
( x -
√x – a
2
2
)
x +
√x – a
2
2
ab
=
Y
X
F1
F2
A1
A2
B1
B2
0
M
N
.
.
.
Q
( x -
√x – a
2
2
)
=
a
b
( x -
√x – a
2
2
)
.
( x +
√x – a
2
2
)
( x +
√x – a
2
2
)
>0
x +
√x – a
2
2
ab
双 曲 线 的 离 心 率:
双曲线的焦距与实轴长的比 ,
叫做双曲线的离心率.因为c>a>0,
所以 e>1.
由
c - a = b
2
2
2
c - a
2
2
a
b
=
√
a
2
2
=
√
a
c
- 1
=√
e - 1
2
Y
X
F1
F2
A1
A2
B1
B2
0
a
b
=√
e - 1
2
e越小(接近1)
双曲线开口越小(褊狭)
a
b
越接近0
e越大
a
b
双曲线开口越大(开阔)
越大
双曲线图像与性质(1)
标 准 方 程
范 围
对称性
顶 点
焦 点
对称轴
离心率
渐近线
1
2
2
2
2
=
-
b
y
a
x
x≥a 或x≤-a
关于x轴,y轴,原点对称。
A1(-a,0),A2(a,0)
实轴 A1A2 虚轴 B1B2
F1
(-c , 0 ),
F2
( c , 0 )
a
c
e=
Y
X
F1
F2
A1
A2
B1
B2
0
y =
a
b
x
±
双曲线图像(2)
标 准 方 程
范 围
对称性
顶 点
焦 点
对称轴
离心率
渐近线
X
Y
F1
F2
O
B1
B2
A2
A1
双曲线图像与性质(2)
标 准 方 程
范 围
对称性
顶 点
焦 点
对称轴
离心率
渐近线
y≥a 或y≤-a
关于x轴,y轴,原点对称。
B1(0, -a ),B2(0,a)
实轴 B1B2 虚轴 A1A2
F1
(0 , -c ),
F2
( 0 , c )
a
c
e=
y =
b
a
x
±
1
2
2
2
2
=
-
a
x
b
y
X
Y
F1
F2
O
B1
B2
A2
A1
上述两种双曲线性质对比
标 准 方 程
范 围
对称性
顶 点
焦 点
对称轴
离心率
渐近线
1
2
2
2
2
=
-
b
y
a
x
x≥a 或x≤-a
关于x轴,y轴,原点对称。
A1(-a,0),A2(a,0)
实轴 A1A2 虚轴 B1B2
F1
(-c , 0 ),
F2
( c , 0 )
a
c
e=
y =
a
b
x
±
1
2
2
2
2
=
-
a
x
b
y
y≥a 或y≤-a
关于x轴,y轴,原点对称。
B1(0, -a ),B2(0,a)
F1
(0 , -c ),
F2
( 0 , c )
实轴 B1B2 虚轴 A1A2
a
c
e=
y =
b
a
x
±
例题讲解
例题1 :求双曲线
的实半轴长,虚半轴长,
焦点坐标,离心率.渐近线方程。
解:把方程化为标准方程
可得:实半轴长a=4
虚半轴长b=3
半焦距c=
焦点坐标是(0,-5),(0,5)
离心率:
渐近线方程:
144
16
9
2
2
=
-
x
y
1
3
4
2
2
2
2
=
-
x
y
5
3
4
2
2
=
+
4
5
=
=
a
c
e
1.求下列双曲线的实半轴长和虚半轴长,
(1)
(2)
焦点坐标,顶点坐标,离心率,渐近线的方程.
课 堂 练 习
方 程
图 象
实半轴长
虚半轴 长
焦点坐标
顶点坐 标
离心率
渐近线方程
2. 求顶点在x轴上,两顶点间的距离为8,
离心率e=5/4的双曲线的标准方程.
解:由2a=8, e=5/4
可得a=4 b=3 c=5
因为双曲线的顶点在x轴上,所以它的焦点也在x轴
上,所以它的标准方程为:
练习:
已知双曲线的两条渐进线方程是
焦点坐标是
求此双曲线的方程
例2、双曲线型自然通风塔的外形,是双曲线
的一部分绕其虚轴旋转所成的曲面,它的
最小半径为12m,上口半径为13m,下口半径
为25m,高55m.选择适当的坐标系,求出此
双曲线的方程(精确到1m).
A′
A
0
x
C′
C
B′
B
y
13
12
25
例题讲解
