3.1 空间向量及其运算
图片预览






文档简介
(共73张PPT)
山东省临沂第二中学
———共线向量与共面向量
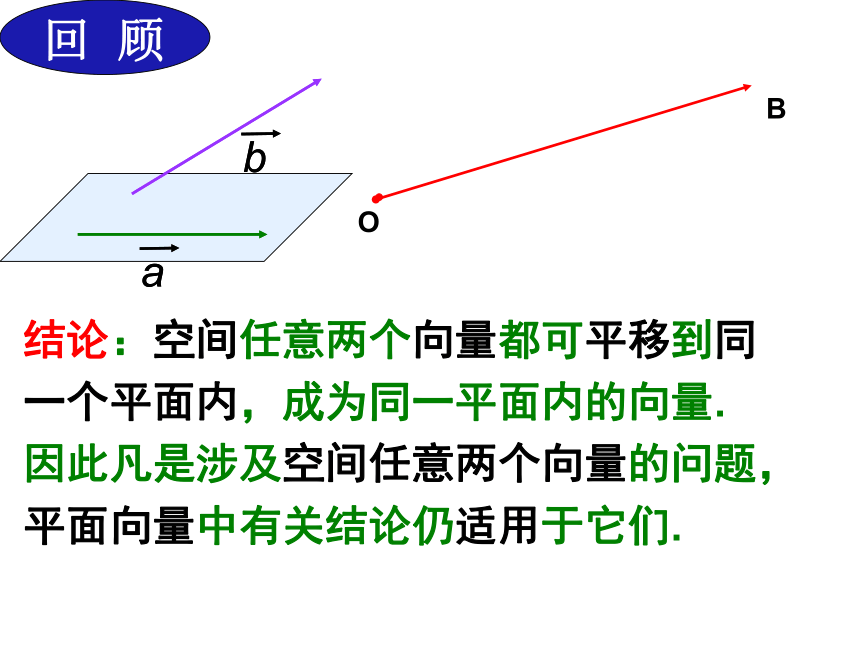
回 顾
a
O
B
b
结论:空间任意两个向量都可平移到同一个平面内,成为同一平面内的向量.
因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们.
b
a
一、空间向量数乘运算
1.实数 与空间向量 的乘积 仍然是一个向量.
当 时,
当 时,
与向量 方向相同;
与向量 方向相同;
是零向量.
当 时,
(1)方向:
(2)大小:
的长度是 的长度的 倍.
2.空间向量的数乘运算满足分配律及结合律
问题2:平面向量中,
的充要条件是:存在唯一
的实数 ,使
能否推广到空间向量中呢?
问题1:若
则
所在直线有那些位置关系
零向量与任意向量共线.
二、共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量),记作
由此可判断空间中两直线平行或三点共线问题
共线向量定理: 对空间任意两个向量 , ,
的充要条件是存在唯一实数λ,
使
性质
判定
如图,l 为经过已知点A且平行已知非零向量 的直线,
a
对空间任意一点O,
所以
即
若在l上取 则有
①和②都称为空间直线的向量表示式,空间任意直线由空间一点及直线的方向向量唯一决定.
由此可判断空间任意三点共线。.
a
l
A
B
P
O
若点P是直线l上任意一点,则
由 知存在唯一的t, 满足
①
②
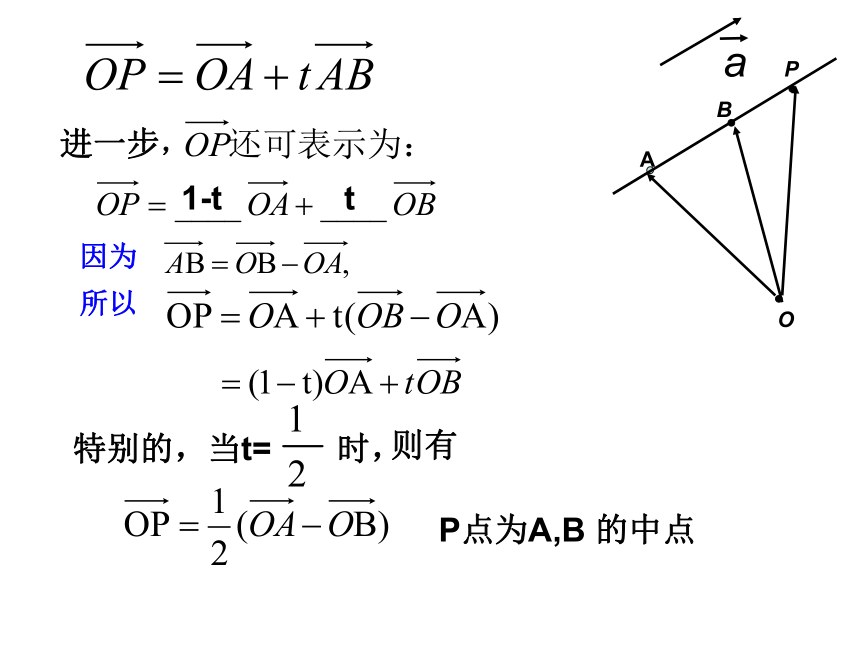
因为
所以
特别的,当t= 时,
则有
a
A
B
P
O
进一步,
t
1-t
P点为A,B 的中点
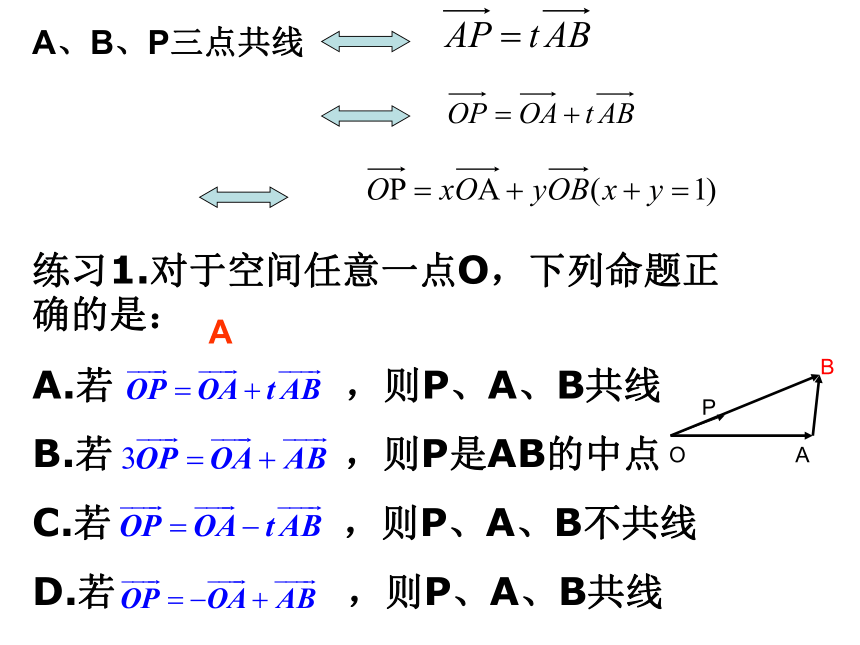
练习1.对于空间任意一点O,下列命题正确的是:
A.若 ,则P、A、B共线
B.若 ,则P是AB的中点
C.若 ,则P、A、B不共线
D.若 ,则P、A、B共线
A、B、P三点共线
A
O
A
B
P
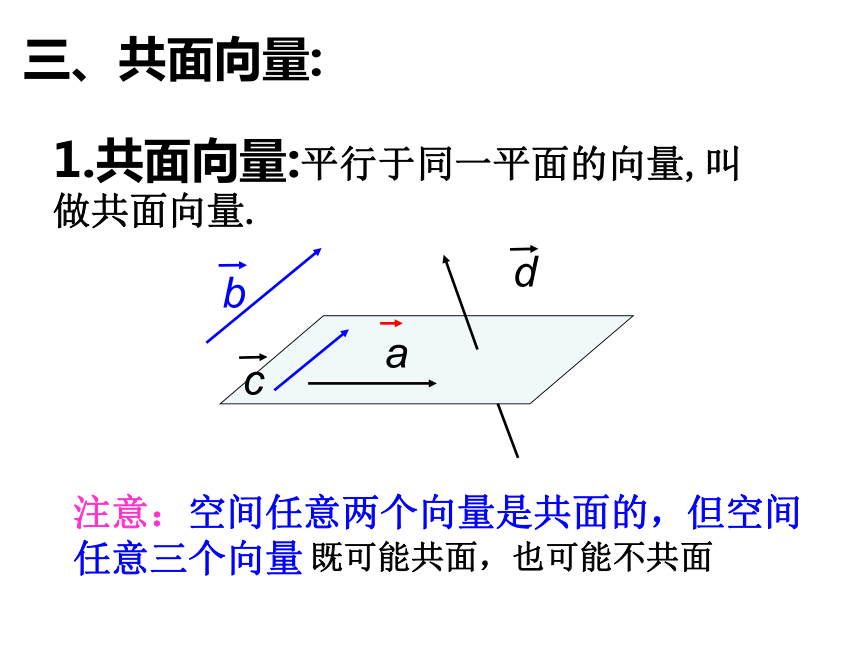
三、共面向量:
1.共面向量:平行于同一平面的向量,叫做共面向量.
注意:空间任意两个向量是共面的,但空间任意三个向量
既可能共面,也可能不共面
d
b
a
c
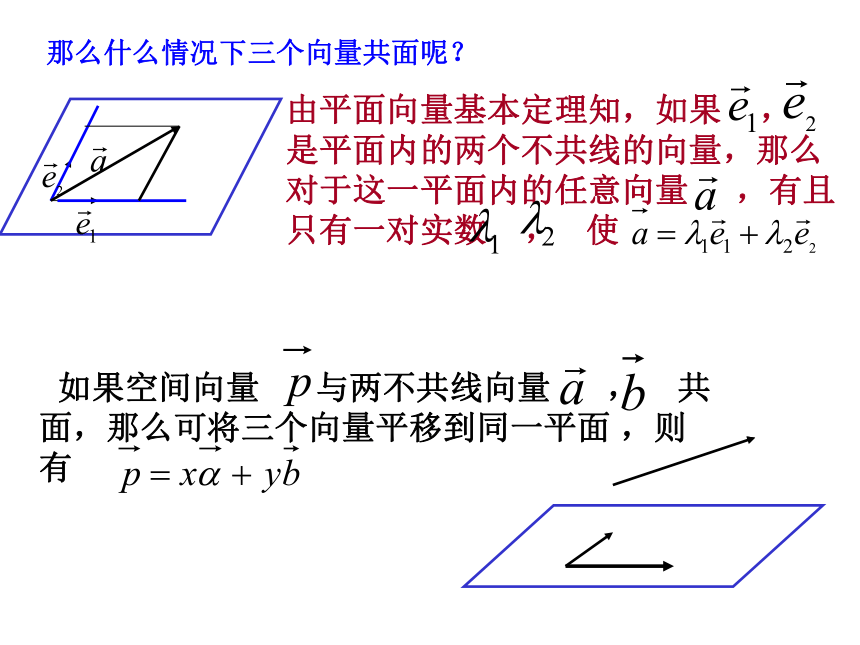
由平面向量基本定理知,如果 ,
是平面内的两个不共线的向量,那么
对于这一平面内的任意向量 ,有且只有一对实数 , 使
如果空间向量 与两不共线向量 , 共
面,那么可将三个向量平移到同一平面 ,则
有
那么什么情况下三个向量共面呢?
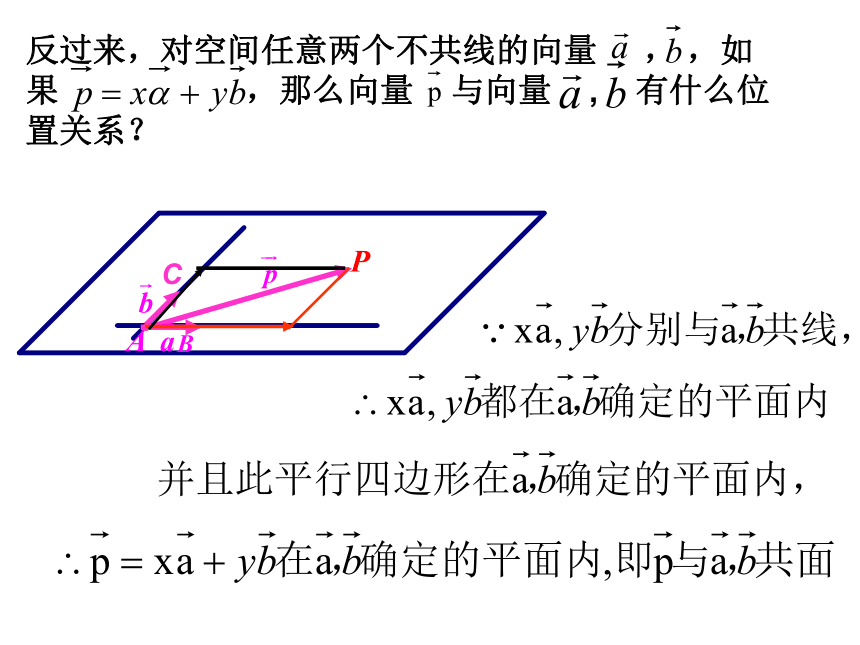
反过来,对空间任意两个不共线的向量 , ,如果 ,那么向量 与向量 , 有什么位
置关系?
C
2.共面向量定理:如果两个向量 , 不共线,
则向量 与向量 , 共面的充要条件是
存在实数对x,y使
推论:空间一点P位于平面ABC内的充要条件是存在有
序实数对x,y使
C
对空间任一点O,有
填空:
1-x-y
x
y
C
③
式称为空间平面ABC的向量表示式,空间中任意平面由空 间一点及两个不共线的向量唯一确定.
③
由此可判断空间任意四点共面
练习2.若对任一点O和不共线的三点A、B、C,
且有
则x+y+z=1
是四点P、A、B、C共面的( )
A.必要不充分条件
C.充要条件
B.充分不必要条件
D.既不充分也不必要条件
C
P与A,B,C共面
解析:由共面向量定理知,要证明P、A、B、C四点共面,只要证明存在有序实数对(x,y)使得
例1. 已知A、B、C三点不共线,对于平面ABC外的任一点O,确定在下列各条件下,点P是否与A、B、C一定共面?
例2. 如图,已知平行四边形ABCD,过平
面AC外一点O作射线OA、OB、OC、OD,在四条射线上分别取点E、F、G、H,并且使
求证:
⑴四点E、F、G、H共面;
⑵平面EG//平面AC.
O
B
A
H
G
F
E
C
D
共线向量 共面向量
定义 向量所在直线互相平行或重合 平行于同一平面的向量,叫做共面向量.
定理
推论
运用 判断三点共线,或两直线平行 判断四点共线,或直线平行于平面
小结
共面
作业:课本89页第2题
W= |F| |s| cos
根据功的计算,我们定义了平面两向量的数量积运算.一旦定义出来,我们发现这种运算非常有用,它能解决有关长度和角度问题.
回 顾
1)两个向量的夹角的定义:
O
A
B
知 新
类似地,可以定义空间向量的
数量积
两个向量的夹角是惟一确定的!
2)两个向量的数量积
注:①两个向量的数量积是数量,而不是向量;
②规定:零向量与任意向量的数量积等于零.
A1
B1
B
A
A1
B1
B
A
数量积 等于 的长度 与 在
的方向上的投影 的乘积.
3)空间两个向量的数量积性质
注:
性质② 是证明两向量垂直的依据;
性质③是求向量的长度(模)的依据.
(4)空间向量的数量积满足的运算律
.
解:
3.
另外,空间向量的运用还经常用来判定空间垂直关系,证两直线垂直线常可转化为证明以这两条线段对应的向量的数量积为零.
证明:
如图,已知:
求证:
在直线l上取向量 ,只要证
为
逆命题成立吗
分析:同样可用向量,证明思路几乎一样,只不过其中的加法运算用减法运算来分析.
分析:要证明一条直线与一个平面
垂直,由直线与平面垂直的定义可知,就是要证明这条直线与平面内的任意一条直线都垂直.
例3(试用向量方法证明直线与平面垂直的判定定理)
已知直线m ,n是平面 内的两条相交直线,
如果 ⊥m, ⊥n,求证: ⊥ .
m
n
g
取已知平面内的任一条直线 g ,拿相关直线的方向向量来分析,看条件可以转化为向量的什么条件 要证的目标可以转化为向量的什么目标 怎样建立向量的条件与向量的目标的联系
共面向量定理,有了!
m
n
g
证:
在 内作不与m ,n重合的任一直线g,在
上取非零向量 因m与n相交,故向量m ,n
不平行,由共面向量定理,存在唯一实数 ,使
通过学习,体会到我们可以利用向量数量积解决立体几何中的以下问题:
1.证明两直线垂直;
2.求两点之间的距离或线段长度;
3.证明线面垂直;
4.求两直线所成角的余弦值等等.
3.1.4空间向量的正交分
解及其坐标表示
共线向量定理:
复习:
共面向量定理:
平面向量基本定理:
平面向量的正交分解及坐标表示
x
y
o
问题:
我们知道,平面内的任意一个向量 都可以用两个不共线的向量 来表示(平面向量基本定理).对于空间任意一个向量,有没有类似的结论呢?
x
y
z
O
Q
P
一、空间向量的坐标分解
给定一个空间坐标系和向量 且设 为空间两两垂直的向量,设点Q为点P在 所确定平面上的正投影
由平面向量基本定理有
一、空间向量的坐标分解
x
y
z
Q
P
O
由此可知,如果 是空间两两垂直的向量,那么,对空间任一向量 , 存在一个有序实数组 {x,y,z}使得
我们称 为向量 在 上的分向量.
空间向量基本定理:
都叫做基向 量
注:
如果三个向量 不共面,那么对空间任一向量 ,存在有序实数组{x,y,z}使
探究:在空间中,如果用任意三个不共面向量
代替两两垂直的向量 ,你能得出类似的
结论吗?
(1)任意不共面的三个向量都可做为空间的一个基底.
特别提示:对于基底{a,b,c},除了应知道a,b,c不共面,
还应明确:
(2 由于可视 为与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是 .
(3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关连的不同概念.
推论:设O、A、B、C是不共线的四点,则对空间任一点P,都存在唯一的有序实数组{x,y,z},使
当且仅当x+y+z=1时,P、A、B、C四点共面。
二、空间直角坐标系
单位正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底,常用e1 , e2 , e3 表示
空间直角坐标系:在空间选定一点O和一个单位正交基底 e1,e2,e3 ,以点O为原点,分别以e1,e2,e3的方向为x轴、y轴、z轴的正方向,建立一个空间直角坐标系O--xyz
x
y
z
e1
e2
e3
O
在空间直角坐标系O--xyz中,对空间任一向量 ,平移使其起点与原点o重合,得到向量OP=P由空间向量基本定理可知,存在有序实数组{x,y,z}使 P =xe1+ye2+ze3
此时向量P的坐标恰是点P在直角坐标系oxyz中的坐标(x,y,z),其中x叫做点P的横坐标,y叫做点P的纵坐标,z叫做点P的竖坐标.
x
y
z
O
P(x,y,z)
e1
e2
e3
在空间直角坐标系O – x y z 中,对空间任一点P, 对应一个向量 ,于是存在唯一的有序实数组 x, y, z,使 (如图).
显然, 向量 的坐标,就是点P在此空间直角坐标系中的坐标(x,y,z).
x
y
z
O
P(x,y,z)
也就是说,以O为起点的有向线段 (向量)的坐标可以和终点的坐标建立起一一对应的关系,从而互相转化.
我们说,点P的坐标为(x,y,z),记作P(x,y,z),其中x叫做点P的横坐标,y叫做点P的纵坐标,z叫做点P的竖坐标.
e1
e2
e3
例题讲解
*
答案
练习2
*
2、已知向量{a,b,c}是空间的一个基底.
求证:向量a+b,a-b,c能构成空间的一个基底.
练习
练习3
3.1.5空间向量运算的坐标表示
z
单位正交基底,空间直角坐标系,向量的坐标
x
y
O
(x,y,z)
P
Q
启示:空间向量OP = (x,y,z)
OP
=
OQ
+
QP
=
复习
则
1.复习平面向量的坐标运算(1)
设
设M=(x,y),若M是线段AB的中点,
类比平面向量,空间向量的坐标运算是怎样的呢
则
类比可得空间向量的坐标运算(1)
设
设M=(x,y,z),若M是线段AB的中点,
2.平面向量的数量积、距离与夹角
1.距离公式
2.夹角公式
类比可得空间向量的数量积、距离与夹角
1.距离公式
2.夹角公式
数量积运算的证明:
所以
利用向量数量积的分配律及
得到:
解:
应用
( )
1.已知
(1)
(4)
(2)
(3)
例2 如图,在正方体 中,
,求 与 所成的角的余弦值。
解:设正方体的棱长为1,如图建
立空间直角坐标系 ,则
例2 如图,在正方体 中,
,求 与 所成的角的余弦值。
O
例3.如图,在正方体 中,E,F分别是
的中点,求证
证明:不妨设已知正方体的棱长为1个单
位长度,设
分别以 为坐标向量建立空间直
角坐标系 则
x
z
1.若E1,F1分别是A'B'和C'D'
的一个四等分点,那么
又是多少呢?
(1,1,0)
y
F1
o
A
D
B
B '
C '
C
A '
D '
E1
(0,0,0)
答案:
2.已知a=(1,0),b=(m,m)(m>0),则〈a,b〉=________
45°
证明:不妨设已知正方体的棱长为1个单
位长度,设
分别以 为坐标向量建立空间直
角坐标系 则
(1)熟练掌握空间向量坐标表示的各种运算律;
确定空间几何体中顶点和向量的坐标.
(2)空间向量中的公式的形式与平面向量中相
关内容一致,因此可类比记忆.
1、重点:
2、难点:
山东省临沂第二中学
———共线向量与共面向量
回 顾
a
O
B
b
结论:空间任意两个向量都可平移到同一个平面内,成为同一平面内的向量.
因此凡是涉及空间任意两个向量的问题,平面向量中有关结论仍适用于它们.
b
a
一、空间向量数乘运算
1.实数 与空间向量 的乘积 仍然是一个向量.
当 时,
当 时,
与向量 方向相同;
与向量 方向相同;
是零向量.
当 时,
(1)方向:
(2)大小:
的长度是 的长度的 倍.
2.空间向量的数乘运算满足分配律及结合律
问题2:平面向量中,
的充要条件是:存在唯一
的实数 ,使
能否推广到空间向量中呢?
问题1:若
则
所在直线有那些位置关系
零向量与任意向量共线.
二、共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量),记作
由此可判断空间中两直线平行或三点共线问题
共线向量定理: 对空间任意两个向量 , ,
的充要条件是存在唯一实数λ,
使
性质
判定
如图,l 为经过已知点A且平行已知非零向量 的直线,
a
对空间任意一点O,
所以
即
若在l上取 则有
①和②都称为空间直线的向量表示式,空间任意直线由空间一点及直线的方向向量唯一决定.
由此可判断空间任意三点共线。.
a
l
A
B
P
O
若点P是直线l上任意一点,则
由 知存在唯一的t, 满足
①
②
因为
所以
特别的,当t= 时,
则有
a
A
B
P
O
进一步,
t
1-t
P点为A,B 的中点
练习1.对于空间任意一点O,下列命题正确的是:
A.若 ,则P、A、B共线
B.若 ,则P是AB的中点
C.若 ,则P、A、B不共线
D.若 ,则P、A、B共线
A、B、P三点共线
A
O
A
B
P
三、共面向量:
1.共面向量:平行于同一平面的向量,叫做共面向量.
注意:空间任意两个向量是共面的,但空间任意三个向量
既可能共面,也可能不共面
d
b
a
c
由平面向量基本定理知,如果 ,
是平面内的两个不共线的向量,那么
对于这一平面内的任意向量 ,有且只有一对实数 , 使
如果空间向量 与两不共线向量 , 共
面,那么可将三个向量平移到同一平面 ,则
有
那么什么情况下三个向量共面呢?
反过来,对空间任意两个不共线的向量 , ,如果 ,那么向量 与向量 , 有什么位
置关系?
C
2.共面向量定理:如果两个向量 , 不共线,
则向量 与向量 , 共面的充要条件是
存在实数对x,y使
推论:空间一点P位于平面ABC内的充要条件是存在有
序实数对x,y使
C
对空间任一点O,有
填空:
1-x-y
x
y
C
③
式称为空间平面ABC的向量表示式,空间中任意平面由空 间一点及两个不共线的向量唯一确定.
③
由此可判断空间任意四点共面
练习2.若对任一点O和不共线的三点A、B、C,
且有
则x+y+z=1
是四点P、A、B、C共面的( )
A.必要不充分条件
C.充要条件
B.充分不必要条件
D.既不充分也不必要条件
C
P与A,B,C共面
解析:由共面向量定理知,要证明P、A、B、C四点共面,只要证明存在有序实数对(x,y)使得
例1. 已知A、B、C三点不共线,对于平面ABC外的任一点O,确定在下列各条件下,点P是否与A、B、C一定共面?
例2. 如图,已知平行四边形ABCD,过平
面AC外一点O作射线OA、OB、OC、OD,在四条射线上分别取点E、F、G、H,并且使
求证:
⑴四点E、F、G、H共面;
⑵平面EG//平面AC.
O
B
A
H
G
F
E
C
D
共线向量 共面向量
定义 向量所在直线互相平行或重合 平行于同一平面的向量,叫做共面向量.
定理
推论
运用 判断三点共线,或两直线平行 判断四点共线,或直线平行于平面
小结
共面
作业:课本89页第2题
W= |F| |s| cos
根据功的计算,我们定义了平面两向量的数量积运算.一旦定义出来,我们发现这种运算非常有用,它能解决有关长度和角度问题.
回 顾
1)两个向量的夹角的定义:
O
A
B
知 新
类似地,可以定义空间向量的
数量积
两个向量的夹角是惟一确定的!
2)两个向量的数量积
注:①两个向量的数量积是数量,而不是向量;
②规定:零向量与任意向量的数量积等于零.
A1
B1
B
A
A1
B1
B
A
数量积 等于 的长度 与 在
的方向上的投影 的乘积.
3)空间两个向量的数量积性质
注:
性质② 是证明两向量垂直的依据;
性质③是求向量的长度(模)的依据.
(4)空间向量的数量积满足的运算律
.
解:
3.
另外,空间向量的运用还经常用来判定空间垂直关系,证两直线垂直线常可转化为证明以这两条线段对应的向量的数量积为零.
证明:
如图,已知:
求证:
在直线l上取向量 ,只要证
为
逆命题成立吗
分析:同样可用向量,证明思路几乎一样,只不过其中的加法运算用减法运算来分析.
分析:要证明一条直线与一个平面
垂直,由直线与平面垂直的定义可知,就是要证明这条直线与平面内的任意一条直线都垂直.
例3(试用向量方法证明直线与平面垂直的判定定理)
已知直线m ,n是平面 内的两条相交直线,
如果 ⊥m, ⊥n,求证: ⊥ .
m
n
g
取已知平面内的任一条直线 g ,拿相关直线的方向向量来分析,看条件可以转化为向量的什么条件 要证的目标可以转化为向量的什么目标 怎样建立向量的条件与向量的目标的联系
共面向量定理,有了!
m
n
g
证:
在 内作不与m ,n重合的任一直线g,在
上取非零向量 因m与n相交,故向量m ,n
不平行,由共面向量定理,存在唯一实数 ,使
通过学习,体会到我们可以利用向量数量积解决立体几何中的以下问题:
1.证明两直线垂直;
2.求两点之间的距离或线段长度;
3.证明线面垂直;
4.求两直线所成角的余弦值等等.
3.1.4空间向量的正交分
解及其坐标表示
共线向量定理:
复习:
共面向量定理:
平面向量基本定理:
平面向量的正交分解及坐标表示
x
y
o
问题:
我们知道,平面内的任意一个向量 都可以用两个不共线的向量 来表示(平面向量基本定理).对于空间任意一个向量,有没有类似的结论呢?
x
y
z
O
Q
P
一、空间向量的坐标分解
给定一个空间坐标系和向量 且设 为空间两两垂直的向量,设点Q为点P在 所确定平面上的正投影
由平面向量基本定理有
一、空间向量的坐标分解
x
y
z
Q
P
O
由此可知,如果 是空间两两垂直的向量,那么,对空间任一向量 , 存在一个有序实数组 {x,y,z}使得
我们称 为向量 在 上的分向量.
空间向量基本定理:
都叫做基向 量
注:
如果三个向量 不共面,那么对空间任一向量 ,存在有序实数组{x,y,z}使
探究:在空间中,如果用任意三个不共面向量
代替两两垂直的向量 ,你能得出类似的
结论吗?
(1)任意不共面的三个向量都可做为空间的一个基底.
特别提示:对于基底{a,b,c},除了应知道a,b,c不共面,
还应明确:
(2 由于可视 为与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是 .
(3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关连的不同概念.
推论:设O、A、B、C是不共线的四点,则对空间任一点P,都存在唯一的有序实数组{x,y,z},使
当且仅当x+y+z=1时,P、A、B、C四点共面。
二、空间直角坐标系
单位正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底,常用e1 , e2 , e3 表示
空间直角坐标系:在空间选定一点O和一个单位正交基底 e1,e2,e3 ,以点O为原点,分别以e1,e2,e3的方向为x轴、y轴、z轴的正方向,建立一个空间直角坐标系O--xyz
x
y
z
e1
e2
e3
O
在空间直角坐标系O--xyz中,对空间任一向量 ,平移使其起点与原点o重合,得到向量OP=P由空间向量基本定理可知,存在有序实数组{x,y,z}使 P =xe1+ye2+ze3
此时向量P的坐标恰是点P在直角坐标系oxyz中的坐标(x,y,z),其中x叫做点P的横坐标,y叫做点P的纵坐标,z叫做点P的竖坐标.
x
y
z
O
P(x,y,z)
e1
e2
e3
在空间直角坐标系O – x y z 中,对空间任一点P, 对应一个向量 ,于是存在唯一的有序实数组 x, y, z,使 (如图).
显然, 向量 的坐标,就是点P在此空间直角坐标系中的坐标(x,y,z).
x
y
z
O
P(x,y,z)
也就是说,以O为起点的有向线段 (向量)的坐标可以和终点的坐标建立起一一对应的关系,从而互相转化.
我们说,点P的坐标为(x,y,z),记作P(x,y,z),其中x叫做点P的横坐标,y叫做点P的纵坐标,z叫做点P的竖坐标.
e1
e2
e3
例题讲解
*
答案
练习2
*
2、已知向量{a,b,c}是空间的一个基底.
求证:向量a+b,a-b,c能构成空间的一个基底.
练习
练习3
3.1.5空间向量运算的坐标表示
z
单位正交基底,空间直角坐标系,向量的坐标
x
y
O
(x,y,z)
P
Q
启示:空间向量OP = (x,y,z)
OP
=
OQ
+
QP
=
复习
则
1.复习平面向量的坐标运算(1)
设
设M=(x,y),若M是线段AB的中点,
类比平面向量,空间向量的坐标运算是怎样的呢
则
类比可得空间向量的坐标运算(1)
设
设M=(x,y,z),若M是线段AB的中点,
2.平面向量的数量积、距离与夹角
1.距离公式
2.夹角公式
类比可得空间向量的数量积、距离与夹角
1.距离公式
2.夹角公式
数量积运算的证明:
所以
利用向量数量积的分配律及
得到:
解:
应用
( )
1.已知
(1)
(4)
(2)
(3)
例2 如图,在正方体 中,
,求 与 所成的角的余弦值。
解:设正方体的棱长为1,如图建
立空间直角坐标系 ,则
例2 如图,在正方体 中,
,求 与 所成的角的余弦值。
O
例3.如图,在正方体 中,E,F分别是
的中点,求证
证明:不妨设已知正方体的棱长为1个单
位长度,设
分别以 为坐标向量建立空间直
角坐标系 则
x
z
1.若E1,F1分别是A'B'和C'D'
的一个四等分点,那么
又是多少呢?
(1,1,0)
y
F1
o
A
D
B
B '
C '
C
A '
D '
E1
(0,0,0)
答案:
2.已知a=(1,0),b=(m,m)(m>0),则〈a,b〉=________
45°
证明:不妨设已知正方体的棱长为1个单
位长度,设
分别以 为坐标向量建立空间直
角坐标系 则
(1)熟练掌握空间向量坐标表示的各种运算律;
确定空间几何体中顶点和向量的坐标.
(2)空间向量中的公式的形式与平面向量中相
关内容一致,因此可类比记忆.
1、重点:
2、难点:
