3.2 空间向量在立体几何中的应用
文档属性
| 名称 | 3.2 空间向量在立体几何中的应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 280.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-05 18:05:22 | ||
图片预览




文档简介
(共20张PPT)
两直线夹角:[0°,90°]
异面直线所成角:(0°,90°] 直线和平面所成的角:[0°,90°]
两向量夹角:[0°,180°]
到角:[0°,180°)
直线的倾斜角:[0°,180°) 二面角:[0°,180°]
-----直线的方向向量与平面的法向量
3.2立体几何中的向量方法(一)
上一节,我们把向量从平面推广到空间,并利用空间向量解决了一些立体几何问题.本节我们进一步学习立体几何中的向量方法.
立体几何研究的基本对象是点、直线、平面以及由它们组成的空间图形.为了用空间向量解决立体几何问题,首先必须把点、直线、平面的位置用向量表示出来.
思考
如何确定一个点在空间的位置 在空间中给一个定点A和一个定方向(向量),能确定一条直线在空间的位置吗 给一个定点和两个定方向(向量),能确定一个平面在空间的位置吗 给一个定点和一个定方向(向量),能确定一个平面在空间的位置吗
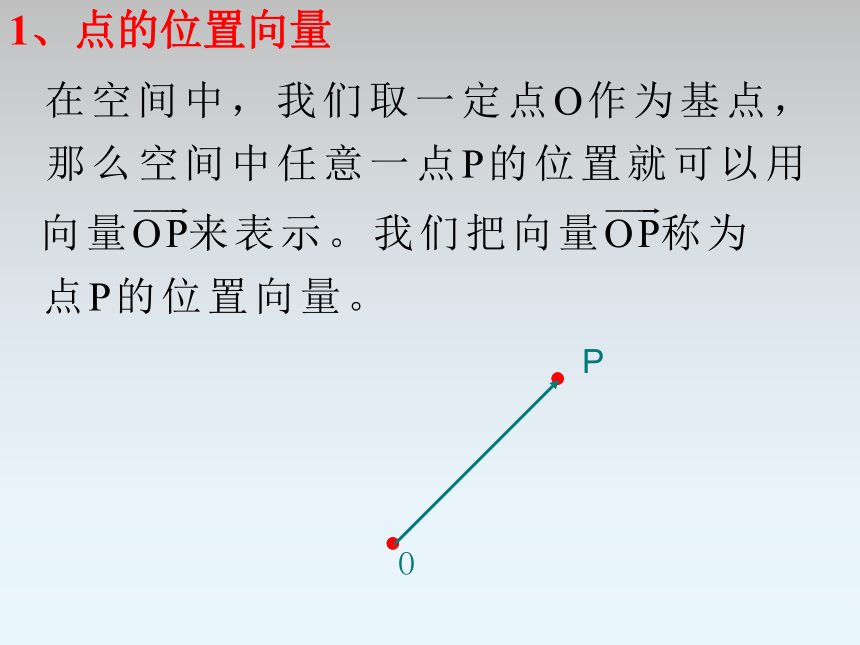
O
P
1、点的位置向量
A
B
P
2、直线的方向向量
这样,点A和向量 不仅可以确定直线l的位置,还可以具体表示出l上的任意一点.
α
o
b
a
P
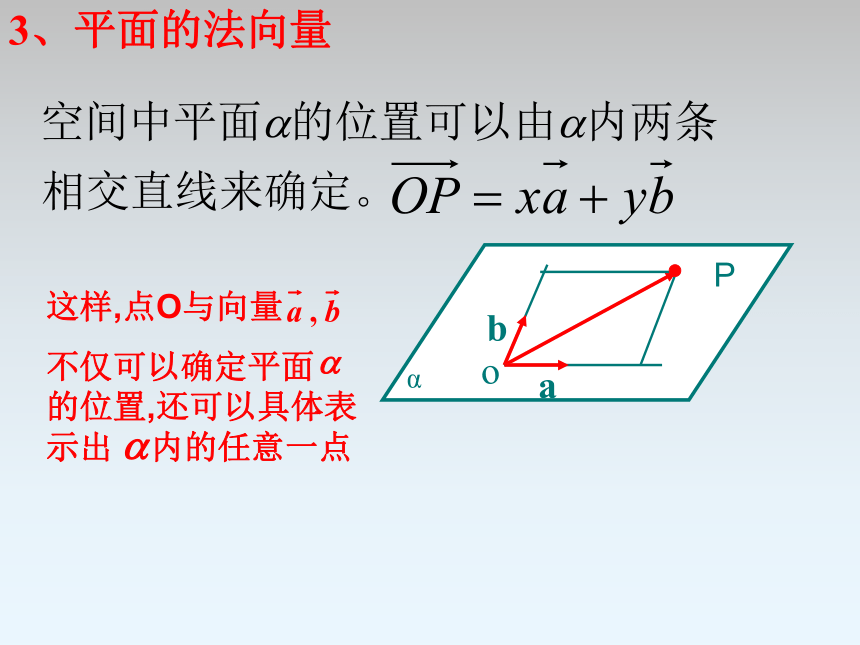
3、平面的法向量
这样,点O与向量
不仅可以确定平面 的位置,还可以具体表示出 内的任意一点
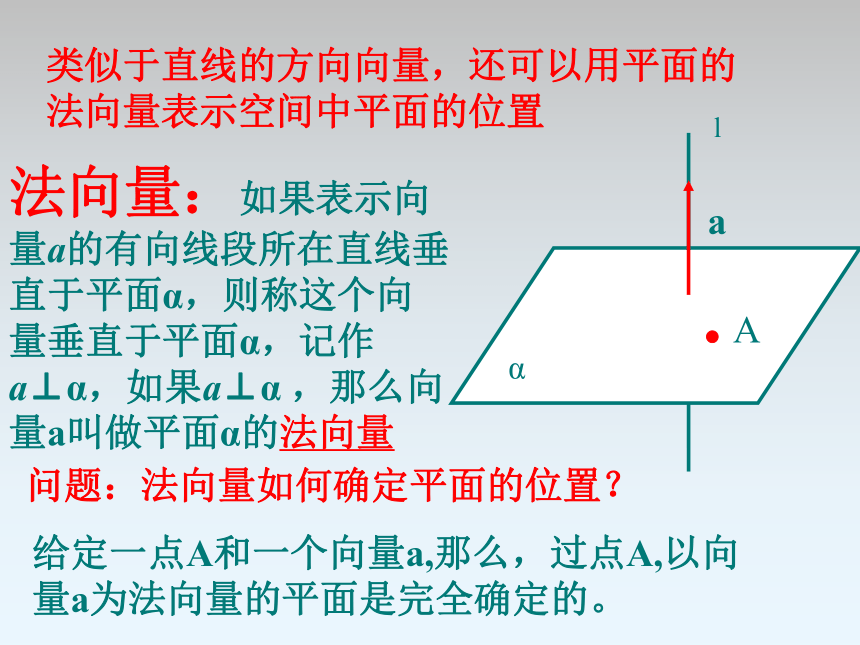
法向量:如果表示向量a的有向线段所在直线垂直于平面α,则称这个向量垂直于平面α,记作a⊥α,如果a⊥α ,那么向量a叫做平面α的法向量
α
l
a
类似于直线的方向向量,还可以用平面的
法向量表示空间中平面的位置
问题:法向量如何确定平面的位置?
A
给定一点A和一个向量a,那么,过点A,以向量a为法向量的平面是完全确定的。
因为方向向量与法向量可以确定直线和平面的位置,所以我们可以利用直线的方向向量与平面的法向量表示空间直线、平面间的平行、垂直、夹角等位置关系。
4、法向量的运用
例1 (1)设 分别是直线 的方向向量,根据下列条件判断 与 的位置关系:
②
③
分析:直线方向向量与直线位置关系,
据此可判断两直线的位置关系
①平行②垂直③相交或异面
例1 (2)设 分别是平面 的法向量,根据下列条件判断 与 的位置关系:
②
③
分析:平面法向量与两平面位置关系,
据此可判断两平面的位置关系
①垂直②平行③相交(不垂直)
分析:直线方向向量与平面法向量关系和直线与平面位置关系,
据此可判断直线和平面的位置关系
例1 (3)设 是平面 的法向量, 是直线 的方向向量,根据下列条件判断 与 的位置关系:
②
③
① ②垂直③相交(斜交)
例2 已知平面 经过三点A(1,2,3) 、B(2,0,-1) 、C(3,-2,0),试求平面 的一个法向量.
解:∵ A(1,2,3) 、B(2,0,-1) 、C(3,-2,0)
∴
设平面 的法向量是
依题意,有 ,即
解得z=0且x=2y,令y=1,则x=2
∴平面 的一个法向量是
例3 一条直线与一个平面内两条相交直线都垂直,则该直线与此平面垂直.
已知:直线m,n是平面 内的任意两条相交直线,且l⊥m,l ⊥n.求证:l ⊥
证明:设直线l,m,n的方向向量分别为
因为l⊥m,l ⊥n,所以 同理
因为m,n ,且m,n相交,
所以 内任一直线的方向向量 可以表示为
因为
所以 与 内任一直线垂直. 因此
小结
1.直线的方向向量和平面的法向量是用空间向量解决立体几何问题的两个重要工具,是实现空间问题的向量方法的媒介.
2.要熟练掌握用直线的方向向量和平面的法向量来研究直线、平面之间关系的原理与方法,特别是直线、平面的位置关系与方向向量、法向量之间的联系.
P104 练习 1 2
P111 习题3.2 2
作业
两直线夹角:[0°,90°]
异面直线所成角:(0°,90°] 直线和平面所成的角:[0°,90°]
两向量夹角:[0°,180°]
到角:[0°,180°)
直线的倾斜角:[0°,180°) 二面角:[0°,180°]
-----直线的方向向量与平面的法向量
3.2立体几何中的向量方法(一)
上一节,我们把向量从平面推广到空间,并利用空间向量解决了一些立体几何问题.本节我们进一步学习立体几何中的向量方法.
立体几何研究的基本对象是点、直线、平面以及由它们组成的空间图形.为了用空间向量解决立体几何问题,首先必须把点、直线、平面的位置用向量表示出来.
思考
如何确定一个点在空间的位置 在空间中给一个定点A和一个定方向(向量),能确定一条直线在空间的位置吗 给一个定点和两个定方向(向量),能确定一个平面在空间的位置吗 给一个定点和一个定方向(向量),能确定一个平面在空间的位置吗
O
P
1、点的位置向量
A
B
P
2、直线的方向向量
这样,点A和向量 不仅可以确定直线l的位置,还可以具体表示出l上的任意一点.
α
o
b
a
P
3、平面的法向量
这样,点O与向量
不仅可以确定平面 的位置,还可以具体表示出 内的任意一点
法向量:如果表示向量a的有向线段所在直线垂直于平面α,则称这个向量垂直于平面α,记作a⊥α,如果a⊥α ,那么向量a叫做平面α的法向量
α
l
a
类似于直线的方向向量,还可以用平面的
法向量表示空间中平面的位置
问题:法向量如何确定平面的位置?
A
给定一点A和一个向量a,那么,过点A,以向量a为法向量的平面是完全确定的。
因为方向向量与法向量可以确定直线和平面的位置,所以我们可以利用直线的方向向量与平面的法向量表示空间直线、平面间的平行、垂直、夹角等位置关系。
4、法向量的运用
例1 (1)设 分别是直线 的方向向量,根据下列条件判断 与 的位置关系:
②
③
分析:直线方向向量与直线位置关系,
据此可判断两直线的位置关系
①平行②垂直③相交或异面
例1 (2)设 分别是平面 的法向量,根据下列条件判断 与 的位置关系:
②
③
分析:平面法向量与两平面位置关系,
据此可判断两平面的位置关系
①垂直②平行③相交(不垂直)
分析:直线方向向量与平面法向量关系和直线与平面位置关系,
据此可判断直线和平面的位置关系
例1 (3)设 是平面 的法向量, 是直线 的方向向量,根据下列条件判断 与 的位置关系:
②
③
① ②垂直③相交(斜交)
例2 已知平面 经过三点A(1,2,3) 、B(2,0,-1) 、C(3,-2,0),试求平面 的一个法向量.
解:∵ A(1,2,3) 、B(2,0,-1) 、C(3,-2,0)
∴
设平面 的法向量是
依题意,有 ,即
解得z=0且x=2y,令y=1,则x=2
∴平面 的一个法向量是
例3 一条直线与一个平面内两条相交直线都垂直,则该直线与此平面垂直.
已知:直线m,n是平面 内的任意两条相交直线,且l⊥m,l ⊥n.求证:l ⊥
证明:设直线l,m,n的方向向量分别为
因为l⊥m,l ⊥n,所以 同理
因为m,n ,且m,n相交,
所以 内任一直线的方向向量 可以表示为
因为
所以 与 内任一直线垂直. 因此
小结
1.直线的方向向量和平面的法向量是用空间向量解决立体几何问题的两个重要工具,是实现空间问题的向量方法的媒介.
2.要熟练掌握用直线的方向向量和平面的法向量来研究直线、平面之间关系的原理与方法,特别是直线、平面的位置关系与方向向量、法向量之间的联系.
P104 练习 1 2
P111 习题3.2 2
作业
