3.1.1 两角和与差的余弦
图片预览








文档简介
(共22张PPT)
问题提出
若已知α,β的三角函数值,那么cos(α-β)的值是否确定?它与α,β的三角函数值有什么关系?这是我们需要探索的问题.
海南省洋浦中学:赵生碧
探究(一):两角差的余弦公式
思考1:设α,β为两个任意角, 你能判断cos(α-β)=cosα-cosβ恒成立吗
cos(45°-30°)≠cos45°-cos30°
sin60°
sin120°
cos60°
cos120°
cos(120°-60°)
sin30°
sin60°
cos30°
cos60°
cos(60°-30°)
思考2:我们设想cos(α-β)的值与α,β的三角函数值有一定关系,观察下表中的数据,你有什么发现?
思考3:一般地,你猜想cos(α-β)等于什么?
cos(α-β)=cosαcosβ+sinαsinβ
思考4:如图,设α,β为锐角,且α>β,角α的终边与单位圆的交点为P1, ∠P1OP=β,那么cos(α-β)表示哪条线段长?
M
P
P1
O
x
y
cos(α-β)=OM
思考5:如何用线段分别表示sinβ和cosβ?
P
P1
O
x
y
A
sinβ
cosβ
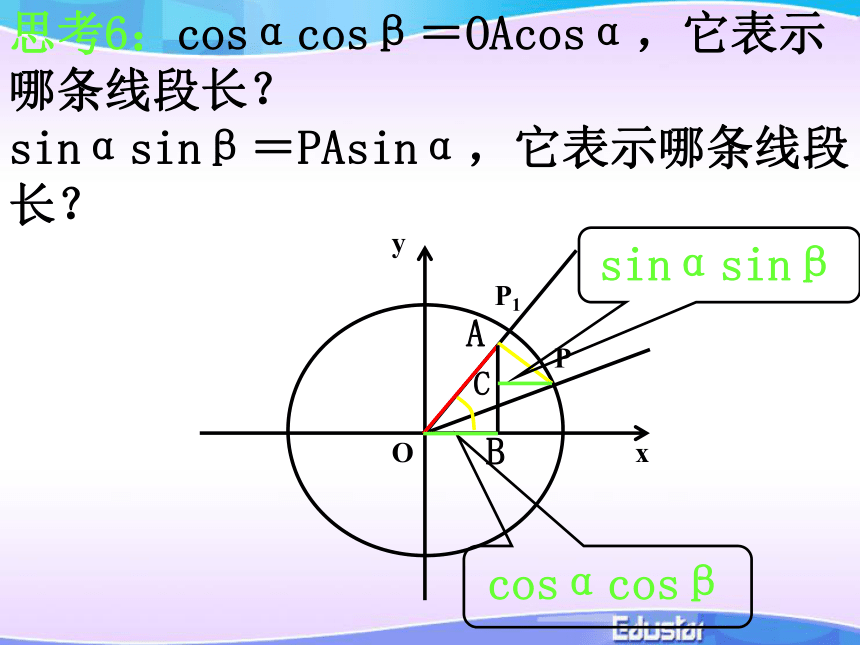
思考6:cosαcosβ=OAcosα,它表示哪条线段长?
sinαsinβ=PAsinα,它表示哪条线段长?
P
P1
O
x
y
A
sinαsinβ
cosαcosβ
B
C
思考7:利用OM=OB+BM=OB+CP可得什么结论?
sinαsinβ
cosαcosβ
P
P1
O
x
y
A
B
C
M
cos(α-β)=cosαcosβ+sinαsinβ
x
y
P
P1
M
B
O
A
C
+
1
1
思考8:上述推理能说明对任意角α,β,都有
cos(α-β)=cosαcosβ+sinαsinβ成立吗?
思考9:根据cosαcosβ+sinαsinβ的结构特征,你能联想到一个相关计算原理吗?
思考10:如图,设角α,β的终边与单位圆的交点分别为A、B,则向量 、
的坐标分别是什么?其数量积是什么?
B
O
A
x
y
α
β
=(cosα,sinα)
=(cosβ,sinβ)
思考11:向量与的夹角θ与α、β有什么关系?根据数量积定义, 等于什么?由此可得什么结论?
α=2kπ+β+θ或β=2kπ+α+θ
B
O
A
x
y
α
β
θ
cos(α-β)=cosαcosβ+sinαsinβ
思考12:公式cos(α-β)=cosαcosβ+sinαsinβ称为差角的余弦公式,记作 ,该公式有什么特点?如何记忆?
例1 利用余弦公式求cos15°的值.
例2 已知
β是第三象限角,求cos(α-β)的值.
理论迁移
【理论迁移、巩固深化】
1. = .
2. = .
3.已知 ,
求 的值.
【巩固深化,发展思维】
已知 ,
是第三象限角,求 的值.
小结作业
1、两角差的余弦公式,首先要认识公式结构的特征,了解公式的推导过程,熟知由此衍变的两角和的余弦公式.在解题过程中注意角 、 的象限,也就是符号问题,学会灵活运用.
2、牢记公式
3.在差角的余弦公式中,α,β既可以是单角,也可以是复角,运用时要注意角的变换,如,2β=(α+β)-(α-β) 等. 同时,公式的应用具有灵活性,解题时要注意正向、逆向和变式形式的选择.
1、不查表计算下列各值
①
②
2.已知 且 ;
求 的值。
作 业
问题提出
若已知α,β的三角函数值,那么cos(α-β)的值是否确定?它与α,β的三角函数值有什么关系?这是我们需要探索的问题.
海南省洋浦中学:赵生碧
探究(一):两角差的余弦公式
思考1:设α,β为两个任意角, 你能判断cos(α-β)=cosα-cosβ恒成立吗
cos(45°-30°)≠cos45°-cos30°
sin60°
sin120°
cos60°
cos120°
cos(120°-60°)
sin30°
sin60°
cos30°
cos60°
cos(60°-30°)
思考2:我们设想cos(α-β)的值与α,β的三角函数值有一定关系,观察下表中的数据,你有什么发现?
思考3:一般地,你猜想cos(α-β)等于什么?
cos(α-β)=cosαcosβ+sinαsinβ
思考4:如图,设α,β为锐角,且α>β,角α的终边与单位圆的交点为P1, ∠P1OP=β,那么cos(α-β)表示哪条线段长?
M
P
P1
O
x
y
cos(α-β)=OM
思考5:如何用线段分别表示sinβ和cosβ?
P
P1
O
x
y
A
sinβ
cosβ
思考6:cosαcosβ=OAcosα,它表示哪条线段长?
sinαsinβ=PAsinα,它表示哪条线段长?
P
P1
O
x
y
A
sinαsinβ
cosαcosβ
B
C
思考7:利用OM=OB+BM=OB+CP可得什么结论?
sinαsinβ
cosαcosβ
P
P1
O
x
y
A
B
C
M
cos(α-β)=cosαcosβ+sinαsinβ
x
y
P
P1
M
B
O
A
C
+
1
1
思考8:上述推理能说明对任意角α,β,都有
cos(α-β)=cosαcosβ+sinαsinβ成立吗?
思考9:根据cosαcosβ+sinαsinβ的结构特征,你能联想到一个相关计算原理吗?
思考10:如图,设角α,β的终边与单位圆的交点分别为A、B,则向量 、
的坐标分别是什么?其数量积是什么?
B
O
A
x
y
α
β
=(cosα,sinα)
=(cosβ,sinβ)
思考11:向量与的夹角θ与α、β有什么关系?根据数量积定义, 等于什么?由此可得什么结论?
α=2kπ+β+θ或β=2kπ+α+θ
B
O
A
x
y
α
β
θ
cos(α-β)=cosαcosβ+sinαsinβ
思考12:公式cos(α-β)=cosαcosβ+sinαsinβ称为差角的余弦公式,记作 ,该公式有什么特点?如何记忆?
例1 利用余弦公式求cos15°的值.
例2 已知
β是第三象限角,求cos(α-β)的值.
理论迁移
【理论迁移、巩固深化】
1. = .
2. = .
3.已知 ,
求 的值.
【巩固深化,发展思维】
已知 ,
是第三象限角,求 的值.
小结作业
1、两角差的余弦公式,首先要认识公式结构的特征,了解公式的推导过程,熟知由此衍变的两角和的余弦公式.在解题过程中注意角 、 的象限,也就是符号问题,学会灵活运用.
2、牢记公式
3.在差角的余弦公式中,α,β既可以是单角,也可以是复角,运用时要注意角的变换,如,2β=(α+β)-(α-β) 等. 同时,公式的应用具有灵活性,解题时要注意正向、逆向和变式形式的选择.
1、不查表计算下列各值
①
②
2.已知 且 ;
求 的值。
作 业
