1.1.2 弧度制和弧度制与角度制的换算
文档属性
| 名称 | 1.1.2 弧度制和弧度制与角度制的换算 |

|
|
| 格式 | zip | ||
| 文件大小 | 166.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-05 18:05:22 | ||
图片预览




文档简介
(共14张PPT)
1、角的度量
角度制
角可以用度为单位进行度量,1度的角等于周角的1/360。这种用度作为单位来度量角的单位制叫做角度制。
在角度制下,当把两个带着度、分、秒
单位的角相加、相减时,运算进率是什么进
制的?那么我们能否重新选择角单位?
思考:
弧度制
我们把长度等于半径长的弧所对的圆心角叫做1弧度的角,用符号rad表示,读作弧度。这种用弧度作为单位度量角的单位制叫做弧度制。
若弧是一个半圆,则其圆心角的弧度数是多少?若弧是一个整圆呢?
r
r
弧度制
注:
“弧度”不是弧长,它是一个比值。值有正负。
一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0,如果半径为r的圆的圆心角a所对弧的长为l,那么,角a的弧度数的绝对值是 | a | = l / r
a的正负由角a的终边的旋转方向决定。
r
l
a
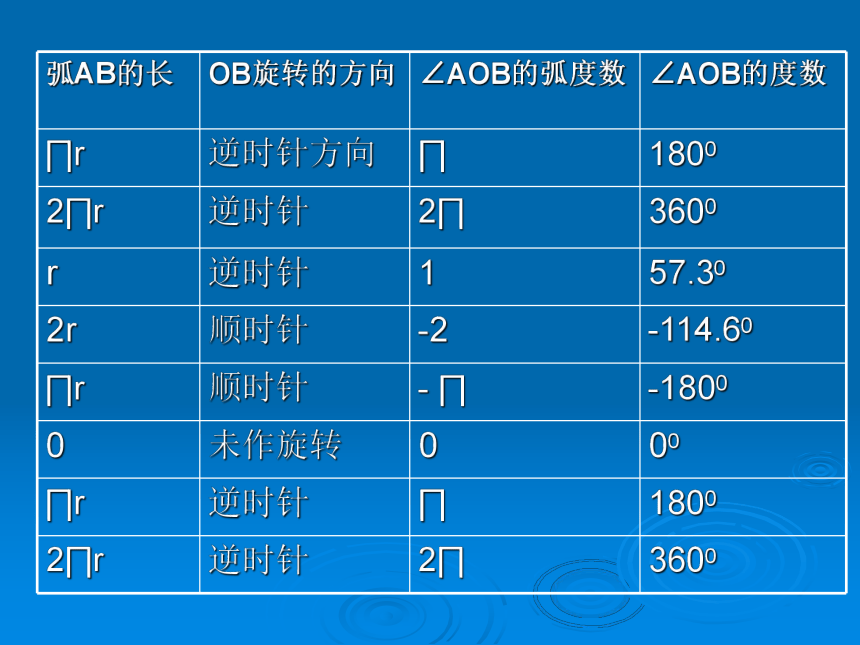
完成课本P7 探究
弧AB的长 OB旋转的方向 ∠AOB的弧度数 ∠AOB的度数
∏r 逆时针方向 ∏ 1800
2∏r 逆时针 2∏ 3600
r 逆时针 1 57.30
2r 顺时针 -2 -114.60
∏r 顺时针 - ∏ -1800
0 未作旋转 0 00
∏r 逆时针 ∏ 1800
2∏r 逆时针 2∏ 3600
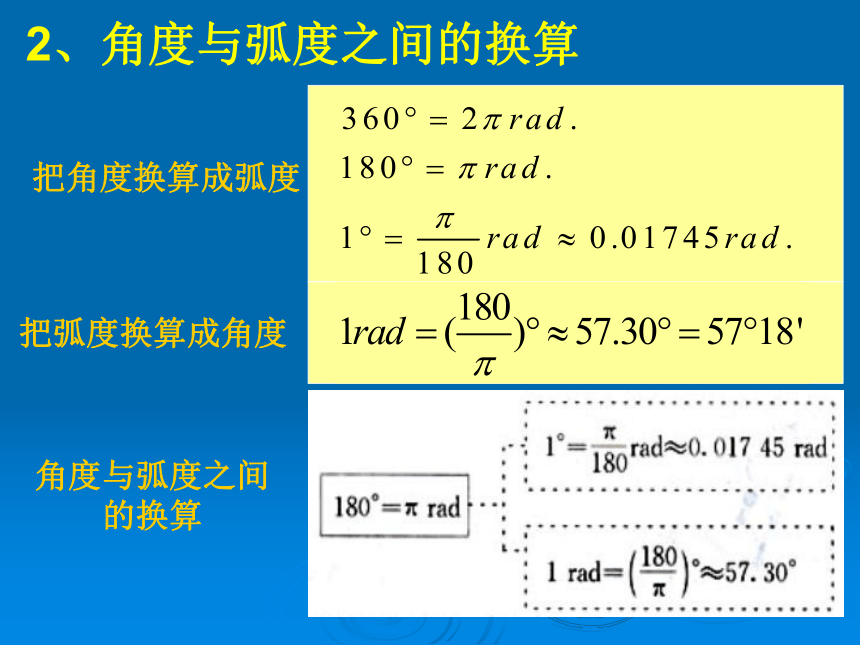
2、角度与弧度之间的换算
把角度换算成弧度
把弧度换算成角度
角度与弧度之间的换算
填写下列特殊角的度数和弧度数的对应表。
角度
弧度
2、角度与弧度之间的换算
正角
零角
负角
正实数
0
负实数
任意角的集合
实数集R
角的概念推广后,在弧度制下,角的集合与实数集R之间建立起一一对应的关系:每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应
3、例题讲解
3、例题讲解
解:∵1=(180/π)0
∴3.14=3.14× (180/π)0
≈179.9090
3、例题讲解
3、例题讲解
P10 练习 1~4
判断正误:
(1)小于900的角为锐角
(2)第二象限角必大于第一象限角
1、角的度量
角度制
角可以用度为单位进行度量,1度的角等于周角的1/360。这种用度作为单位来度量角的单位制叫做角度制。
在角度制下,当把两个带着度、分、秒
单位的角相加、相减时,运算进率是什么进
制的?那么我们能否重新选择角单位?
思考:
弧度制
我们把长度等于半径长的弧所对的圆心角叫做1弧度的角,用符号rad表示,读作弧度。这种用弧度作为单位度量角的单位制叫做弧度制。
若弧是一个半圆,则其圆心角的弧度数是多少?若弧是一个整圆呢?
r
r
弧度制
注:
“弧度”不是弧长,它是一个比值。值有正负。
一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0,如果半径为r的圆的圆心角a所对弧的长为l,那么,角a的弧度数的绝对值是 | a | = l / r
a的正负由角a的终边的旋转方向决定。
r
l
a
完成课本P7 探究
弧AB的长 OB旋转的方向 ∠AOB的弧度数 ∠AOB的度数
∏r 逆时针方向 ∏ 1800
2∏r 逆时针 2∏ 3600
r 逆时针 1 57.30
2r 顺时针 -2 -114.60
∏r 顺时针 - ∏ -1800
0 未作旋转 0 00
∏r 逆时针 ∏ 1800
2∏r 逆时针 2∏ 3600
2、角度与弧度之间的换算
把角度换算成弧度
把弧度换算成角度
角度与弧度之间的换算
填写下列特殊角的度数和弧度数的对应表。
角度
弧度
2、角度与弧度之间的换算
正角
零角
负角
正实数
0
负实数
任意角的集合
实数集R
角的概念推广后,在弧度制下,角的集合与实数集R之间建立起一一对应的关系:每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应
3、例题讲解
3、例题讲解
解:∵1=(180/π)0
∴3.14=3.14× (180/π)0
≈179.9090
3、例题讲解
3、例题讲解
P10 练习 1~4
判断正误:
(1)小于900的角为锐角
(2)第二象限角必大于第一象限角
