2.2.3向量的数乘运算及其几何意义
文档属性
| 名称 | 2.2.3向量的数乘运算及其几何意义 |  | |
| 格式 | zip | ||
| 文件大小 | 177.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-05 18:05:22 | ||
图片预览






文档简介
(共16张PPT)
2.2.3 向量的数乘运算及其几何意义
实际背景
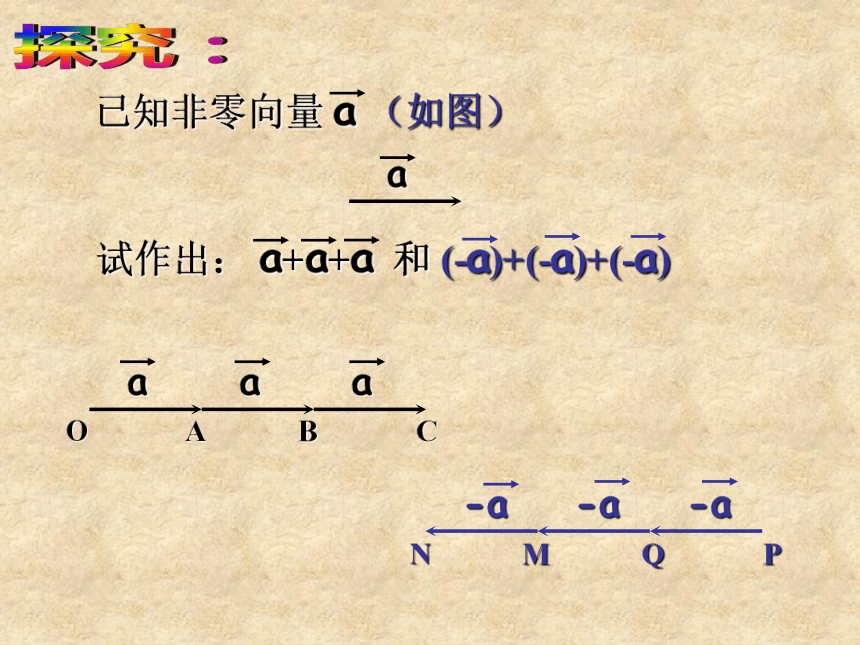
试作出: a+a+a 和 (-a)+(-a)+(-a)
已知非零向量 a (如图)
a
a
a
a
O
A
B
C
-a
-a
-a
P
Q
M
N
一、向量的数乘运算的定义:
=
(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。
(2) 已知向量 a,b,求作向量2(a+b)和2a+2b,并进行比较。
向量的数乘运算满足如下运算律:
对于向量 a (a≠0), b ,以及实数λ。
问题1:如果 b=λa
那么,向量a与b是否共线?
问题2:如果 向量a与b共线
那么,b=λa ?
向量 b 与非零向量 a 共线的充要条件是
有且只有一个实数λ,使得 b=λa
O
A
B
C
如图,在平行四边形ABCD中,点M是AB中点,点
N在线段BD上,且有BN= BD,求证:M、N、C
三点共线。
提示:设AB = a BC = b
则MN= … = a + b
MC= … = a+ b
小结回顾
二、定理的应用:
1. 证明 向量共线
2. 证明 三点共线: AB=λBC A,B,C三点共线
3. 证明 两直线平行:
AB=λCD AB∥CD
AB与CD不在同一直线上
直线AB∥直线CD
一、①λa 的定义及运算律
②向量共线定理 (a≠0)
b=λa 向量a与b共线
例4 如图,已知AD=3AB,DE=3BC,
试判断AC与AE是否共线。
∴ 与 共线.
解:
解:(1)
(2)
2.2.3 向量的数乘运算及其几何意义
实际背景
试作出: a+a+a 和 (-a)+(-a)+(-a)
已知非零向量 a (如图)
a
a
a
a
O
A
B
C
-a
-a
-a
P
Q
M
N
一、向量的数乘运算的定义:
=
(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。
(2) 已知向量 a,b,求作向量2(a+b)和2a+2b,并进行比较。
向量的数乘运算满足如下运算律:
对于向量 a (a≠0), b ,以及实数λ。
问题1:如果 b=λa
那么,向量a与b是否共线?
问题2:如果 向量a与b共线
那么,b=λa ?
向量 b 与非零向量 a 共线的充要条件是
有且只有一个实数λ,使得 b=λa
O
A
B
C
如图,在平行四边形ABCD中,点M是AB中点,点
N在线段BD上,且有BN= BD,求证:M、N、C
三点共线。
提示:设AB = a BC = b
则MN= … = a + b
MC= … = a+ b
小结回顾
二、定理的应用:
1. 证明 向量共线
2. 证明 三点共线: AB=λBC A,B,C三点共线
3. 证明 两直线平行:
AB=λCD AB∥CD
AB与CD不在同一直线上
直线AB∥直线CD
一、①λa 的定义及运算律
②向量共线定理 (a≠0)
b=λa 向量a与b共线
例4 如图,已知AD=3AB,DE=3BC,
试判断AC与AE是否共线。
∴ 与 共线.
解:
解:(1)
(2)
