2.3.1平面向量的基本定理
图片预览




文档简介
(共22张PPT)
2.3.1平面向量的基本定理
温故知新
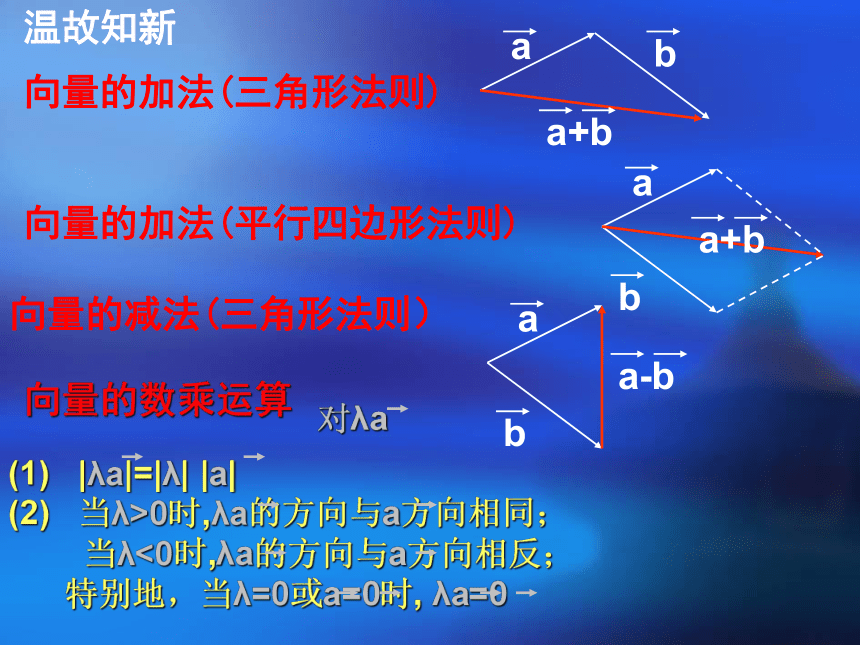
向量的加法(三角形法则)
a
b
a+b
a
b
a+b
向量的加法(平行四边形法则)
向量的减法(三角形法则)
a
b
a-b
向量的数乘运算
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0或a=0时, λa=0
对λa
设a,b为任意向量,λ,μ为任意实数,则有:
①λ(μa)=(λμ) a
②(λ+μ) a=λa+μa
③λ(a+b)=λa+λb
特别地:
向量 b 与非零向量 a 共线当且仅当
有且只有一个实数λ,使得 b=λa
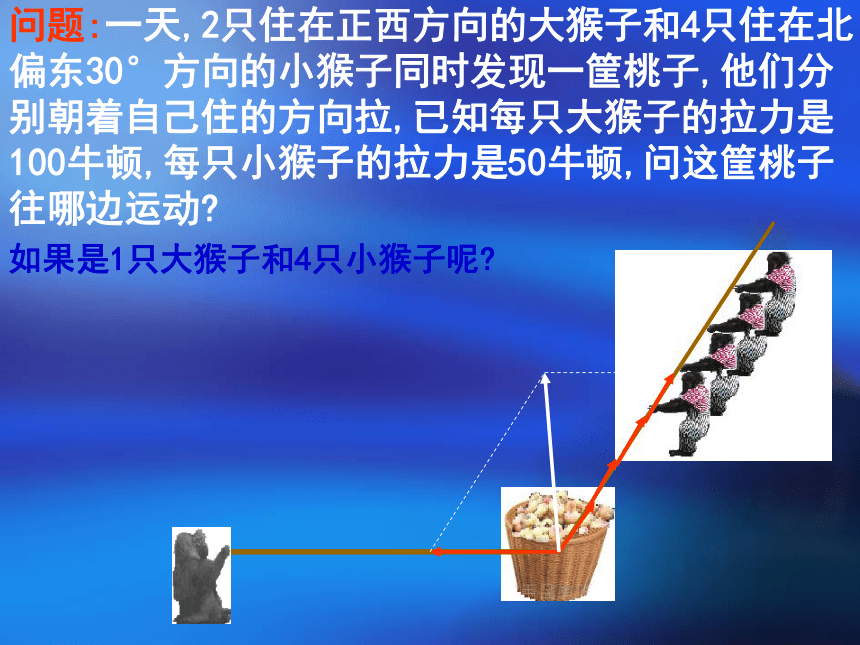
问题:一天,2只住在正西方向的大猴子和4只住在北
偏东30°方向的小猴子同时发现一筐桃子,他们分
别朝着自己住的方向拉,已知每只大猴子的拉力是
100牛顿,每只小猴子的拉力是50牛顿,问这筐桃子
往哪边运动
问题:一天,2只住在正西方向的大猴子和4只住在北
偏东30°方向的小猴子同时发现一筐桃子,他们分
别朝着自己住的方向拉,已知每只大猴子的拉力是
100牛顿,每只小猴子的拉力是50牛顿,问这筐桃子
往哪边运动
如果是1只大猴子和4只小猴子呢
N
M
e1
e2
a
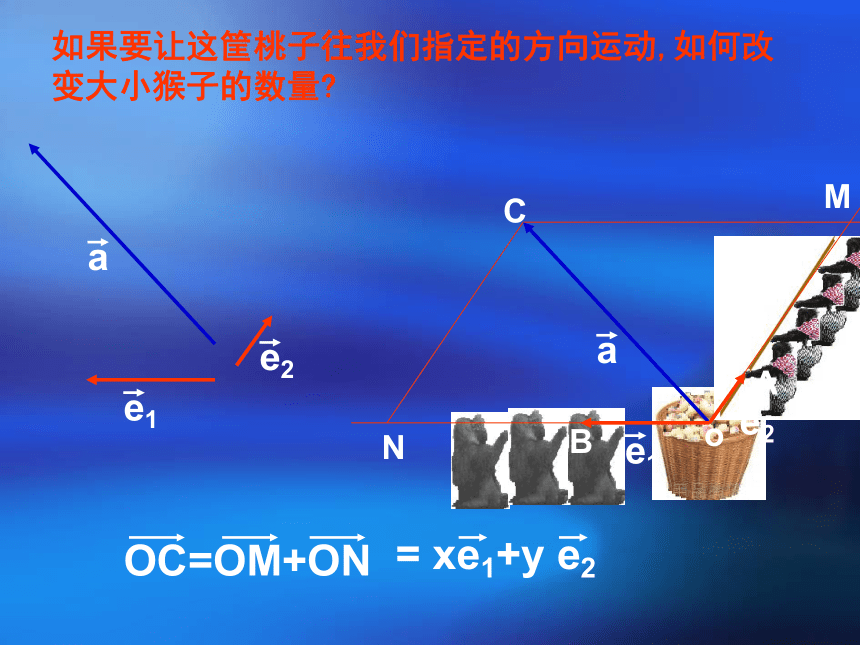
如果要让这筐桃子往我们指定的方向运动,如何改变大小猴子的数量
a
C
e1
e2
o
B
A
OC=OM+ON
= xe1+y e2
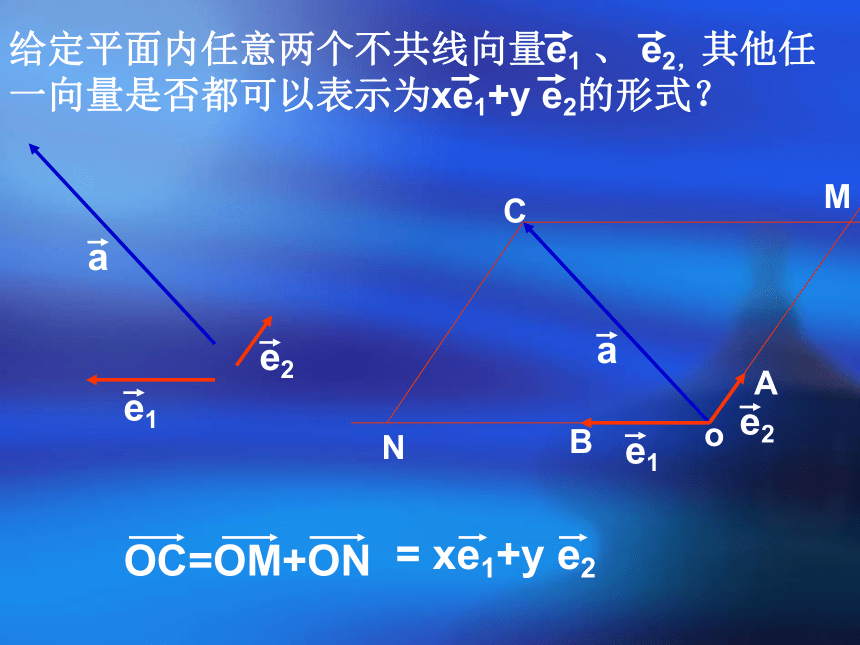
给定平面内任意两个不共线向量e1 、 e2,其他任
一向量是否都可以表示为xe1+y e2的形式?
N
M
a
C
e1
e2
o
B
A
OC=OM+ON
= xe1+y e2
e1
e2
a
如果 , 是同一平面内的两个不共线的
向量,那么对于这一平面内的任一向量 ,
有且只有一对实数 1、 2使
= 1 + 2
其中不共线的向量 , 叫做表示这一平面内的所有向量的一组基底。
平面向量的基本定理
o
C
a
N
M
F
E
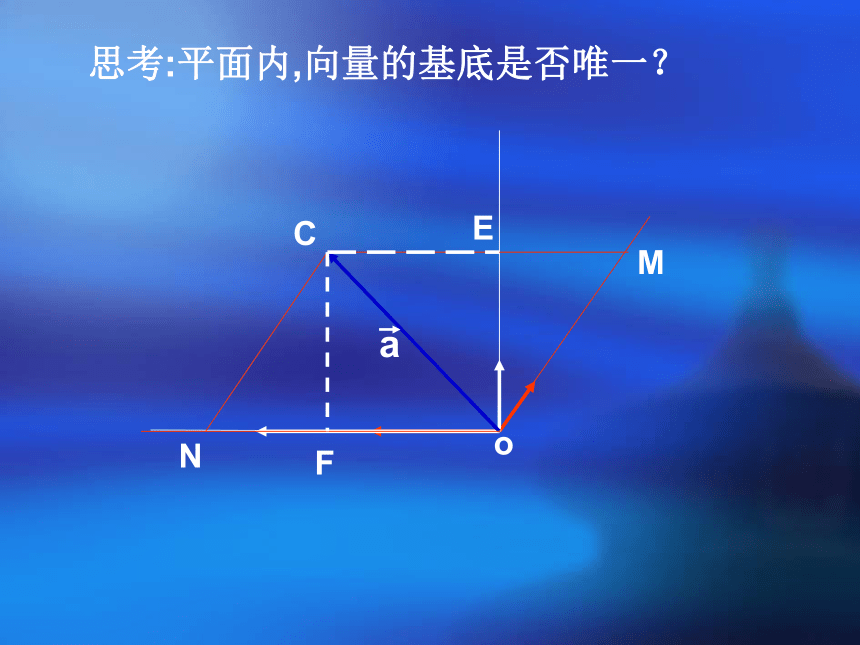
思考:平面内,向量的基底是否唯一?
例1已知向量e1,e2,求作向量-2.5e1+3e2 .
于是OC就是所求作的向量.
(2)作 OACB.
e1
e2
O
C
作法:(1)任取一点o,
作OA=-2.5e1,OB=3e2
-2.5e1
A
B
3e2
e1
e2
a
N
M
e1
e2
o
a
C
OC=OM+ON
= xe1+y e2
平行四边形做法唯一,所以实数对x,y存在唯一
对定理的理解:
1)基底: 不共线的向量e1 e2。
同一平面可以有不同基底
2)平面内的任一向量都可以沿两个不共线的
方向分解成两个向量的和的形式;
3)分解是唯一的
思考:一天,1只住在正西方向的大猴子和住在北
偏东30°方向的小猴子同时发现一筐桃子,他们分
别朝着自己住的方向拉,已知每只大猴子的拉力是
100牛顿,每只小猴子的拉力是50牛顿,问这筐桃子
往正北运动,要几只小猴子
30°
?
30°
向量的夹角
已知两个非零向量a和b如图,
则∠AOB=θ (0 ° ≤θ≤180°)
叫做向量的夹角
当θ =0° 时,a与b同向
当θ =180°时, a与b反向
a与b的夹角是90 °,则a与b垂直,记作a ⊥ b
o
B
A
a
b
共起点
A
B
C
思考:正△ABC中,向量
AB与BC的夹角为几度
D
应用:
平面内的所有向量都可以用一组基底来表示,这为
我们用向量解决问题提供了一种基本思想方法:
将其他向量化到基底上进行运算,证明.
例2.如图,在平行四边形ABCD中,点M在AB延长
线上,AB=BM,点N是BC中点,用向量方法证明:
M、N、D三点共线
A
B
M
C
N
D
例3. 设 a、b是两个不共线的向量,
已知AB = 2a + kb, CB = a + 3b,
CD = 2a – b,若A、B、D三点共线,求k的值。
把一个向量分解为两个垂直的向量,叫做把向量正交分解。
a =xi + yj.
有且只有一对实
数x、y,使得
分别与x 轴、y 轴方向相同的两单位向量i 、j 能否作
为基底?
O
x
y
i
j
任一向量a ,用这组基底可表示为
a
(x,y)叫做向量a的坐标,记作
a=( x , y )
那么i =( , )
j =( , )
0 =( , )
1 0
0 1
0 0
例4.如图,用基底i ,j 分别表示向量a、b 、
c 、d ,并求它们的坐标.
A
A2
A1
课堂小结:
1.平面向量的基本定理 (书本94页)
如果e1,e2是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量a ,有且只有一对实数 1、 2使
a = 1 e1+ 2e2
2.向量的夹角:共起点的两个向量形成的角
4.向量的坐标表示
3.基本定理的应用
e1+ μe2= xe1+ ye2
把一个向量分解为两个垂直的向量,叫做把向量正交分解。
分别与x 轴、y 轴方向相同的两单位向量i 、j 作为基底,任一向
量a ,用这组基底可表示为a =xi + yj, (x,y)叫做向量a的坐标
作业布置
P102 B组 3 4
P101 A组 1
e1
e2
a
e1
e2
a
e1
e2
a
e1
e2
a
2.3.1平面向量的基本定理
温故知新
向量的加法(三角形法则)
a
b
a+b
a
b
a+b
向量的加法(平行四边形法则)
向量的减法(三角形法则)
a
b
a-b
向量的数乘运算
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0或a=0时, λa=0
对λa
设a,b为任意向量,λ,μ为任意实数,则有:
①λ(μa)=(λμ) a
②(λ+μ) a=λa+μa
③λ(a+b)=λa+λb
特别地:
向量 b 与非零向量 a 共线当且仅当
有且只有一个实数λ,使得 b=λa
问题:一天,2只住在正西方向的大猴子和4只住在北
偏东30°方向的小猴子同时发现一筐桃子,他们分
别朝着自己住的方向拉,已知每只大猴子的拉力是
100牛顿,每只小猴子的拉力是50牛顿,问这筐桃子
往哪边运动
问题:一天,2只住在正西方向的大猴子和4只住在北
偏东30°方向的小猴子同时发现一筐桃子,他们分
别朝着自己住的方向拉,已知每只大猴子的拉力是
100牛顿,每只小猴子的拉力是50牛顿,问这筐桃子
往哪边运动
如果是1只大猴子和4只小猴子呢
N
M
e1
e2
a
如果要让这筐桃子往我们指定的方向运动,如何改变大小猴子的数量
a
C
e1
e2
o
B
A
OC=OM+ON
= xe1+y e2
给定平面内任意两个不共线向量e1 、 e2,其他任
一向量是否都可以表示为xe1+y e2的形式?
N
M
a
C
e1
e2
o
B
A
OC=OM+ON
= xe1+y e2
e1
e2
a
如果 , 是同一平面内的两个不共线的
向量,那么对于这一平面内的任一向量 ,
有且只有一对实数 1、 2使
= 1 + 2
其中不共线的向量 , 叫做表示这一平面内的所有向量的一组基底。
平面向量的基本定理
o
C
a
N
M
F
E
思考:平面内,向量的基底是否唯一?
例1已知向量e1,e2,求作向量-2.5e1+3e2 .
于是OC就是所求作的向量.
(2)作 OACB.
e1
e2
O
C
作法:(1)任取一点o,
作OA=-2.5e1,OB=3e2
-2.5e1
A
B
3e2
e1
e2
a
N
M
e1
e2
o
a
C
OC=OM+ON
= xe1+y e2
平行四边形做法唯一,所以实数对x,y存在唯一
对定理的理解:
1)基底: 不共线的向量e1 e2。
同一平面可以有不同基底
2)平面内的任一向量都可以沿两个不共线的
方向分解成两个向量的和的形式;
3)分解是唯一的
思考:一天,1只住在正西方向的大猴子和住在北
偏东30°方向的小猴子同时发现一筐桃子,他们分
别朝着自己住的方向拉,已知每只大猴子的拉力是
100牛顿,每只小猴子的拉力是50牛顿,问这筐桃子
往正北运动,要几只小猴子
30°
?
30°
向量的夹角
已知两个非零向量a和b如图,
则∠AOB=θ (0 ° ≤θ≤180°)
叫做向量的夹角
当θ =0° 时,a与b同向
当θ =180°时, a与b反向
a与b的夹角是90 °,则a与b垂直,记作a ⊥ b
o
B
A
a
b
共起点
A
B
C
思考:正△ABC中,向量
AB与BC的夹角为几度
D
应用:
平面内的所有向量都可以用一组基底来表示,这为
我们用向量解决问题提供了一种基本思想方法:
将其他向量化到基底上进行运算,证明.
例2.如图,在平行四边形ABCD中,点M在AB延长
线上,AB=BM,点N是BC中点,用向量方法证明:
M、N、D三点共线
A
B
M
C
N
D
例3. 设 a、b是两个不共线的向量,
已知AB = 2a + kb, CB = a + 3b,
CD = 2a – b,若A、B、D三点共线,求k的值。
把一个向量分解为两个垂直的向量,叫做把向量正交分解。
a =xi + yj.
有且只有一对实
数x、y,使得
分别与x 轴、y 轴方向相同的两单位向量i 、j 能否作
为基底?
O
x
y
i
j
任一向量a ,用这组基底可表示为
a
(x,y)叫做向量a的坐标,记作
a=( x , y )
那么i =( , )
j =( , )
0 =( , )
1 0
0 1
0 0
例4.如图,用基底i ,j 分别表示向量a、b 、
c 、d ,并求它们的坐标.
A
A2
A1
课堂小结:
1.平面向量的基本定理 (书本94页)
如果e1,e2是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量a ,有且只有一对实数 1、 2使
a = 1 e1+ 2e2
2.向量的夹角:共起点的两个向量形成的角
4.向量的坐标表示
3.基本定理的应用
e1+ μe2= xe1+ ye2
把一个向量分解为两个垂直的向量,叫做把向量正交分解。
分别与x 轴、y 轴方向相同的两单位向量i 、j 作为基底,任一向
量a ,用这组基底可表示为a =xi + yj, (x,y)叫做向量a的坐标
作业布置
P102 B组 3 4
P101 A组 1
e1
e2
a
e1
e2
a
e1
e2
a
e1
e2
a
