2.3.2 平面向量的正交分解及坐标表示
文档属性
| 名称 | 2.3.2 平面向量的正交分解及坐标表示 |  | |
| 格式 | zip | ||
| 文件大小 | 67.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-05 18:05:22 | ||
图片预览


文档简介
(共23张PPT)
2.3.2 平面向量的正交分解及坐标表示
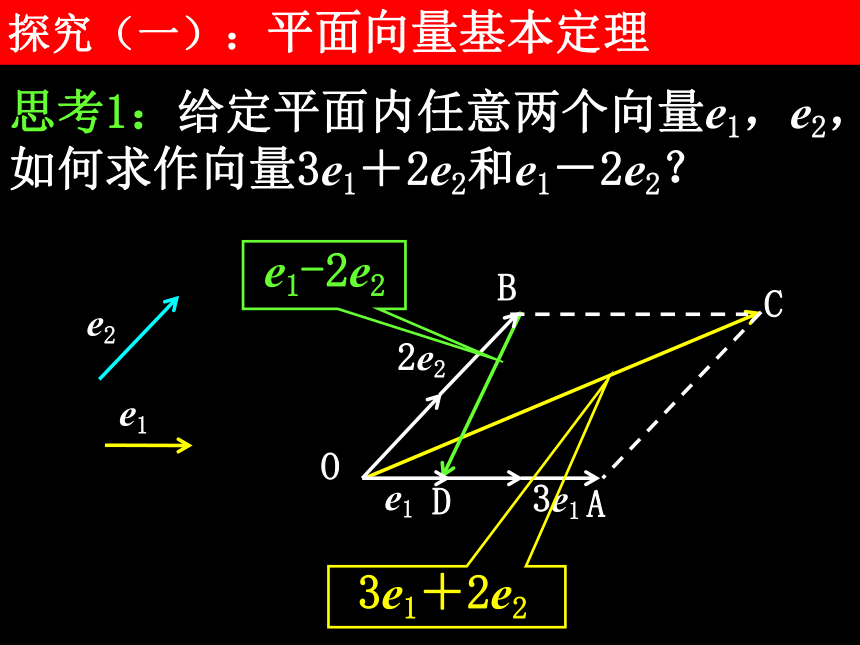
探究(一):平面向量基本定理
思考1:给定平面内任意两个向量e1,e2,如何求作向量3e1+2e2和e1-2e2?
e1
e2
2e2
B
C
O
3e1
A
e1
D
3e1+2e2
e1-2e2
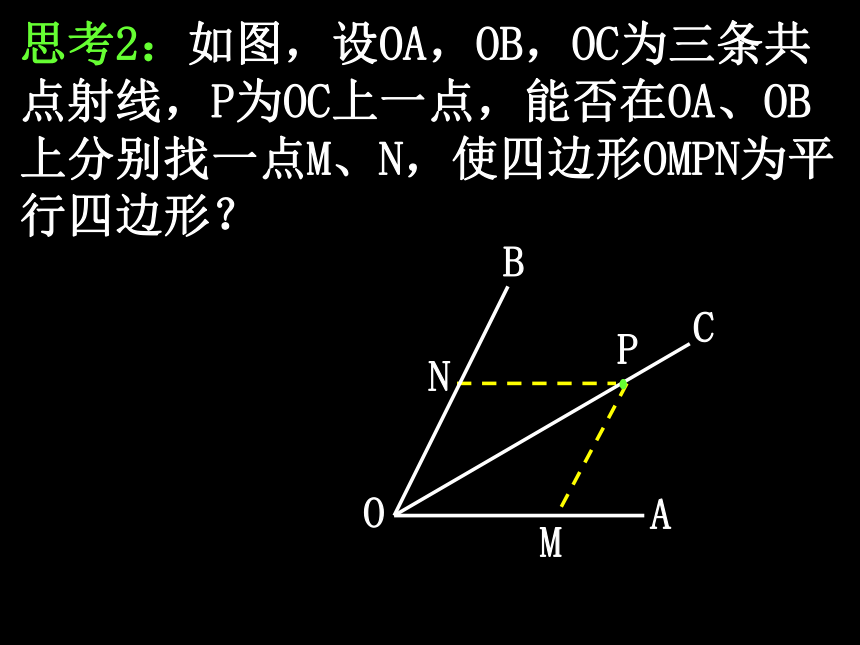
思考2:如图,设OA,OB,OC为三条共点射线,P为OC上一点,能否在OA、OB上分别找一点M、N,使四边形OMPN为平行四边形?
M
N
O
A
B
C
P
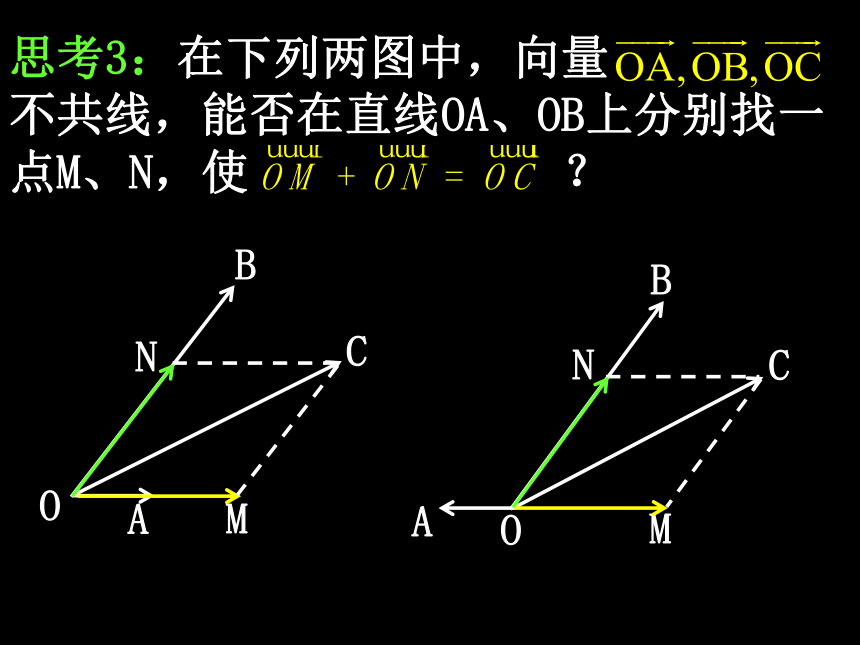
思考3:在下列两图中,向量
不共线,能否在直线OA、OB上分别找一点M、N,使 ?
O
A
B
C
M
N
O
A
B
C
M
N
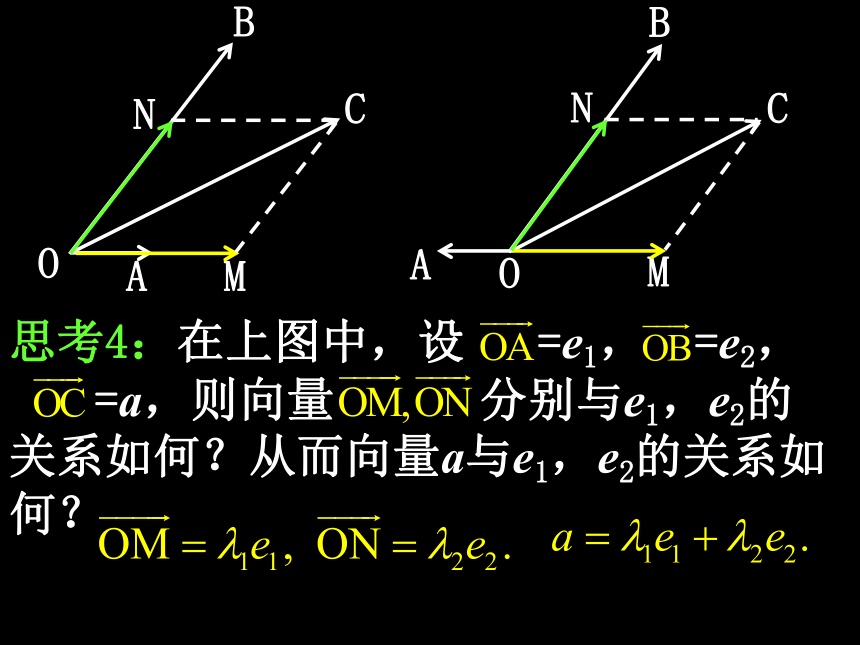
思考4:在上图中,设 =e1, =e2, =a,则向量 分别与e1,e2的关系如何?从而向量a与e1,e2的关系如何?
O
A
B
C
M
N
O
A
B
C
M
N
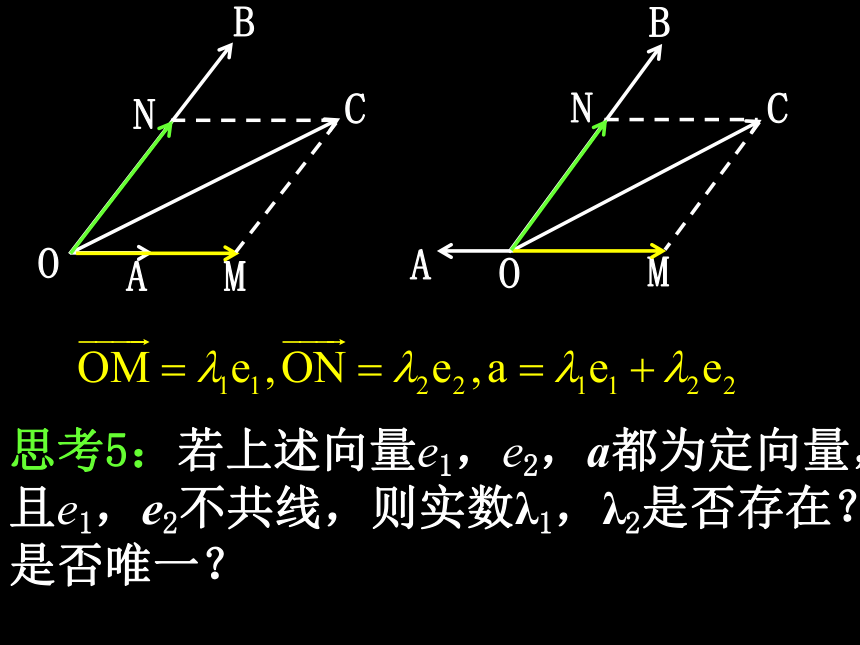
思考5:若上述向量e1,e2,a都为定向量,且e1,e2不共线,则实数λ1,λ2是否存在?是否唯一?
O
A
B
C
M
N
O
A
B
C
M
N
思考6:若向量a与e1或e2共线,a还能用λ1e1+λ2e2表示吗?
e1
a
a=λ1e1+0e2
e2
a
a=0e1+λ2e2
思考7:根据上述分析,平面内任一向量a都可以由这个平面内两个不共线的向量e1,e2表示出来,从而可形成一个定理.你能完整地描述这个定理的内容吗?
若e1、e2是同一平面内的两个不共线向量,则对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.
思考8:上述定理称为平面向量基本定理,不共线向量e1,e2叫做表示这一平面内所有向量的一组基底. 那么同一平面内可以作基底的向量有多少组?不同基底对应向量a的表示式是否相同?
若e1、e2是同一平面内的两个不共线向量,则对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.
探究(二):平面向量的正交分解及坐标表示
[0°,180°]
思考1:不共线的向量有不同的方向,对于两个非零向量a和b,作 a, b,如图.为了反映这两个向量的位置关系,称∠AOB为向量a与b的夹角.你认为向量的夹角的取值范围应如何约定为宜?
b
a
a
b
A
B
O
思考2:如果向量a与b的夹角是90°,则称向量a与b垂直,记作a⊥b. 互相垂直的两个向量能否作为平面内所有向量的一组基底?
b
a
思考3:把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.如图,向量i、j是两个互相垂直的单位向量,向量a与i的夹角是30°,且|a|=4,以向量i、j为基底,向量a如何表示?
B
a
i
O
j
A
P
思考4:在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i、j作为基底,对于平面内的一个向量a,由平面向量基本定理知,有且只有一对实数x、y,使得 a=xi+yj.我们把有序数对(x,y)叫做向量a的坐标,记作a=(x,y).其中x叫做a在x轴上的坐标,y叫做a在y轴
上的坐标,上式叫做向量
的坐标表示.那么x、y的
几何意义如何?
a
i
x
y
O
j
x
y
思考5:相等向量的坐标必然相等,作向量 a,则 (x,y),此时点A是坐标是什么?
A
a
i
x
y
O
j
A(x,y)
理论迁移
例1 如图,已知向量e1、e2,求作向量-2.5e1+3e2.
e1
e2
C
O
A
-2.5e1
B
3e2
例2 如图,写出向量a,b,c,d的坐标.
2
4
5
2
a
b
c
d
-4
-2
-5
-2
x
y
O
a=(2,3)
b=(-2,3)
c=(-2,-3)
d=(2,-3)
例3 如图,在平行四边形ABCD中,
=a, =b,E、M分别是AD、DC的中点,点F在BC上,且BC=3BF,以a,b为基底分别表示向量 和 .
A
B
E
D
C
F
M
小结作业
1.平面向量基本定理是建立在向量加法和数乘运算基础上的向量分解原理,同时又是向量坐标表示的理论依据,是一个承前起后的重要知识点.
2.向量的夹角是反映两个向量相对位置关系的一个几何量,平行向量的夹角是0°或180°,垂直向量的夹角是90°.
3.向量的坐标表示是一种向量与坐标的对应关系,它使得向量具有代数意义.将向量的起点平移到坐标原点,则平移后向量的终点坐标就是向量的坐标.
作业:
P102习题2.3B组:3,4.
2.3.2 平面向量的正交分解及坐标表示
探究(一):平面向量基本定理
思考1:给定平面内任意两个向量e1,e2,如何求作向量3e1+2e2和e1-2e2?
e1
e2
2e2
B
C
O
3e1
A
e1
D
3e1+2e2
e1-2e2
思考2:如图,设OA,OB,OC为三条共点射线,P为OC上一点,能否在OA、OB上分别找一点M、N,使四边形OMPN为平行四边形?
M
N
O
A
B
C
P
思考3:在下列两图中,向量
不共线,能否在直线OA、OB上分别找一点M、N,使 ?
O
A
B
C
M
N
O
A
B
C
M
N
思考4:在上图中,设 =e1, =e2, =a,则向量 分别与e1,e2的关系如何?从而向量a与e1,e2的关系如何?
O
A
B
C
M
N
O
A
B
C
M
N
思考5:若上述向量e1,e2,a都为定向量,且e1,e2不共线,则实数λ1,λ2是否存在?是否唯一?
O
A
B
C
M
N
O
A
B
C
M
N
思考6:若向量a与e1或e2共线,a还能用λ1e1+λ2e2表示吗?
e1
a
a=λ1e1+0e2
e2
a
a=0e1+λ2e2
思考7:根据上述分析,平面内任一向量a都可以由这个平面内两个不共线的向量e1,e2表示出来,从而可形成一个定理.你能完整地描述这个定理的内容吗?
若e1、e2是同一平面内的两个不共线向量,则对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.
思考8:上述定理称为平面向量基本定理,不共线向量e1,e2叫做表示这一平面内所有向量的一组基底. 那么同一平面内可以作基底的向量有多少组?不同基底对应向量a的表示式是否相同?
若e1、e2是同一平面内的两个不共线向量,则对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.
探究(二):平面向量的正交分解及坐标表示
[0°,180°]
思考1:不共线的向量有不同的方向,对于两个非零向量a和b,作 a, b,如图.为了反映这两个向量的位置关系,称∠AOB为向量a与b的夹角.你认为向量的夹角的取值范围应如何约定为宜?
b
a
a
b
A
B
O
思考2:如果向量a与b的夹角是90°,则称向量a与b垂直,记作a⊥b. 互相垂直的两个向量能否作为平面内所有向量的一组基底?
b
a
思考3:把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.如图,向量i、j是两个互相垂直的单位向量,向量a与i的夹角是30°,且|a|=4,以向量i、j为基底,向量a如何表示?
B
a
i
O
j
A
P
思考4:在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i、j作为基底,对于平面内的一个向量a,由平面向量基本定理知,有且只有一对实数x、y,使得 a=xi+yj.我们把有序数对(x,y)叫做向量a的坐标,记作a=(x,y).其中x叫做a在x轴上的坐标,y叫做a在y轴
上的坐标,上式叫做向量
的坐标表示.那么x、y的
几何意义如何?
a
i
x
y
O
j
x
y
思考5:相等向量的坐标必然相等,作向量 a,则 (x,y),此时点A是坐标是什么?
A
a
i
x
y
O
j
A(x,y)
理论迁移
例1 如图,已知向量e1、e2,求作向量-2.5e1+3e2.
e1
e2
C
O
A
-2.5e1
B
3e2
例2 如图,写出向量a,b,c,d的坐标.
2
4
5
2
a
b
c
d
-4
-2
-5
-2
x
y
O
a=(2,3)
b=(-2,3)
c=(-2,-3)
d=(2,-3)
例3 如图,在平行四边形ABCD中,
=a, =b,E、M分别是AD、DC的中点,点F在BC上,且BC=3BF,以a,b为基底分别表示向量 和 .
A
B
E
D
C
F
M
小结作业
1.平面向量基本定理是建立在向量加法和数乘运算基础上的向量分解原理,同时又是向量坐标表示的理论依据,是一个承前起后的重要知识点.
2.向量的夹角是反映两个向量相对位置关系的一个几何量,平行向量的夹角是0°或180°,垂直向量的夹角是90°.
3.向量的坐标表示是一种向量与坐标的对应关系,它使得向量具有代数意义.将向量的起点平移到坐标原点,则平移后向量的终点坐标就是向量的坐标.
作业:
P102习题2.3B组:3,4.
