2.3.3平面向量的坐标运算
图片预览






文档简介
(共19张PPT)
平面向量的坐标运算
平面向量的坐标运算
1
2
3
4
-1
-5
-2
-3
-4
x
y
5
0
1
2
3
4
-1
-2
-3
-4
o
问题:
若已知 =(1 ,3) , =(5 ,1),
a
b
如何求 + , - 的坐标呢?
a
b
a
b
a
b
C
(6,4)
结论、平面向量的坐标运算法则
- =(x1-x2 ,y1-y2)
b
a
(x1,y1)
(x2,y2)
+
b
a
=(x1 +y1 )
+(x2 +y2 )
=(x1 + x2 ) + ( y1+ y2 )
平面向量的坐标运算
猜想:
+ =(x1+x2 ,y1+y2)
b
a
证明:
=(x1 , ) + ( , y2 )
=(x1 +y1 )
+(x2 +y2 )
重点
平面向量的坐标运算
向量 的 数
乘运算
?
平面向量的坐标运算
平面向量的坐标运算法则
重点
平面向量的坐标运算
例
(-1,5)
平面向量坐标运算法则应用
(5,-3)
(-6,19)
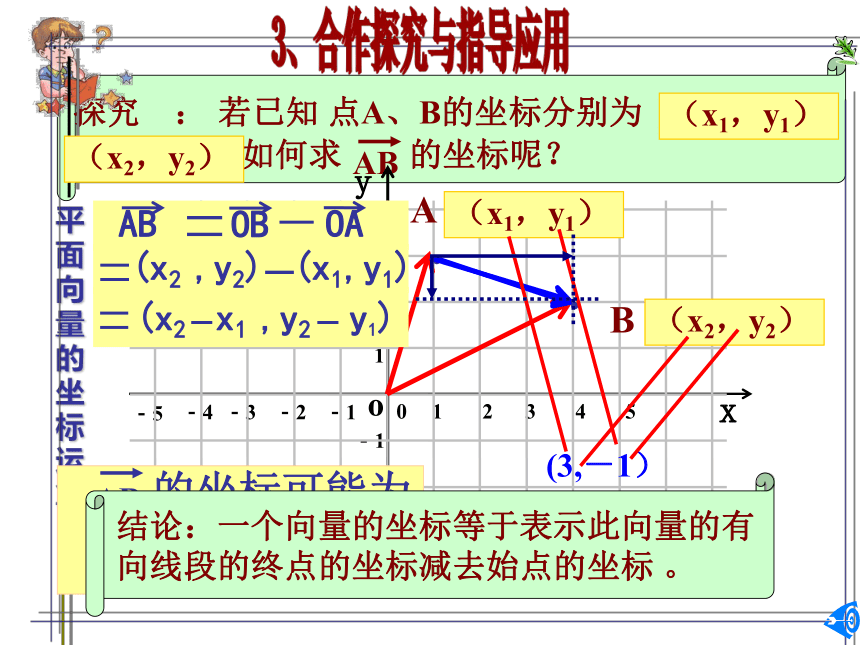
探究 : 若已知 点A、B的坐标分别为 (1,3), (4,2),如何求 的坐标呢?
AB
1
2
3
4
-1
返回
-5
-2
-3
-4
x
y
5
0
1
2
3
4
-1
-2
-3
-4
o
平面向量的坐标运算
(3,-1)
的坐标可能为
(x2-x1 , y2-y1)
AB
B(4,2)
A(1,3)
·
·
(x1,y1)
(x2,y2)
(x1,y1)
(x2,y2)
AB
OA
OB
(x2 x1 ,y2 y1)
(x2 ,y2)
(x1,y1)
结论:一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标 。
平面向量的坐标运算
例2
已知A、B两点的坐标,求 ,
的坐标。
⑴ A (3,5) , B (6,9) ; ⑵ A(-3,4) , B(6,3)
⑶ A (0,3) , B (0,5) ; ⑷ A (3,0), B(8,0)
AB
BA
平面向量的坐标运算
AB
终点B
始点A
终点坐标减去始点坐标
( -2 , 7 )
终点坐标减去向量坐标
始点坐标加上向量坐标
( 3 , -4 )
( 1,3 )
( 1,2 )
( 2,3 )
( 1,1 )
平面向量的坐标运算
例3.如图,已知 四边形 的四个顶点A、B、C,D的坐标分别是(-2,1)、(-1,3)、(3,4),(2,2)求证四边形 ABCD是平行四边形
平面向量的坐标运算
1
2
3
4
5
x
y
5
0
1
2
3
4
-1
-1
-2
-2
-3
-4
-5
C
A
B
D
-6
6
例3.如图,已知 四边形 的四个顶点A、B、C,D的坐标分别是(-2,1)、(-1,3)、(3,4),(2,2)求证四边形 ABCD是平行四边形
平面向量的坐标运算
思考1已知 ABCD的三个顶点A、B、C的坐
标分别为(-2,1)、(-1,3)、(3,4),
求顶点D的坐标。
平面向量的坐标运算
1
2
3
4
5
x
y
5
0
1
2
3
4
-1
-1
-2
-2
-3
-4
-5
C
A
B
D
-6
6
思考1已知 ABCD的三个顶点A、B、C的坐
标分别为(-2,1)、(-1,3)、(3,4),
求顶点D的坐标。
平面向量的坐标运算
A
B
C
D
x
y
O
解:设点D的坐标为(x,y)
解得 x=2,y=2
所以顶点D的坐标为(2,2)
思考1已知 ABCD的三个顶点A、B、C的坐
标分别为(-2,1)、(-1,3)、(3,4),
求顶点D的坐标。
平面向量的坐标运算
思考1已知 ABCD的三个顶点A、B、C的坐
标分别为(-2,1)、(-1,3)、(3,4),
求顶点D的坐标。
A
B
C
D
x
y
O
另解:由平行四边形法则可得
而
所以顶点D的坐标为(2,2)
平面向量的坐标运算
思考1已知 ABCD的三个顶点A、B、C的坐
标分别为(-2,1)、(-1,3)、(3,4),
求顶点D的坐标。
思考2:若已知平面上三个点A、B、C 的坐标分别为(-2,1),(-1,3),(3,4),求第四个点的坐标,使这四个点构成一个平行四边形的四个顶点.
ABCD
平面向量的坐标运算
1
2
3
4
5
x
y
5
0
1
2
3
4
-1
-1
-2
-2
-3
-4
-5
C
A
B
D
-6
6
D1
D2
D
平面向量的坐标运算
小结回顾
请回顾本堂课的教学过程,你能说说你学了哪些知识吗?
1.平面向量坐标的加.减运算法则
=( x1 , y1) + (x2 , y2)= (x1+x2 , y1+y2)
=( x1 , y1) - (x2 , y2)= (x1- x2 , y1-y2)
2.平面向量坐标实数与向量相乘的运算法则
3.平面向量坐标
若A(x1 , y1) , B(x2 , y2)
则 =(x2 - x1 , y2 – y1 )
=( x1 , y1) + (x2 , y2)= (x1+x2 , y1+y2)
平面向量的坐标运算
课 后 作 业
平面向量的坐标运算
平面向量的坐标运算
1
2
3
4
-1
-5
-2
-3
-4
x
y
5
0
1
2
3
4
-1
-2
-3
-4
o
问题:
若已知 =(1 ,3) , =(5 ,1),
a
b
如何求 + , - 的坐标呢?
a
b
a
b
a
b
C
(6,4)
结论、平面向量的坐标运算法则
- =(x1-x2 ,y1-y2)
b
a
(x1,y1)
(x2,y2)
+
b
a
=(x1 +y1 )
+(x2 +y2 )
=(x1 + x2 ) + ( y1+ y2 )
平面向量的坐标运算
猜想:
+ =(x1+x2 ,y1+y2)
b
a
证明:
=(x1 , ) + ( , y2 )
=(x1 +y1 )
+(x2 +y2 )
重点
平面向量的坐标运算
向量 的 数
乘运算
?
平面向量的坐标运算
平面向量的坐标运算法则
重点
平面向量的坐标运算
例
(-1,5)
平面向量坐标运算法则应用
(5,-3)
(-6,19)
探究 : 若已知 点A、B的坐标分别为 (1,3), (4,2),如何求 的坐标呢?
AB
1
2
3
4
-1
返回
-5
-2
-3
-4
x
y
5
0
1
2
3
4
-1
-2
-3
-4
o
平面向量的坐标运算
(3,-1)
的坐标可能为
(x2-x1 , y2-y1)
AB
B(4,2)
A(1,3)
·
·
(x1,y1)
(x2,y2)
(x1,y1)
(x2,y2)
AB
OA
OB
(x2 x1 ,y2 y1)
(x2 ,y2)
(x1,y1)
结论:一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标 。
平面向量的坐标运算
例2
已知A、B两点的坐标,求 ,
的坐标。
⑴ A (3,5) , B (6,9) ; ⑵ A(-3,4) , B(6,3)
⑶ A (0,3) , B (0,5) ; ⑷ A (3,0), B(8,0)
AB
BA
平面向量的坐标运算
AB
终点B
始点A
终点坐标减去始点坐标
( -2 , 7 )
终点坐标减去向量坐标
始点坐标加上向量坐标
( 3 , -4 )
( 1,3 )
( 1,2 )
( 2,3 )
( 1,1 )
平面向量的坐标运算
例3.如图,已知 四边形 的四个顶点A、B、C,D的坐标分别是(-2,1)、(-1,3)、(3,4),(2,2)求证四边形 ABCD是平行四边形
平面向量的坐标运算
1
2
3
4
5
x
y
5
0
1
2
3
4
-1
-1
-2
-2
-3
-4
-5
C
A
B
D
-6
6
例3.如图,已知 四边形 的四个顶点A、B、C,D的坐标分别是(-2,1)、(-1,3)、(3,4),(2,2)求证四边形 ABCD是平行四边形
平面向量的坐标运算
思考1已知 ABCD的三个顶点A、B、C的坐
标分别为(-2,1)、(-1,3)、(3,4),
求顶点D的坐标。
平面向量的坐标运算
1
2
3
4
5
x
y
5
0
1
2
3
4
-1
-1
-2
-2
-3
-4
-5
C
A
B
D
-6
6
思考1已知 ABCD的三个顶点A、B、C的坐
标分别为(-2,1)、(-1,3)、(3,4),
求顶点D的坐标。
平面向量的坐标运算
A
B
C
D
x
y
O
解:设点D的坐标为(x,y)
解得 x=2,y=2
所以顶点D的坐标为(2,2)
思考1已知 ABCD的三个顶点A、B、C的坐
标分别为(-2,1)、(-1,3)、(3,4),
求顶点D的坐标。
平面向量的坐标运算
思考1已知 ABCD的三个顶点A、B、C的坐
标分别为(-2,1)、(-1,3)、(3,4),
求顶点D的坐标。
A
B
C
D
x
y
O
另解:由平行四边形法则可得
而
所以顶点D的坐标为(2,2)
平面向量的坐标运算
思考1已知 ABCD的三个顶点A、B、C的坐
标分别为(-2,1)、(-1,3)、(3,4),
求顶点D的坐标。
思考2:若已知平面上三个点A、B、C 的坐标分别为(-2,1),(-1,3),(3,4),求第四个点的坐标,使这四个点构成一个平行四边形的四个顶点.
ABCD
平面向量的坐标运算
1
2
3
4
5
x
y
5
0
1
2
3
4
-1
-1
-2
-2
-3
-4
-5
C
A
B
D
-6
6
D1
D2
D
平面向量的坐标运算
小结回顾
请回顾本堂课的教学过程,你能说说你学了哪些知识吗?
1.平面向量坐标的加.减运算法则
=( x1 , y1) + (x2 , y2)= (x1+x2 , y1+y2)
=( x1 , y1) - (x2 , y2)= (x1- x2 , y1-y2)
2.平面向量坐标实数与向量相乘的运算法则
3.平面向量坐标
若A(x1 , y1) , B(x2 , y2)
则 =(x2 - x1 , y2 – y1 )
=( x1 , y1) + (x2 , y2)= (x1+x2 , y1+y2)
平面向量的坐标运算
课 后 作 业
