七年级数学下册第9章分式章末复习教案新版沪科版
文档属性
| 名称 | 七年级数学下册第9章分式章末复习教案新版沪科版 |
|
|
| 格式 | zip | ||
| 文件大小 | 569.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览


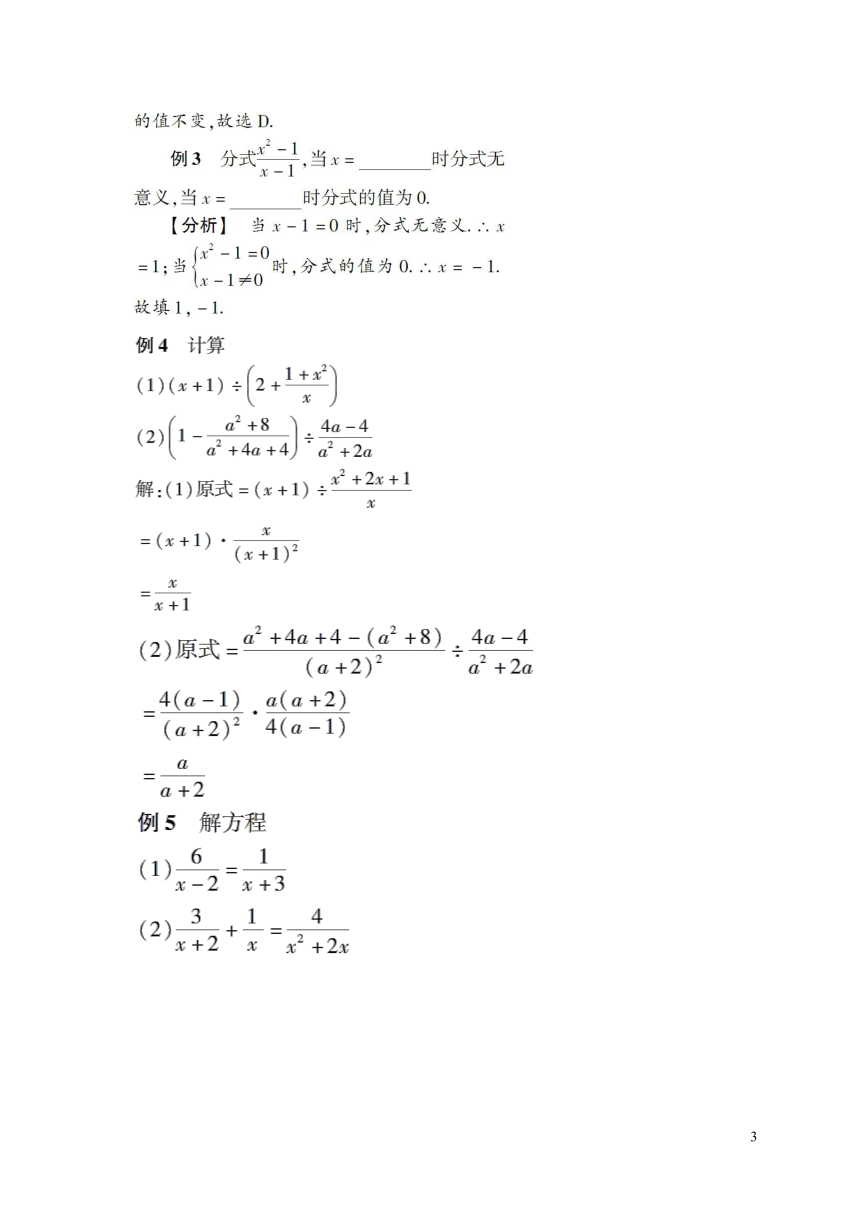
文档简介
章末复习
【知识与技能】进一步加深对分式、分式方程概念的理解,掌握分式的基本性质,会进行分式的混合运算,会解分式方程,能运用分式方程解决实际问题.
【过程与方法】
通过梳理本章知识,回顾解决问题中所涉及的类比思想,转化思想,加深学生对本章知识的理解和应用.
【情感态度】
在运用分式、分式方程的有关知识解决实际问题的过程中,进一步体会数学与生活的密切联系,增强学生的数学应用意识,激发学生学习数学的兴趣.
【教学重点】
分式的混合运算,分式方程的解法及分式方程的应用.
【教学难点】
分式方程的应用
一、情境导入,初步认识
【教学说明】引导学生回顾本章知识点,展示本章知识结构框图,使学生能系统地了解本章知识及它们之间的关系,教学时,边回顾边建立结构框图.
二、思考探究,获取新知
1.分式、分式方程有(无)意义的条件,分式值为0的条件.一般来说,a,b表示两个整式,且b中含有字母,那么式子叫做分式;b≠0,分式有意义;b=0,分式无意义;a=0且b≠0,分式的值为0.
2.分式的基本性质
分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.
3.分式的运算
两个分式相乘,用分子的积作积的分子,用分母的积作积的分母;两个分式相除,将除式的分子,分母颠倒位置后,与被除式相乘;同分母的分式相加减,分母不变,分子相加减;异分母的分式相加减,先通分,变为同分母的分式后再加减.
4.约分、通分
把一个分式的分子和分母的公因式约去叫做约分.化异分母分式为同分母分式的过程叫做通分.
5.分式方程及分式方程的解法.
分母中含有未知数的方程叫做分式方程,解分式方程的一般步骤是:(1)方程两边同乘以最简公分母,将分式方程转化为整式方程;(2)解整式方程;(3)检验.
三、典例精析,掌握新知
例8某开发公司的960件新产品需要精加工后才能投放市场,现有甲、乙两个工厂都想加工这批产品,已知甲工厂加工完这批产品比乙工厂多用20天,且甲工厂每天加工的数量是乙工厂每天加工的数量的,求甲、乙两工厂每天各能加工多少件新产品.
【解】设乙工厂每天能加工x件产品,则甲工厂每天能加工x件产品.
∴甲每天能加工16件产品,乙每天能加工24件产品.
【教学说明】教师给出例题,学生独立自主完成,数师可适当进行评讲,强调应用各知识需要注意的问题,培养学生综合运用所学知识的能力,对于例题可适当增减.
四、复习训练,巩固提高
1.下列分式是最简分式的是()
7.一项工程,乙单独完成需12天,若先由甲单独做3天,则再由甲、乙合做6天可完成任务,则甲单独做多少天可完成任务?
【教学说明】教师给出习题,学生自主完成,加深对本章知识的理解,进一步提高学生综合运用所学知识的能力.教师在巡视过程中对有困难的学生进行适当点拨.
【答案】1.C
五、师生互动,课堂小结
1.通过这节课的学习,你对本章有哪些新的认识?有何体会?请与同伴交流.
2.通过本章知识的学习,你掌握了哪些数学思想方法?说说看.
【教学说明】学生回顾本章知识,积极与同伴交流,积累解题方法和经验.
完成练习册中本课时练习.
通过知识框图的呈现,让学生更好地回顾本章的知识点,进行知识的梳理,通过例题的讲解与习题的训练,进一步提高学生分析问题,解决问题的能力,激发学生学习数学的兴趣.
1
【知识与技能】进一步加深对分式、分式方程概念的理解,掌握分式的基本性质,会进行分式的混合运算,会解分式方程,能运用分式方程解决实际问题.
【过程与方法】
通过梳理本章知识,回顾解决问题中所涉及的类比思想,转化思想,加深学生对本章知识的理解和应用.
【情感态度】
在运用分式、分式方程的有关知识解决实际问题的过程中,进一步体会数学与生活的密切联系,增强学生的数学应用意识,激发学生学习数学的兴趣.
【教学重点】
分式的混合运算,分式方程的解法及分式方程的应用.
【教学难点】
分式方程的应用
一、情境导入,初步认识
【教学说明】引导学生回顾本章知识点,展示本章知识结构框图,使学生能系统地了解本章知识及它们之间的关系,教学时,边回顾边建立结构框图.
二、思考探究,获取新知
1.分式、分式方程有(无)意义的条件,分式值为0的条件.一般来说,a,b表示两个整式,且b中含有字母,那么式子叫做分式;b≠0,分式有意义;b=0,分式无意义;a=0且b≠0,分式的值为0.
2.分式的基本性质
分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.
3.分式的运算
两个分式相乘,用分子的积作积的分子,用分母的积作积的分母;两个分式相除,将除式的分子,分母颠倒位置后,与被除式相乘;同分母的分式相加减,分母不变,分子相加减;异分母的分式相加减,先通分,变为同分母的分式后再加减.
4.约分、通分
把一个分式的分子和分母的公因式约去叫做约分.化异分母分式为同分母分式的过程叫做通分.
5.分式方程及分式方程的解法.
分母中含有未知数的方程叫做分式方程,解分式方程的一般步骤是:(1)方程两边同乘以最简公分母,将分式方程转化为整式方程;(2)解整式方程;(3)检验.
三、典例精析,掌握新知
例8某开发公司的960件新产品需要精加工后才能投放市场,现有甲、乙两个工厂都想加工这批产品,已知甲工厂加工完这批产品比乙工厂多用20天,且甲工厂每天加工的数量是乙工厂每天加工的数量的,求甲、乙两工厂每天各能加工多少件新产品.
【解】设乙工厂每天能加工x件产品,则甲工厂每天能加工x件产品.
∴甲每天能加工16件产品,乙每天能加工24件产品.
【教学说明】教师给出例题,学生独立自主完成,数师可适当进行评讲,强调应用各知识需要注意的问题,培养学生综合运用所学知识的能力,对于例题可适当增减.
四、复习训练,巩固提高
1.下列分式是最简分式的是()
7.一项工程,乙单独完成需12天,若先由甲单独做3天,则再由甲、乙合做6天可完成任务,则甲单独做多少天可完成任务?
【教学说明】教师给出习题,学生自主完成,加深对本章知识的理解,进一步提高学生综合运用所学知识的能力.教师在巡视过程中对有困难的学生进行适当点拨.
【答案】1.C
五、师生互动,课堂小结
1.通过这节课的学习,你对本章有哪些新的认识?有何体会?请与同伴交流.
2.通过本章知识的学习,你掌握了哪些数学思想方法?说说看.
【教学说明】学生回顾本章知识,积极与同伴交流,积累解题方法和经验.
完成练习册中本课时练习.
通过知识框图的呈现,让学生更好地回顾本章的知识点,进行知识的梳理,通过例题的讲解与习题的训练,进一步提高学生分析问题,解决问题的能力,激发学生学习数学的兴趣.
1
