山东省淄博市博山区万杰朝阳学校2020-2021学年下学期八年级数学期中检测卷(五四制专用)((word版无答案))
文档属性
| 名称 | 山东省淄博市博山区万杰朝阳学校2020-2021学年下学期八年级数学期中检测卷(五四制专用)((word版无答案)) |  | |
| 格式 | zip | ||
| 文件大小 | 353.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 13:07:20 | ||
图片预览


文档简介
淄博市博山区万杰朝阳学校2020-2021学年第二学期
八年级数学期中检测卷(五四制专用)
(总分:150分
时间:120分钟)
一.选择题(共48分).
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
1.下列式子中,为最简二次根式的是( )
A.
B.
C.
D.
2.用配方法解一元二次方程x24x+1=0时,下列变形正确的是( )
A.(x2)2=1
B.(x2)2=5
C.(x+2)2=3
D.(x2)2=3
3.若方程x2-2x-4=0的两个实数根为α,β,则α2+β2的值为
(
)
A.12
B.10
C.4
D.-4
4.在下列各组根式中,是同类二次根式的是(
)
A.和
B.和
C.和
D.和
5.如图,在Rt△ABC中,∠BAC=90°,AB=6,点D是斜边BC的中点,若AD=5,则AC等于
( )
第5题图
第6题图
第7题图
6.菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A的纵坐标是1,则点B的坐标是( )
A.(3,1)
B.(3,-1)
C.(1,-3)
D.(1,3)
7.
如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,若AB=6,BC=9,则BF的长为( )
A.4
B.3
C.4.5
D.5
8.
如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2
m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高约为
( )
第8题图
第11题图
第14题图
A.5.5
m
B.6.2
m
C.11
m
D.2.2
m
9.
如图,在大小为4×4的正方形网格中,是相似三角形的是(
)
10.
如图,a,b,c在数轴上的位置如图所示,化简-|a+c|+的结果为(
)
A.2c-b
B.-b
C.b
D.-2a-b
11.
如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为
( )
A.2
B.4
C.6
D.8
12.若关于x的一元二次方程(k2)x22kx+k=6有实数根,则k的取值范围为( )
A.k0
B.k0且k≠2
C.k
D.k且k≠2
二.填空题(共28分).
13.
若是二次根式,则x的值可以为
(写出一个即可).
14.
如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条平行),剩余部分栽种花草,且栽种花草的面积77m2,设道路的宽为xm,则根据题意,可列方程为_______________.
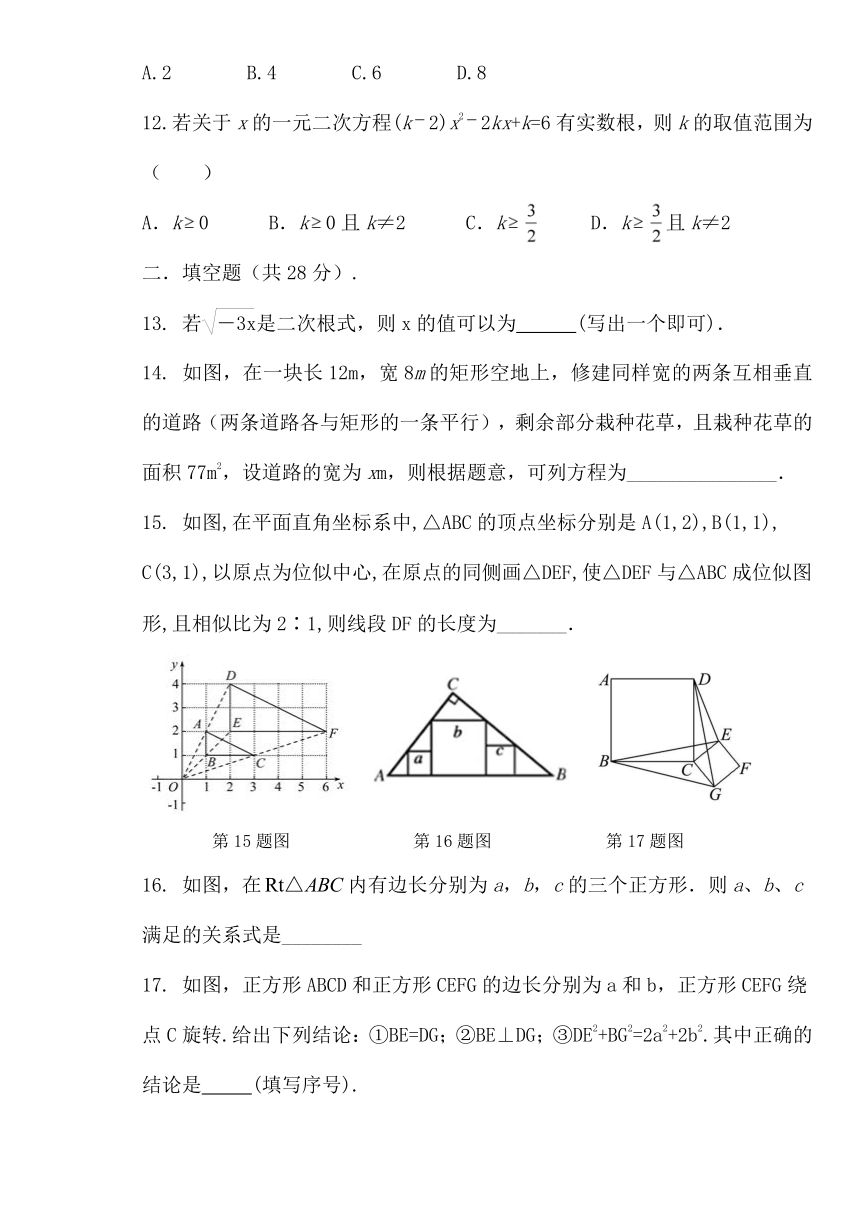
15.
如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),
C(3,1),以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2∶1,则线段DF的长度为_______.
(
第15题图
第16题图
第17题图
16.
如图,在内有边长分别为a,b,c的三个正方形.则a、b、c满足的关系式是________
17.
如图,正方形ABCD和正方形CEFG的边长分别为a和b,正方形CEFG绕点C旋转.给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2.其中正确的结论是
(填写序号).?
三.解答题(共74分).
18.(12分)解方程.
(1)3x(x-2)=x-2.
(2)4x2–8x+1=0
19.
(12分)
(1)计算:
(2)已知a=+2,b=-2,求下列代数式的值:
?ab2+ba2;?
a2-b2.
20.(8分)将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入.图2是它的平面示意图,AP=
6
cm,请根据图中的信息,求出容器中牛奶的高度.
21.(9分)如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始,沿AB边向点B以1
cm/s的速度移动,点Q从点B开始,沿BC边向点C以2
cm/s的速度移动,如果P、Q分别从A、B同时出发,运动多少秒后△PBQ的面积等于8
cm2.
22.(10分)如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
(1)求证:四边形AECD是菱形;
(2)若AB=6,BC=10,求EF的长.
23.(12分)(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,则有BE+DF=_______.若AB=2,则△CEF的周长为_______.?
(2)如图2,在四边形ABCD中,∠BAD=∠C=90°,AB=AD,点E,F分别在BC,CD上,且∠EAF=45°,试判断BE,EF,DF之间的数量关系,并说明理由.
24.(11分)如图(1),在正方形ABCD中,E,F分别为边AB,BC的中点,连接AF,DE交于点G.
(1)求证:AF⊥DE;
(2)如图(2),连接BG,BD,BD交AF于点H.
①求证:GB2=GA·GD;
②若AB=10,求三角形GBH的面积.
班级
姓名
考号
密
封
线
内
请
不
要
答
题
图
图(1)
图(2)
八年级数学期中检测卷(五四制专用)
(总分:150分
时间:120分钟)
一.选择题(共48分).
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
1.下列式子中,为最简二次根式的是( )
A.
B.
C.
D.
2.用配方法解一元二次方程x24x+1=0时,下列变形正确的是( )
A.(x2)2=1
B.(x2)2=5
C.(x+2)2=3
D.(x2)2=3
3.若方程x2-2x-4=0的两个实数根为α,β,则α2+β2的值为
(
)
A.12
B.10
C.4
D.-4
4.在下列各组根式中,是同类二次根式的是(
)
A.和
B.和
C.和
D.和
5.如图,在Rt△ABC中,∠BAC=90°,AB=6,点D是斜边BC的中点,若AD=5,则AC等于
( )
第5题图
第6题图
第7题图
6.菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A的纵坐标是1,则点B的坐标是( )
A.(3,1)
B.(3,-1)
C.(1,-3)
D.(1,3)
7.
如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,若AB=6,BC=9,则BF的长为( )
A.4
B.3
C.4.5
D.5
8.
如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2
m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高约为
( )
第8题图
第11题图
第14题图
A.5.5
m
B.6.2
m
C.11
m
D.2.2
m
9.
如图,在大小为4×4的正方形网格中,是相似三角形的是(
)
10.
如图,a,b,c在数轴上的位置如图所示,化简-|a+c|+的结果为(
)
A.2c-b
B.-b
C.b
D.-2a-b
11.
如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为
( )
A.2
B.4
C.6
D.8
12.若关于x的一元二次方程(k2)x22kx+k=6有实数根,则k的取值范围为( )
A.k0
B.k0且k≠2
C.k
D.k且k≠2
二.填空题(共28分).
13.
若是二次根式,则x的值可以为
(写出一个即可).
14.
如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条平行),剩余部分栽种花草,且栽种花草的面积77m2,设道路的宽为xm,则根据题意,可列方程为_______________.
15.
如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),
C(3,1),以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2∶1,则线段DF的长度为_______.
(
第15题图
第16题图
第17题图
16.
如图,在内有边长分别为a,b,c的三个正方形.则a、b、c满足的关系式是________
17.
如图,正方形ABCD和正方形CEFG的边长分别为a和b,正方形CEFG绕点C旋转.给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2.其中正确的结论是
(填写序号).?
三.解答题(共74分).
18.(12分)解方程.
(1)3x(x-2)=x-2.
(2)4x2–8x+1=0
19.
(12分)
(1)计算:
(2)已知a=+2,b=-2,求下列代数式的值:
?ab2+ba2;?
a2-b2.
20.(8分)将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入.图2是它的平面示意图,AP=
6
cm,请根据图中的信息,求出容器中牛奶的高度.
21.(9分)如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始,沿AB边向点B以1
cm/s的速度移动,点Q从点B开始,沿BC边向点C以2
cm/s的速度移动,如果P、Q分别从A、B同时出发,运动多少秒后△PBQ的面积等于8
cm2.
22.(10分)如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
(1)求证:四边形AECD是菱形;
(2)若AB=6,BC=10,求EF的长.
23.(12分)(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,则有BE+DF=_______.若AB=2,则△CEF的周长为_______.?
(2)如图2,在四边形ABCD中,∠BAD=∠C=90°,AB=AD,点E,F分别在BC,CD上,且∠EAF=45°,试判断BE,EF,DF之间的数量关系,并说明理由.
24.(11分)如图(1),在正方形ABCD中,E,F分别为边AB,BC的中点,连接AF,DE交于点G.
(1)求证:AF⊥DE;
(2)如图(2),连接BG,BD,BD交AF于点H.
①求证:GB2=GA·GD;
②若AB=10,求三角形GBH的面积.
班级
姓名
考号
密
封
线
内
请
不
要
答
题
图
图(1)
图(2)
同课章节目录
