冀教版八年级下册数学 第十九章平面直角坐标系达标检测卷(word版含答案)
文档属性
| 名称 | 冀教版八年级下册数学 第十九章平面直角坐标系达标检测卷(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 471.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 00:00:00 | ||
图片预览



文档简介
第十九章达标检测卷
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.如果座位表上“5列2行”记作(5,2),那么(4,3)表示( )
A.3列5行 B.5列3行
C.4列3行 D.3列4行
2.在平面直角坐标系中,若点P的坐标为(-3,2),则点P所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.点A的位置如图所示,则关于点A的位置,下列说法正确的是( )
A.距点O 4 km处
B.北偏东40°方向上4 km处
C.在点O北偏东50°方向上4 km处
D.在点O北偏东40°方向上4 km处
4.点P在平面直角坐标系的第二象限,P到x轴的距离为1,到y轴的距离为2,则点P的坐标是( )
A.(-1,2) B.(-2,1)
C.(1,-2) D.(2,-1)
5.点P(-2,3)关于x轴对称的点的坐标是( )
A.(-3,2) B.(2,-3)
C.(-2,-3) D.(2,3)
6.已知点P(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(-2,0) B.(0,-2)
C.(1,0) D.(0,1)
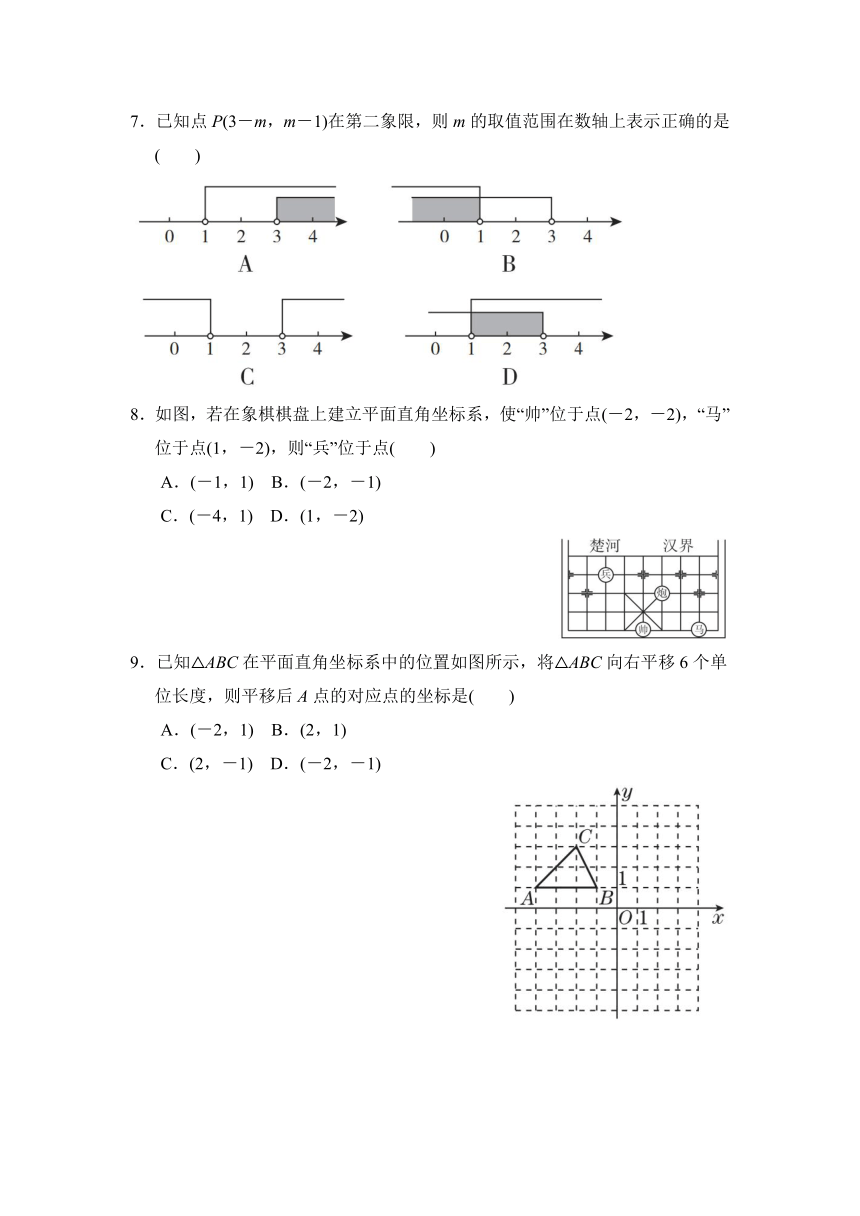
7.已知点P(3-m,m-1)在第二象限,则m的取值范围在数轴上表示正确的是( )
8.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-2,-2),“马”位于点(1,-2),则“兵”位于点( )
A.(-1,1) B.(-2,-1)
C.(-4,1) D.(1,-2)
9.已知△ABC在平面直角坐标系中的位置如图所示,将△ABC向右平移6个单位长度,则平移后A点的对应点的坐标是( )
A.(-2,1) B.(2,1)
C.(2,-1) D.(-2,-1)
10.如图是医院、公园和超市的平面示意图,超市在医院的南偏东25°的方向上,且到医院的距离为300 m,公园到医院的距离为400 m.若公园到超市的距离为500 m,则公园在医院的( )
A.北偏东75°的方向上
B.北偏东65°的方向上
C.北偏东55°的方向上
D.无法确定
11.如图,长方形ABCD的长为8,宽为4,分别以两组对边中点的连线为坐标轴建立平面直角坐标系,下列哪个点不在长方形上( )
A.(4,-2)
B.(-2,4)
C.(4,2)
D.(0,-2)
12.在平面直角坐标系xOy中,如果点A的坐标为(-3,3),点B的坐标为(2,0),那么三角形ABO的面积是( )
A.15 B.7.5 C.6 D.3
13.已知点M(1,-2),N(-3,-2),则直线MN与x轴、y轴的位置关系分别为( )
A.相交、相交 B.平行、平行
C.垂直、平行 D.平行、垂直
14.在平面直角坐标系中,将一个四边形各顶点的横、纵坐标都乘2,所得图形与原图形相比,下列说法正确的是( )
A.所得图形相当于将原图形横向拉长为原来的2倍,纵向不变
B.所得图形相当于将原图形纵向拉长为原来的2倍,横向不变
C.所得图形形状不变,面积扩大为原来的4倍
D.所得图形形状不变,面积扩大为原来的2倍
15.若某四边形各顶点的横坐标分别变为原来的相反数,纵坐标不变,所得图形与原图形位置相同,则这个四边形不可能是( )
A.长方形 B.直角梯形
C.正方形 D.等腰梯形
16.如图,已知正方形ABCD,顶点A(1,3),B(1,1),C(3,1),规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位长度”为一次变换,按这样操作,连续经过2 022次变换后,正方形ABCD的对角线交点M的坐标变为( )
A.(-2 020,2) B.(-2 020,-2)
C.(-2 021,-2) D.(-2 021,2)
二、填空题(每题3分,共9分)
17.在平面直角坐标系内,点M(a,1-a)一定不在第________象限.
18.已知A(a,-3),B(1,b),线段AB∥x轴,且AB=3.若a<1,则a+b=________.
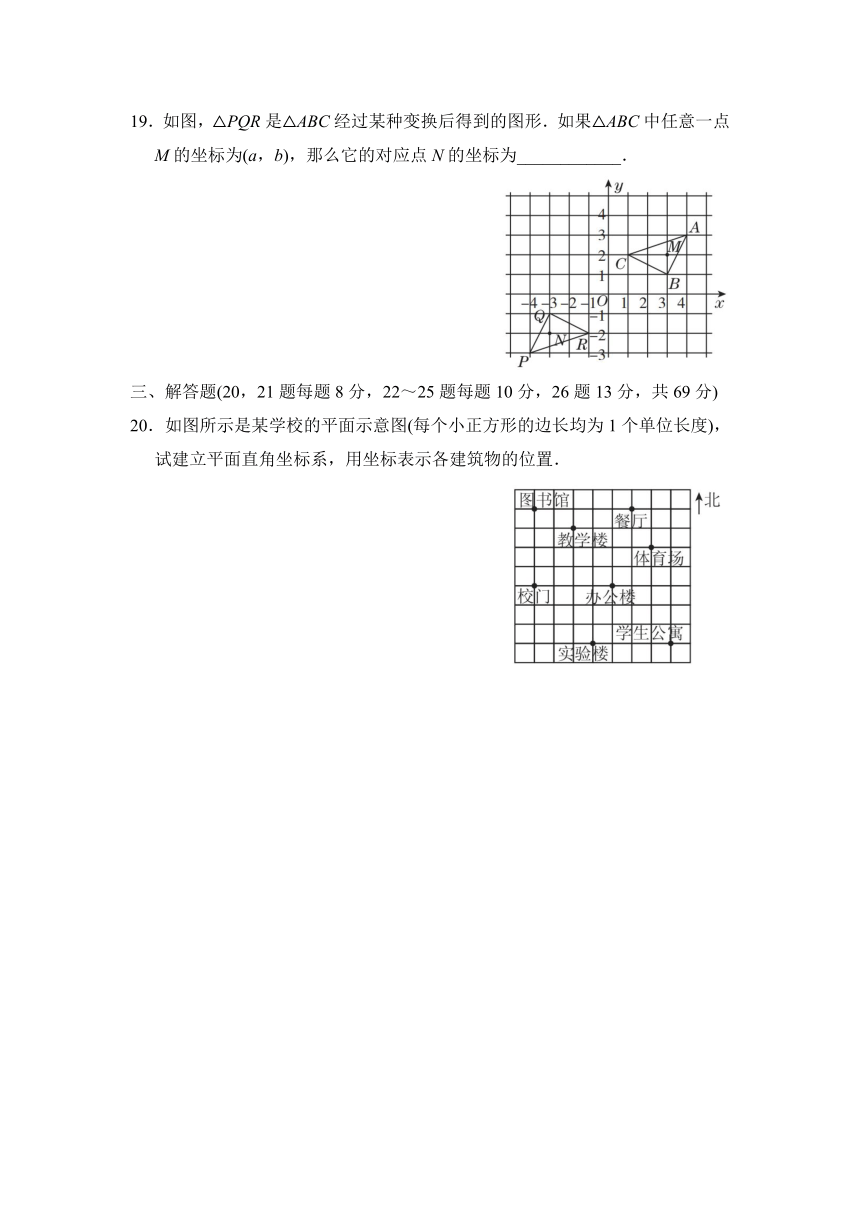
19.如图,△PQR是△ABC经过某种变换后得到的图形.如果△ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标为____________.
三、解答题(20,21题每题8分,22~25题每题10分,26题13分,共69分)
20.如图所示是某学校的平面示意图(每个小正方形的边长均为1个单位长度),试建立平面直角坐标系,用坐标表示各建筑物的位置.
21.在如图所示的平面直角坐标系中,描出点A(-2,1),B(-2,-2),C(2,-2),D(2,3),顺次连接各点,你能得到什么图形?先将该图形向上平移2个单位长度,再向右平移1个单位长度,作出平移后的图形,并求出平移后的图形的面积S.(每个小正方形的边长均为1个单位长度)
22.在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)分别写出△ABC各个顶点的坐标;
(2)分别写出顶点A关于x轴对称的点A′的坐标、顶点B关于y轴对称的点B′的坐标及顶点C关于原点对称的点C′的坐标;
(3)求线段BC的长.
23.如图,在平面直角坐标系中,O,A,B,C的坐标分别为(0,0),(-1,2),(-3,3)和(-2,1).
(1)若图中的各个点的纵坐标不变,横坐标都乘-1,与原图形相比,所得图形有什么变化?画出图形并说明一下变化.
(2)若图中的各个点的横坐标不变,纵坐标都乘-1,与原图形相比,所得图形有什么变化?画出图形并说明一下变化.
24.如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D、点B与点E、点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D、点B与点E、点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a,b的值.
25.在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.如图,已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.
(1)当m=3时,求点B的横坐标的所有可能值;
(2)当点B的横坐标为4n(n为正整数)时,用含n的代数式表示m.
26.如图①,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC?若存在这样一点,求出点Q的坐标;若不存在,试说明理由.
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),给出下列结论:①的值不变,②的值不变.其中有且只有一个是正确的,请你找出这个结论并求其值.
答案
一、1.C 2.B 3.D 4.B 5.C
6.B 点拨:本题运用方程思想.因为P(m+3,2m+4)在y轴上,所以点P的横坐标为0,即m+3=0,解得m=-3,故点P的坐标为(0,-2).
7.A
8.C 点拨:由“帅”与“马”的位置可以确定平面直角坐标系,进而可知“兵”位于点(-4,1),故选C.
9.B 10.B 11.B
12.D 点拨:此题首先运用数形结合思想,在平面直角坐标系中描点连线画出三角形ABO,然后运用转化思想将点的坐标转化为线段的长度,底BO=2,高为3,所以三角形ABO的面积=×2×3=3.
13.D
14.C 点拨:图形上各点的横、纵坐标都乘2,说明图形被横向、纵向分别拉长为原来的2倍,其形状不变,只是面积扩大为原来的4倍.
15.B 16.A
二、17.三 点拨:当a<0时,1-a>0.
18.-5
19.(-a,-b) 点拨:本题运用数形结合思想.通过观察可知点N与点M关于原点O对称.
三、20.解:如图所示,以办公楼所在位置为坐标原点,正东方向为x轴正方向、正北方向为y轴正方向建立平面直角坐标系,用坐标表示各建筑物的位置分别为办公楼(0,0),校门(-4,0),图书馆(-4,4),教学楼(-2,3),实验楼(-1,-3),餐厅(1,4),体育场(2,2),学生公寓(3,-3).
点拨:建立的坐标系不同,结果也会不同.
21.解:如图,得到直角梯形ABCD,平移后的图形为直角梯形A′B′C′D′;平移后的图形的面积S=(A′B′+D′C′)×B′C′=×(3+5)×4=16.
22.解:(1)A(-4,3),C(-2,5),B(3,0).
(2)点A′的坐标为(-4,-3),
点B′的坐标为(-3,0),
点C′的坐标为(2,-5).
(3)线段BC的长为=5 .
23.解:(1)各个点的纵坐标不变,横坐标都乘-1,得到新的坐标分别为(0,0),(1,2),(3,3),(2,1).
在坐标系中描出各点,再连接各点,如图所示.所得图形与原图形关于y轴对称.
(2)各个点的横坐标不变,纵坐标都乘-1,得到新的坐标分别为(0,0),(-1,-2),(-3,-3),(-2,-1).
在坐标系中描出各点,再连接各点,如图所示.所得图形与原图形关于x轴对称.
24.解:(1)A(2,3)与D(-2,-3),
B(1,2)与E(-1,-2),
C(3,1)与F(-3,-1);
对应点的坐标的特征:横坐标互为相反数,纵坐标互为相反数.
(2)由(1)可得a+3=-2a,4-b=-(2b-3),解得a=-1,b=-1.
25.解:(1)如图①,当点B的横坐标为3或4时,m=3,即当m=3时,点B的横坐标的所有可能值是3和4.
(2)如图②,
当点B的横坐标为4n=4时,
n=1,m=3;
当点B的横坐标为4n=8时,
n=2,m=9;
当点B的横坐标为4n=12时,
n=3,m=15,…,
当点B的横坐标为4n(n为正整数)时,
m=6n-3.
26.解:(1)C(0,2),D(4,2),
S四边形ABDC=8.
(2)存在.
设点Q到AB的距离为h,
S△QAB=×AB×h=2h,
由S△QAB=S四边形ABDC,
得2h=8,解得h=4,
∴点Q的坐标为(0,4)或(0,-4).
(3)结论①正确,如图,
过P点作PE∥AB交OC于E点,
则AB∥PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠DCP+∠BOP=∠CPE+∠OPE=∠CPO,
∴=1.
点拨:第(2)问易丢解,注意线段长转化为点的坐标时,要进行分类,体现了分类讨论思想的应用;第(3)问的技巧是分解图形法,把题目已知条件中涉及的几何条件从平面直角坐标系中分离出来,将问题转化为常见的求角度之间的数量关系来解决.
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.如果座位表上“5列2行”记作(5,2),那么(4,3)表示( )
A.3列5行 B.5列3行
C.4列3行 D.3列4行
2.在平面直角坐标系中,若点P的坐标为(-3,2),则点P所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.点A的位置如图所示,则关于点A的位置,下列说法正确的是( )
A.距点O 4 km处
B.北偏东40°方向上4 km处
C.在点O北偏东50°方向上4 km处
D.在点O北偏东40°方向上4 km处
4.点P在平面直角坐标系的第二象限,P到x轴的距离为1,到y轴的距离为2,则点P的坐标是( )
A.(-1,2) B.(-2,1)
C.(1,-2) D.(2,-1)
5.点P(-2,3)关于x轴对称的点的坐标是( )
A.(-3,2) B.(2,-3)
C.(-2,-3) D.(2,3)
6.已知点P(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(-2,0) B.(0,-2)
C.(1,0) D.(0,1)
7.已知点P(3-m,m-1)在第二象限,则m的取值范围在数轴上表示正确的是( )
8.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-2,-2),“马”位于点(1,-2),则“兵”位于点( )
A.(-1,1) B.(-2,-1)
C.(-4,1) D.(1,-2)
9.已知△ABC在平面直角坐标系中的位置如图所示,将△ABC向右平移6个单位长度,则平移后A点的对应点的坐标是( )
A.(-2,1) B.(2,1)
C.(2,-1) D.(-2,-1)
10.如图是医院、公园和超市的平面示意图,超市在医院的南偏东25°的方向上,且到医院的距离为300 m,公园到医院的距离为400 m.若公园到超市的距离为500 m,则公园在医院的( )
A.北偏东75°的方向上
B.北偏东65°的方向上
C.北偏东55°的方向上
D.无法确定
11.如图,长方形ABCD的长为8,宽为4,分别以两组对边中点的连线为坐标轴建立平面直角坐标系,下列哪个点不在长方形上( )
A.(4,-2)
B.(-2,4)
C.(4,2)
D.(0,-2)
12.在平面直角坐标系xOy中,如果点A的坐标为(-3,3),点B的坐标为(2,0),那么三角形ABO的面积是( )
A.15 B.7.5 C.6 D.3
13.已知点M(1,-2),N(-3,-2),则直线MN与x轴、y轴的位置关系分别为( )
A.相交、相交 B.平行、平行
C.垂直、平行 D.平行、垂直
14.在平面直角坐标系中,将一个四边形各顶点的横、纵坐标都乘2,所得图形与原图形相比,下列说法正确的是( )
A.所得图形相当于将原图形横向拉长为原来的2倍,纵向不变
B.所得图形相当于将原图形纵向拉长为原来的2倍,横向不变
C.所得图形形状不变,面积扩大为原来的4倍
D.所得图形形状不变,面积扩大为原来的2倍
15.若某四边形各顶点的横坐标分别变为原来的相反数,纵坐标不变,所得图形与原图形位置相同,则这个四边形不可能是( )
A.长方形 B.直角梯形
C.正方形 D.等腰梯形
16.如图,已知正方形ABCD,顶点A(1,3),B(1,1),C(3,1),规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位长度”为一次变换,按这样操作,连续经过2 022次变换后,正方形ABCD的对角线交点M的坐标变为( )
A.(-2 020,2) B.(-2 020,-2)
C.(-2 021,-2) D.(-2 021,2)
二、填空题(每题3分,共9分)
17.在平面直角坐标系内,点M(a,1-a)一定不在第________象限.
18.已知A(a,-3),B(1,b),线段AB∥x轴,且AB=3.若a<1,则a+b=________.
19.如图,△PQR是△ABC经过某种变换后得到的图形.如果△ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标为____________.
三、解答题(20,21题每题8分,22~25题每题10分,26题13分,共69分)
20.如图所示是某学校的平面示意图(每个小正方形的边长均为1个单位长度),试建立平面直角坐标系,用坐标表示各建筑物的位置.
21.在如图所示的平面直角坐标系中,描出点A(-2,1),B(-2,-2),C(2,-2),D(2,3),顺次连接各点,你能得到什么图形?先将该图形向上平移2个单位长度,再向右平移1个单位长度,作出平移后的图形,并求出平移后的图形的面积S.(每个小正方形的边长均为1个单位长度)
22.在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)分别写出△ABC各个顶点的坐标;
(2)分别写出顶点A关于x轴对称的点A′的坐标、顶点B关于y轴对称的点B′的坐标及顶点C关于原点对称的点C′的坐标;
(3)求线段BC的长.
23.如图,在平面直角坐标系中,O,A,B,C的坐标分别为(0,0),(-1,2),(-3,3)和(-2,1).
(1)若图中的各个点的纵坐标不变,横坐标都乘-1,与原图形相比,所得图形有什么变化?画出图形并说明一下变化.
(2)若图中的各个点的横坐标不变,纵坐标都乘-1,与原图形相比,所得图形有什么变化?画出图形并说明一下变化.
24.如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D、点B与点E、点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D、点B与点E、点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a,b的值.
25.在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.如图,已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.
(1)当m=3时,求点B的横坐标的所有可能值;
(2)当点B的横坐标为4n(n为正整数)时,用含n的代数式表示m.
26.如图①,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC?若存在这样一点,求出点Q的坐标;若不存在,试说明理由.
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),给出下列结论:①的值不变,②的值不变.其中有且只有一个是正确的,请你找出这个结论并求其值.
答案
一、1.C 2.B 3.D 4.B 5.C
6.B 点拨:本题运用方程思想.因为P(m+3,2m+4)在y轴上,所以点P的横坐标为0,即m+3=0,解得m=-3,故点P的坐标为(0,-2).
7.A
8.C 点拨:由“帅”与“马”的位置可以确定平面直角坐标系,进而可知“兵”位于点(-4,1),故选C.
9.B 10.B 11.B
12.D 点拨:此题首先运用数形结合思想,在平面直角坐标系中描点连线画出三角形ABO,然后运用转化思想将点的坐标转化为线段的长度,底BO=2,高为3,所以三角形ABO的面积=×2×3=3.
13.D
14.C 点拨:图形上各点的横、纵坐标都乘2,说明图形被横向、纵向分别拉长为原来的2倍,其形状不变,只是面积扩大为原来的4倍.
15.B 16.A
二、17.三 点拨:当a<0时,1-a>0.
18.-5
19.(-a,-b) 点拨:本题运用数形结合思想.通过观察可知点N与点M关于原点O对称.
三、20.解:如图所示,以办公楼所在位置为坐标原点,正东方向为x轴正方向、正北方向为y轴正方向建立平面直角坐标系,用坐标表示各建筑物的位置分别为办公楼(0,0),校门(-4,0),图书馆(-4,4),教学楼(-2,3),实验楼(-1,-3),餐厅(1,4),体育场(2,2),学生公寓(3,-3).
点拨:建立的坐标系不同,结果也会不同.
21.解:如图,得到直角梯形ABCD,平移后的图形为直角梯形A′B′C′D′;平移后的图形的面积S=(A′B′+D′C′)×B′C′=×(3+5)×4=16.
22.解:(1)A(-4,3),C(-2,5),B(3,0).
(2)点A′的坐标为(-4,-3),
点B′的坐标为(-3,0),
点C′的坐标为(2,-5).
(3)线段BC的长为=5 .
23.解:(1)各个点的纵坐标不变,横坐标都乘-1,得到新的坐标分别为(0,0),(1,2),(3,3),(2,1).
在坐标系中描出各点,再连接各点,如图所示.所得图形与原图形关于y轴对称.
(2)各个点的横坐标不变,纵坐标都乘-1,得到新的坐标分别为(0,0),(-1,-2),(-3,-3),(-2,-1).
在坐标系中描出各点,再连接各点,如图所示.所得图形与原图形关于x轴对称.
24.解:(1)A(2,3)与D(-2,-3),
B(1,2)与E(-1,-2),
C(3,1)与F(-3,-1);
对应点的坐标的特征:横坐标互为相反数,纵坐标互为相反数.
(2)由(1)可得a+3=-2a,4-b=-(2b-3),解得a=-1,b=-1.
25.解:(1)如图①,当点B的横坐标为3或4时,m=3,即当m=3时,点B的横坐标的所有可能值是3和4.
(2)如图②,
当点B的横坐标为4n=4时,
n=1,m=3;
当点B的横坐标为4n=8时,
n=2,m=9;
当点B的横坐标为4n=12时,
n=3,m=15,…,
当点B的横坐标为4n(n为正整数)时,
m=6n-3.
26.解:(1)C(0,2),D(4,2),
S四边形ABDC=8.
(2)存在.
设点Q到AB的距离为h,
S△QAB=×AB×h=2h,
由S△QAB=S四边形ABDC,
得2h=8,解得h=4,
∴点Q的坐标为(0,4)或(0,-4).
(3)结论①正确,如图,
过P点作PE∥AB交OC于E点,
则AB∥PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠DCP+∠BOP=∠CPE+∠OPE=∠CPO,
∴=1.
点拨:第(2)问易丢解,注意线段长转化为点的坐标时,要进行分类,体现了分类讨论思想的应用;第(3)问的技巧是分解图形法,把题目已知条件中涉及的几何条件从平面直角坐标系中分离出来,将问题转化为常见的求角度之间的数量关系来解决.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
