勾股定理及其逆定理复习课件

(共21张PPT)
初二 数学组
勾股定理及逆定理复习
复习目标
1.通过复习巩固勾股定理及其逆定理的内容及应用。
2.掌握勾股定理及其逆定理的内容，会利用勾股定理及其逆定解决实际问题。
3. 以极度的热情、全力以赴投入学习，享受合作学习的快乐。
重点：勾股定理及逆定理的应用
难点：灵活运用勾股定理及逆定理解决实际问题
课前复习情况展示
本次复习学案主要探究勾股定理及逆定理的应用，同学们
积极探讨，质量较高，呈现出一批优秀学案：
优秀小组：find dream 一组 争锋断空四组
御风追梦三组 （+2分）
优秀个人：
（+2分）
进步生：
存在问题：
1、误认为第三边为斜边，没有分类讨论；
2、方程思想意识不够，忘记单位；
2、步骤不条理，思路不够清晰，卷面乱。
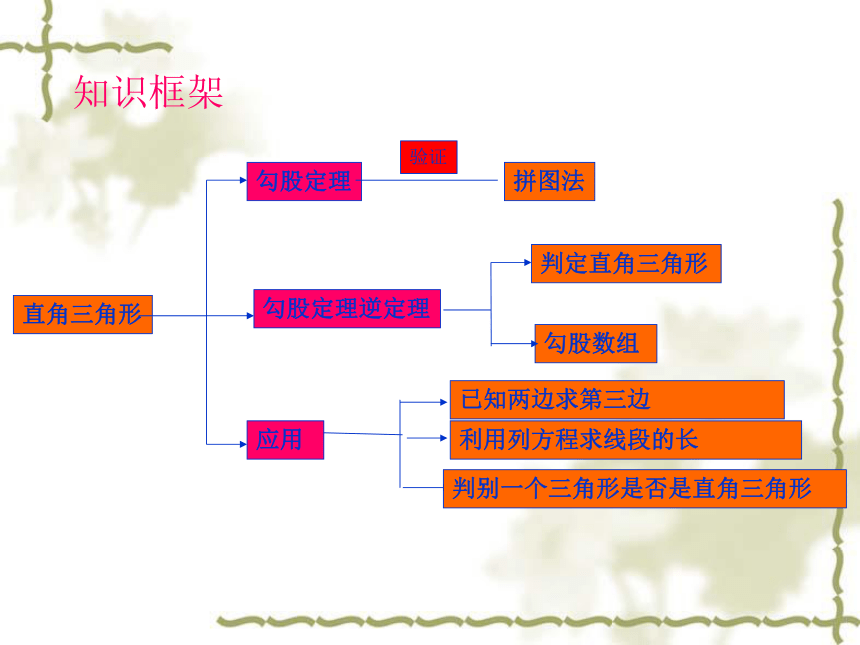
直角三角形
勾股定理
拼图法
验证
知识框架
勾股数组
勾股定理逆定理
判定直角三角形
应用
利用列方程求线段的长
已知两边求第三边
判别一个三角形是否是直角三角形
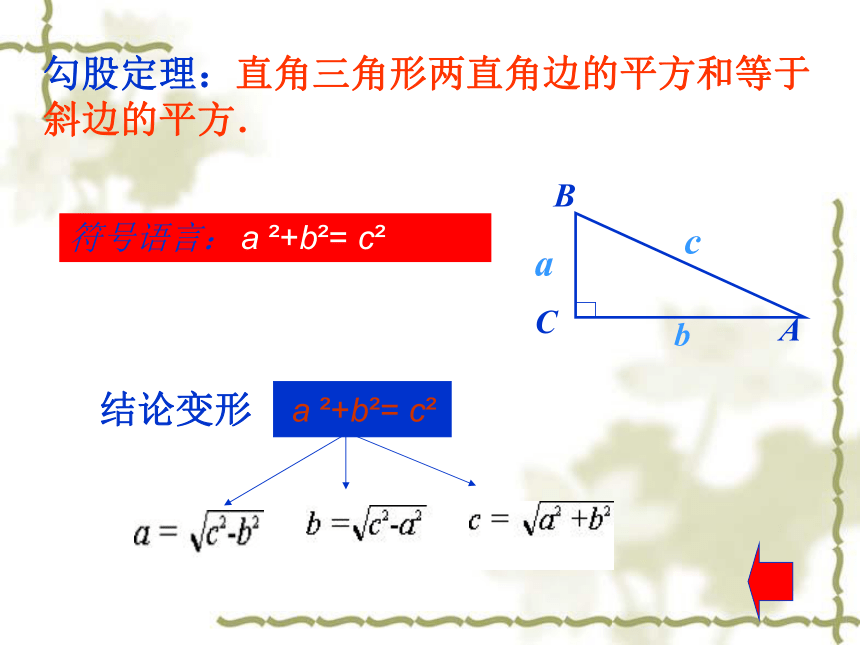
符号语言： a +b = c
a
b
c
A
B
C
勾股定理：直角三角形两直角边的平方和等于斜边的平方．
a +b = c
结论变形
判断技巧：最大边的平方=最小边的平方+中间边的平方.
勾股定理逆定理
如果三角形两边的平方等于第三边的平方，那么这个三角形是直角三角形.
1、△ABC三边长分别为7,24,25是判断△ ABC的形状
解：因为 7 +24 =25
所以 由勾股定理可知：三角形为直角三角形
具体要求：
1.重点讨论导学案例1,例2 例3；A、B层注重归纳总结勾股定理及其逆定理的常见题型及其解题方法；C层同学做好典题整理
2.先一对一讨论，再组内、组间讨论；
3. 明确每个题目考查的知识点，总结题目的规律、方法，注意规范做题步骤。
合作探究(8分钟)
明确目标：
A层学生要求在B层次的基础上培养创新意识,并拓展延伸,目标达成率120%。
B层同学熟练掌握基础知识，并能灵活运用知识解决问题 ,目标达成100%。
C层同学注重基础知识,掌握探究1-3,目标达成率80%。
高效展示
展示内容 展示小组
学案例1
学案例2
学案例3
要求：
⑴口头展示,声音洪亮、清楚;
书面展示要画图、步骤条理,
书写认真、规范。
⑵非展示同学整理落实案,
做好拓展。不浪费一分钟,
小组长做好安排和检查。
2组
3组
5组
点评内容 点评小组
学案例1
学案例2
学案例3
精彩点评
1组
6组
4组
要求：
⑴先点评对错；再点评思路方法，应该注意的问题,力争进行必要的变形拓展。
⑵其他同学认真倾听,积极思考,记好笔记,大胆质疑。
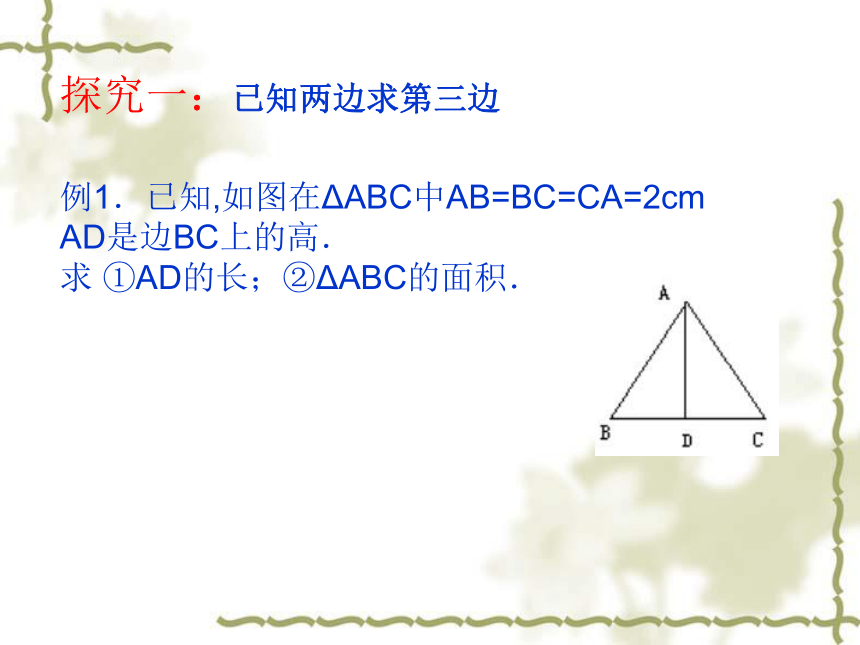
探究一：已知两边求第三边
例1．已知,如图在ΔABC中AB=BC=CA=2cm AD是边BC上的高．
求 ①AD的长；②ΔABC的面积．
1、已知直角三角形的两边分别是6,8，求斜边长_________
2.直角三角形的两条直角边分别是5cm,12cm,其斜边上的高是__________
8或10
分类思想
规律一：在直角三角形中，已知两边长求第三边,应分类讨论
例2．如图，铁路上A，B两点相距25km，C，D为两村庄，DA⊥AB于A，CB⊥AB于B，已知DA=15km，CB=10km，现在要在铁路AB上建一个土特产品收购站E，使得C，D两村到E站的距离相等，则E站应建在离A站多少km处？
探究点二：利用列方程求线段的长
A
D
E
B
C
方程思想
规律二：直角三角形中，当无法已知两边求第三边时,应采用间接法:灵活寻找题中的等量关系,利用勾股定理列方程。
例3、已知如图，四边形ABCD中，∠B=90°，AB=4， BC=3，CD=12，AD=13， 求这个四边形的面积
探究点三：判别一个三角形是否是直角三角形
_
A
_
B
_
C
_
D
已知如上图,四边形ABCD是实验中学一块空地的平面图，
其中∠B=90°,AB=4m, BC=3m，CD=12m，AD=13m，
现计划在这空地上植上草地绿化环境,若每平方米的草
皮需要150元，问需要投入资金多少元？
变
转化思想
规律三：在求不规则图形面积时，往往转化成规则图形如：三角形
规律小结
1、在运用勾股定理解决三角形问题时注意作高构造直角三角形
2 、在直角三角形中,已知两边长求斜边,应分类讨论
3、当已知条件中没有给出图形时,应图形结合,避免遗漏另一种情况。
4、直角三角形中,当无法已知两边求第三边时,应采用间接法,灵活 地寻找题中的等量关系,利用勾股定理列方程。
5、直角三角形两直角边的乘积等于斜边与斜边上的高的乘积
下图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了1米
旗杆有多高呢？
你能想个办法吗 请你与同桌交流设计方案
　　小明发现旗杆上的绳子垂到地面还多1米，当他们把绳子的下端拉开5米后，发现下端刚好接触地面，你能帮他们把旗杆的高度和绳子的长度计算出来吗？
A
B
C
５
x
x+1
学习了本节课,你有什么收获与困惑？
（同桌交流1分钟）
积跬步，行千里
方程思想
分类讨论思想
数形结合思想
转化思想
勾股定理应用
勾股数组
逆定理应用
收获
勾股定理及逆定理
知识方面
收获站
思想方法
要求：1、独立、自主、高效
2、认真审题,多角度思考，
规范步骤
3、时间5分钟
分层检测
A、层同学完成学案中的4、5、7
B、层同学完成学案中的4、5、6
C、层同学完成学案中的4、6
课堂评价
学科班长：1.回扣目标 总结收获
2.评出优秀小组和个人
分层作业
必做题 ：整理复习学案
选做题
1、课后提升案分层完成
2、A层同学负责引导C层同学 做好一帮一，组长检查落实