2020-2021学年人教版七年级数学下册 9.1.2不等式的性质课件(21张)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册 9.1.2不等式的性质课件(21张) |  | |
| 格式 | ppt | ||
| 文件大小 | 966.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 18:00:11 | ||
图片预览





文档简介
(共21张PPT)
义务教育课程标准实验教科书
数学
七年级
下册
性质一:等式两边同时加上(或减去)同一个数或式子,结果仍相等。
性质二:等式两边同时乘同一个数(或除以一个不为0的数),结果仍相等。
若a=b,则:
若a=b,
则
等式的基本性质
a+c=b+c或a-c=b-c
a·c=b·c,或a÷c=b÷c
(c≠0)
等式的传递性
若a=b,b=c则
a=c
性质
1:
如何用数学语言描述上面的现象呢?
不等式的性质
不等式两边加上(或减去)同一个数(或式子),不等号的方向
;
如果
a>b,
那么
不变
a+c>b+c或a-c>b-c
性质1
性质
2:
10_
_6
12×4_
_6×4
12÷3_
_6÷3
(–8)
_
_4
(–8)×0.5_
_4×0.5
(–8)÷2_
_4÷2
观察:用“<”或“>”填空,并讨论其中的规律.
性质
3:
温馨提示:
乘以或除以的数都是什么数呢?
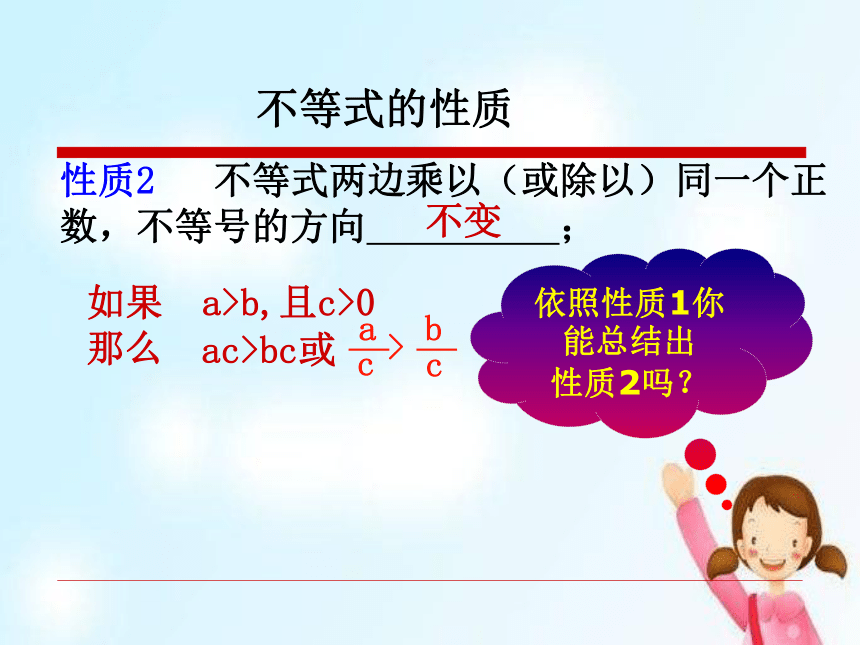
依照性质1你能总结出
性质2吗?
不等式的性质
不等式两边乘以(或除以)同一个正数,不等号的方向
;
如果
a>b,且c>0
那么
不变
ac>bc或
a
c
b
c
>
性质2
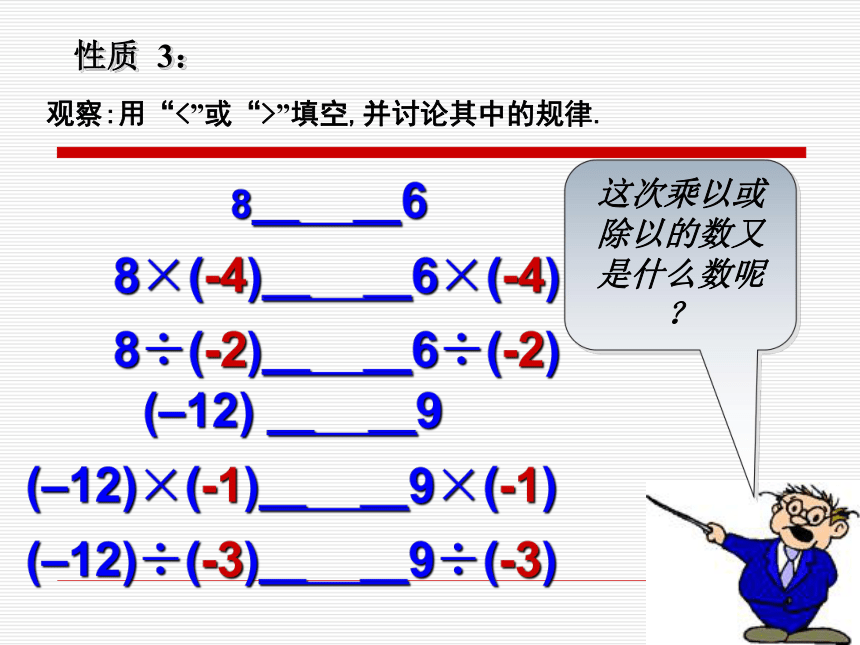
观察:用“<”或“>”填空,并讨论其中的规律.
性质
3:
8_
_6
8×(-4)_
_6×(-4)
8÷(-2)_
_6÷(-2)
(–12)
_
_9
(–12)×(-1)_
_9×(-1)
(–12)÷(-3)_
_9÷(-3)
这次乘以或除以的数又是什么数呢?
不等式的性质
不等式两边乘以(或除以)同一个负数,不等号的方向
;
如果
a>b,且c<0
那么
改变
aca
c
b
c
<
想一想:对于不等式a>b,当c=0时,ac
bc
性质3
不等式的传递性
若a>b,b>c则
a>c
不等式的性质
等式的性质
性质1
不等式两边加上(或减去)同一个数(或式子),不等号的方向不变;
性质2
不等式两边乘以(或除以)同一个正数,不等号的方向不变;
性质3
不等式两边乘以(或除以)同一个负数,不等号的方向改变。
不等式的传递性
性质1
等式两边同时加上(或减去)同一个数或式子,结果仍相等。
性质2
等式两边同时乘同一个(或除以一个不为0的)数,结果仍相等。
等式的传递性
数
相等
正数
方向不变
负数
方向改变
如果a>b,那么
(1)a-3
b-3(性质
)
(2)2a
2b(性质
)
(3)-3a
-3b(性质
)
(4)a-b
0(性质
)
(5)-4a+1
-4b+1(性质
)
利用不等式的性质填空
(
)
判断正误
(
)
(
)
(
)
(
)
(1)若x+3>-6,两边同减去3,得__
__
,依据_
___
.
(2)若-0.5x≤4,两边同乘以-2,得__
_
,依据__
_
.
选择适当的不等号填空:
x
>-9
性质1
X≥-8
性质3
性质3
(4)若3x+8<2,两边同减去8,得_
_,依据__
___
,
两边再同时除以3,得__
__
_,依据__
___
.
3x
<-6
性质1
x
<-3
性质2
例1:利用不等式的性质解下列不等式并把解集表示在数轴上
(1)3x<
2x+1
(2)x-7>26
(3)
分析:解不等式,就是要借助不等式的性质使不等式逐步化为x>a或x什么是解不等式呢?
(4)-4x≥12
(1)3x<
2x+1
例
1
解(1)根据不等式的性质1,不等式两边减2x,不等式的方向不变,得
1
(4)-4x≥12
解:根据不等式性质3,不等式两边除以-4,不等式方向改变,得
-4x÷(-4)
≤12÷(-4)
x
≤
-3
(3)
解:根据不等式性质2,不等式两边乘
,不等式方向不变,得
(2)x-7>26
解:根据不等式性质1,不等式两边加7,不等式方向不变,得
X-7+7>26+7
X>33
50
75
-3
75
33
(3)已知
a
<
-
1
,则下列不等式中错误的是(
)
A
4a
<
-
4
B
-a+2
>
3
C
a
+
2
<
1
D
-4a
<
4
(4)已知a>b,c为任意实数,则下列不等式总成立的是(
)
A
a-c>b-c
B
a+cC
acD
ac>bc
(2)已知x
<
y,下列哪个不等式成立(
)
A
-
5
x
<
-
5
y
B
x
–
3
<
y
–
3
C
-
3
x
+2
<
-
3
y
+
2
D
3
x
+
2
>
3y
+
2
(1)若a>b,则下列式子中一定成立的是(
)
A
a-3
<
b-3
B
-2a>-2b
C
a/4D
a>b+1
B
A
D
B
设A、B、C表示三种不同的物体,现用天平称了两次,情况如图所示,那么“A”、“B”、“C”这三个物体的质量按从大到小的顺序排列应为(
)
A.ABC
B.CBA
C.BAC
D.BCA
A
谈谈你这节课的收获。
P119
第1题、第2题
P120
第5、9题
义务教育课程标准实验教科书
数学
七年级
下册
性质一:等式两边同时加上(或减去)同一个数或式子,结果仍相等。
性质二:等式两边同时乘同一个数(或除以一个不为0的数),结果仍相等。
若a=b,则:
若a=b,
则
等式的基本性质
a+c=b+c或a-c=b-c
a·c=b·c,或a÷c=b÷c
(c≠0)
等式的传递性
若a=b,b=c则
a=c
性质
1:
如何用数学语言描述上面的现象呢?
不等式的性质
不等式两边加上(或减去)同一个数(或式子),不等号的方向
;
如果
a>b,
那么
不变
a+c>b+c或a-c>b-c
性质1
性质
2:
10_
_6
12×4_
_6×4
12÷3_
_6÷3
(–8)
_
_4
(–8)×0.5_
_4×0.5
(–8)÷2_
_4÷2
观察:用“<”或“>”填空,并讨论其中的规律.
性质
3:
温馨提示:
乘以或除以的数都是什么数呢?
依照性质1你能总结出
性质2吗?
不等式的性质
不等式两边乘以(或除以)同一个正数,不等号的方向
;
如果
a>b,且c>0
那么
不变
ac>bc或
a
c
b
c
>
性质2
观察:用“<”或“>”填空,并讨论其中的规律.
性质
3:
8_
_6
8×(-4)_
_6×(-4)
8÷(-2)_
_6÷(-2)
(–12)
_
_9
(–12)×(-1)_
_9×(-1)
(–12)÷(-3)_
_9÷(-3)
这次乘以或除以的数又是什么数呢?
不等式的性质
不等式两边乘以(或除以)同一个负数,不等号的方向
;
如果
a>b,且c<0
那么
改变
ac
c
b
c
<
想一想:对于不等式a>b,当c=0时,ac
bc
性质3
不等式的传递性
若a>b,b>c则
a>c
不等式的性质
等式的性质
性质1
不等式两边加上(或减去)同一个数(或式子),不等号的方向不变;
性质2
不等式两边乘以(或除以)同一个正数,不等号的方向不变;
性质3
不等式两边乘以(或除以)同一个负数,不等号的方向改变。
不等式的传递性
性质1
等式两边同时加上(或减去)同一个数或式子,结果仍相等。
性质2
等式两边同时乘同一个(或除以一个不为0的)数,结果仍相等。
等式的传递性
数
相等
正数
方向不变
负数
方向改变
如果a>b,那么
(1)a-3
b-3(性质
)
(2)2a
2b(性质
)
(3)-3a
-3b(性质
)
(4)a-b
0(性质
)
(5)-4a+1
-4b+1(性质
)
利用不等式的性质填空
(
)
判断正误
(
)
(
)
(
)
(
)
(1)若x+3>-6,两边同减去3,得__
__
,依据_
___
.
(2)若-0.5x≤4,两边同乘以-2,得__
_
,依据__
_
.
选择适当的不等号填空:
x
>-9
性质1
X≥-8
性质3
性质3
(4)若3x+8<2,两边同减去8,得_
_,依据__
___
,
两边再同时除以3,得__
__
_,依据__
___
.
3x
<-6
性质1
x
<-3
性质2
例1:利用不等式的性质解下列不等式并把解集表示在数轴上
(1)3x<
2x+1
(2)x-7>26
(3)
分析:解不等式,就是要借助不等式的性质使不等式逐步化为x>a或x
(4)-4x≥12
(1)3x<
2x+1
例
1
解(1)根据不等式的性质1,不等式两边减2x,不等式的方向不变,得
1
(4)-4x≥12
解:根据不等式性质3,不等式两边除以-4,不等式方向改变,得
-4x÷(-4)
≤12÷(-4)
x
≤
-3
(3)
解:根据不等式性质2,不等式两边乘
,不等式方向不变,得
(2)x-7>26
解:根据不等式性质1,不等式两边加7,不等式方向不变,得
X-7+7>26+7
X>33
50
75
-3
75
33
(3)已知
a
<
-
1
,则下列不等式中错误的是(
)
A
4a
<
-
4
B
-a+2
>
3
C
a
+
2
<
1
D
-4a
<
4
(4)已知a>b,c为任意实数,则下列不等式总成立的是(
)
A
a-c>b-c
B
a+c
ac
ac>bc
(2)已知x
<
y,下列哪个不等式成立(
)
A
-
5
x
<
-
5
y
B
x
–
3
<
y
–
3
C
-
3
x
+2
<
-
3
y
+
2
D
3
x
+
2
>
3y
+
2
(1)若a>b,则下列式子中一定成立的是(
)
A
a-3
<
b-3
B
-2a>-2b
C
a/4D
a>b+1
B
A
D
B
设A、B、C表示三种不同的物体,现用天平称了两次,情况如图所示,那么“A”、“B”、“C”这三个物体的质量按从大到小的顺序排列应为(
)
A.ABC
B.CBA
C.BAC
D.BCA
A
谈谈你这节课的收获。
P119
第1题、第2题
P120
第5、9题
