2020—2021学年苏科版七年级下册数学课件 10.3解二元一次方程组(31张)
文档属性
| 名称 | 2020—2021学年苏科版七年级下册数学课件 10.3解二元一次方程组(31张) |  | |
| 格式 | ppt | ||
| 文件大小 | 826.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 11:28:17 | ||
图片预览











文档简介
(共31张PPT)
解二元一次方程组(1)
问题1:什么是二元一次方程?
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
问题2:有那位同学能举出生活中运用二元一次方程组解决问题的例子。并根据题意列出方程。
回顾与思考
李明和妈妈买了18元的苹果和梨共5千克,1千克苹果售价4元,1千克梨售价3元,李明和妈妈买苹果和梨各多少千克?
列方程组为{
x+y=5
4x+3y=18
考考你
(1)苹果的重量+梨的重量=5
(2)苹果的总价+梨的总价=18
设买苹果x千克,买梨y千克。
分析:
由①
,得y=5-x。
③
由于方程组中相同的字母表示同一个未知数,所以方程②中的y也等于5-x,可以用5-x代替方程②中的y。这样就有4x+3(5-x)=18
④
李明和妈妈到底买了多少苹果,多少梨?要知道这个问题,我们就要想一想二元一次方程组
2
1
4x+3y=18
x+y=5
怎样解?
考考你
这样,我们就得到二元一次方程组
的解
x+y=5
4x+3y=18
x=3
y=2
因此,李明和妈妈共买了苹果3千克,梨2千克。
解所得的一元一次方程④
,得x=3
再把x=3代入③,
得y=2
例1:解方程组
3x+2y=14
①
X=y+3
②
所以原方程组的解是
x=4
y=1
要在实践中学习哟
解:将②代入①
,得3(y+3)+2y=14
3y+9+2y=14
5y=5
y=1
将y=1代入②,得
x=4
把求出的解代入
原方程组,可以知
道你解得对不对。
①
②
分析:①式
中的y就是
12-x.
解:由①得
y=12-x
.
③
将③代入②,得2x+12-x=20
解这个一元一次方程,得
x=8
将x=8代入③,得
y=4
.
所以原方程组的解是
本题能否通过消去x解这个方程组吗?
y=2x
①
X+y=12
②
1.
2.
x+y=11
①
X
-
y=7
②
解下列方程组
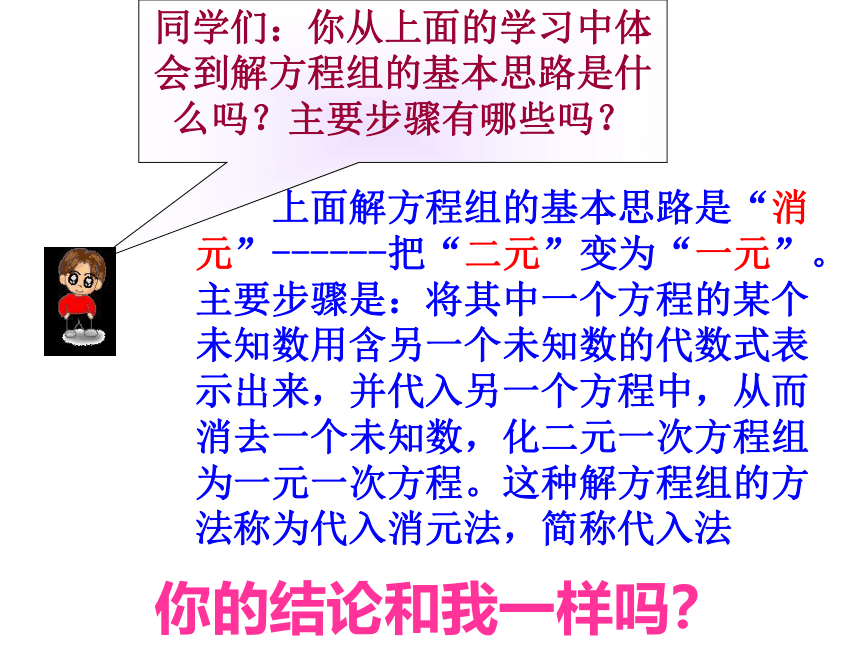
上面解方程组的基本思路是“消元”------把“二元”变为“一元”。主要步骤是:将其中一个方程的某个未知数用含另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。这种解方程组的方法称为代入消元法,简称代入法
你的结论和我一样吗?
同学们:你从上面的学习中体会到解方程组的基本思路是什么吗?主要步骤有哪些吗?
解二元一次方程组
⑴
x+y=5
①
x-y=1
②
⑵
2x+3y=40
①
x
-y=-5
②
2、已知(2x+3y-4)+∣x+3y-7∣=0
则x=
,y=
。
2
-3
—
10
3
随堂练习:
y=2x
⑴
x+y=12
⑵
x=—
y-5
2
4x+3y=65
⑶
x+y=11
x-y=7
⑷
3x-2y=9
x+2y=3
x=4
y=8
x=5
y=15
x=9
y=2
x=3
y=0
你解对了吗?
同学们:你能把我们今天学习的内容小结一下吗?
1、
本节课我们知道了用代入消元法解二元一次方程组的基本思路是“消元”。即把“二元”化为“一元”,化二元一次方程组为一元一次方程。
2、
把求出的解代入原方程组,可以检验解题过程是否正确。
课堂检测:
2.一个长方形的长是宽的3倍,如果长减少3
cm
,宽增加4cm
,这个长方形就变成了一个正方形.求这个长方形的长和宽.
3.如果一个两位数加上45,恰好等于把这个两位数的个位数字与十位数字对调后组成的新两位数.这个两位数的十位数字和个位数字的和是7
,你能知道这个两位数吗?
教后记:
想来学生在未学之前就有相当一部分同学对此很感兴趣并进行了研究,注意本节课的解二元一次方程组的解题思想为“代入消元”,它的适用范围也很清楚:最好是某个未知数的前面的系数的绝对值为1,否则尽量避免使用这种方法。再者注意变形的等价性,代入要细心,计算后要检验。课件的容量过大时,分组进行板演,注意准确率的同时要加快解题速度。
解二元一次方程组(2)
问题2:代入消元法解二元一次方程组
的一般步骤是什么?
问题1:解方程组的基本思路是什么?
把“二元”变为“一元”
回顾与思考
列方程组为{
3x+2y=23
5x+2y=33
考考你
(1)3瓶苹果汁的售价+
2瓶橙汁的售价=23
(2)5瓶苹果汁的售价+
2瓶橙汁的售价=33
解:设每瓶苹果汁是x元每瓶橙汁售价是y元.
分析:
买3瓶苹果汁和2瓶橙汁共需23元,买5瓶苹果汁和2瓶橙汁共需33元,每瓶苹果汁和每瓶橙汁售价各是多少?
3x+2y=23
5x+2y=33
{
②
①
解:
②-
①,得
2x=10
x=5
把x=5代入①,得
3×5+2y=23
解这个方程得
y=4
所以原方程组的解是
{
x=5
y=4
例1:解方程组
x+2y=1
①
3X-2y=5
②
解:
①+
②
,得
4x=6
x=
将x=
代入①,得
+2y=1
解这个方程得
y=
所以原方程组的解是
x=
y=
解这个方程得
2x+y=32
①
2X-y=0
②
1.
2.
7x+3y=11
①
2X
-
3y=7
②
解下列方程组:
解:
①×3,
得
15x-6y=12
③
②×2,得
4x-6y=-10
④
③-④,得
11
x=22
解这个方程得
x=2
将x=2
代入①,得
5×2-2y=4
解这个方程得
y=3
所以原方程组的解是
例2:解方程组
5x-2y=4
①
2X-3y=-5
②
{
x=2
y=3
本题能否通过消去x解这个方程组?
5x-2y=4
①
2X-3y=-5
②
动手试一试
上面解方程组的基本思路还是“消元”------把“二元”变为“一元”。主要步骤是:把方程组的两个方程(或先作适当变形)相加或相减,消去其中一个未知数,把解二元一次方程组转化为解一元一次方程.这种解方程组的方法叫做加减消元法,简称加减法.
同学们:你从上面的学习中体会到解方程组的基本思路是什么吗?主要步骤有哪些吗?
1、解二元一次方程组
⑴
3x-2y=5
①
X+3y=9
②
⑵
6x+5y=25
①
3x
+4y=20
②
做一做
(3)
3s+4t=7
①
3t-2s=1
②
(4)
2x+3y=-1
①
4x
-9y=8
②
例3:解方程组
练一练
⑴
0.6x-0.5y=0.4
2X-3y=4
(2)
3X-4y=-7
(3)
X-2y=-1
⑴
0.6x-0.5y=0.4
2X-3y=4
(2)
3X-4y=-7
(3)
X-2y=-1
已知关于x,y的方程组
与
的解相同,求a,b的值.
ax+2by=4
X+y=1
x-y=3
bX+(a-1)y=3
已知关于x,y的方程组的解
满足x+y=4,求a的值.
3x+2y=a+2
2X+3y=2a
相信你能行
1.
2.
小结与回顾
1、
本节课我们知道了用加减消元法解二元一次方程组的基本思路是“消元”。即把“二元”化为“一元”,化二元一次方程组为一元一次方程。
2、用加减消元法解二元一次方程组的一般步骤.
3、把求出的解代入原方程组,可以检验解是否正确。
教后记:
这节课的主要教学目的使学生会用加减消元法解决比上节课稍微复杂二元一次方程组,通过本节课的教学实践,发现学生对于加减消元思想接受较快,但学生在这节课的学习后,很容易形成这样的习惯:不管什么类型的二元一次方程组他都想用“加减消元”,教者要注意把握,适时提醒,要注意引导学生思考这样一个问题:何时使用“加减消元”会更好?让学生讨论后得出结论!
解二元一次方程组(1)
问题1:什么是二元一次方程?
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
问题2:有那位同学能举出生活中运用二元一次方程组解决问题的例子。并根据题意列出方程。
回顾与思考
李明和妈妈买了18元的苹果和梨共5千克,1千克苹果售价4元,1千克梨售价3元,李明和妈妈买苹果和梨各多少千克?
列方程组为{
x+y=5
4x+3y=18
考考你
(1)苹果的重量+梨的重量=5
(2)苹果的总价+梨的总价=18
设买苹果x千克,买梨y千克。
分析:
由①
,得y=5-x。
③
由于方程组中相同的字母表示同一个未知数,所以方程②中的y也等于5-x,可以用5-x代替方程②中的y。这样就有4x+3(5-x)=18
④
李明和妈妈到底买了多少苹果,多少梨?要知道这个问题,我们就要想一想二元一次方程组
2
1
4x+3y=18
x+y=5
怎样解?
考考你
这样,我们就得到二元一次方程组
的解
x+y=5
4x+3y=18
x=3
y=2
因此,李明和妈妈共买了苹果3千克,梨2千克。
解所得的一元一次方程④
,得x=3
再把x=3代入③,
得y=2
例1:解方程组
3x+2y=14
①
X=y+3
②
所以原方程组的解是
x=4
y=1
要在实践中学习哟
解:将②代入①
,得3(y+3)+2y=14
3y+9+2y=14
5y=5
y=1
将y=1代入②,得
x=4
把求出的解代入
原方程组,可以知
道你解得对不对。
①
②
分析:①式
中的y就是
12-x.
解:由①得
y=12-x
.
③
将③代入②,得2x+12-x=20
解这个一元一次方程,得
x=8
将x=8代入③,得
y=4
.
所以原方程组的解是
本题能否通过消去x解这个方程组吗?
y=2x
①
X+y=12
②
1.
2.
x+y=11
①
X
-
y=7
②
解下列方程组
上面解方程组的基本思路是“消元”------把“二元”变为“一元”。主要步骤是:将其中一个方程的某个未知数用含另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程。这种解方程组的方法称为代入消元法,简称代入法
你的结论和我一样吗?
同学们:你从上面的学习中体会到解方程组的基本思路是什么吗?主要步骤有哪些吗?
解二元一次方程组
⑴
x+y=5
①
x-y=1
②
⑵
2x+3y=40
①
x
-y=-5
②
2、已知(2x+3y-4)+∣x+3y-7∣=0
则x=
,y=
。
2
-3
—
10
3
随堂练习:
y=2x
⑴
x+y=12
⑵
x=—
y-5
2
4x+3y=65
⑶
x+y=11
x-y=7
⑷
3x-2y=9
x+2y=3
x=4
y=8
x=5
y=15
x=9
y=2
x=3
y=0
你解对了吗?
同学们:你能把我们今天学习的内容小结一下吗?
1、
本节课我们知道了用代入消元法解二元一次方程组的基本思路是“消元”。即把“二元”化为“一元”,化二元一次方程组为一元一次方程。
2、
把求出的解代入原方程组,可以检验解题过程是否正确。
课堂检测:
2.一个长方形的长是宽的3倍,如果长减少3
cm
,宽增加4cm
,这个长方形就变成了一个正方形.求这个长方形的长和宽.
3.如果一个两位数加上45,恰好等于把这个两位数的个位数字与十位数字对调后组成的新两位数.这个两位数的十位数字和个位数字的和是7
,你能知道这个两位数吗?
教后记:
想来学生在未学之前就有相当一部分同学对此很感兴趣并进行了研究,注意本节课的解二元一次方程组的解题思想为“代入消元”,它的适用范围也很清楚:最好是某个未知数的前面的系数的绝对值为1,否则尽量避免使用这种方法。再者注意变形的等价性,代入要细心,计算后要检验。课件的容量过大时,分组进行板演,注意准确率的同时要加快解题速度。
解二元一次方程组(2)
问题2:代入消元法解二元一次方程组
的一般步骤是什么?
问题1:解方程组的基本思路是什么?
把“二元”变为“一元”
回顾与思考
列方程组为{
3x+2y=23
5x+2y=33
考考你
(1)3瓶苹果汁的售价+
2瓶橙汁的售价=23
(2)5瓶苹果汁的售价+
2瓶橙汁的售价=33
解:设每瓶苹果汁是x元每瓶橙汁售价是y元.
分析:
买3瓶苹果汁和2瓶橙汁共需23元,买5瓶苹果汁和2瓶橙汁共需33元,每瓶苹果汁和每瓶橙汁售价各是多少?
3x+2y=23
5x+2y=33
{
②
①
解:
②-
①,得
2x=10
x=5
把x=5代入①,得
3×5+2y=23
解这个方程得
y=4
所以原方程组的解是
{
x=5
y=4
例1:解方程组
x+2y=1
①
3X-2y=5
②
解:
①+
②
,得
4x=6
x=
将x=
代入①,得
+2y=1
解这个方程得
y=
所以原方程组的解是
x=
y=
解这个方程得
2x+y=32
①
2X-y=0
②
1.
2.
7x+3y=11
①
2X
-
3y=7
②
解下列方程组:
解:
①×3,
得
15x-6y=12
③
②×2,得
4x-6y=-10
④
③-④,得
11
x=22
解这个方程得
x=2
将x=2
代入①,得
5×2-2y=4
解这个方程得
y=3
所以原方程组的解是
例2:解方程组
5x-2y=4
①
2X-3y=-5
②
{
x=2
y=3
本题能否通过消去x解这个方程组?
5x-2y=4
①
2X-3y=-5
②
动手试一试
上面解方程组的基本思路还是“消元”------把“二元”变为“一元”。主要步骤是:把方程组的两个方程(或先作适当变形)相加或相减,消去其中一个未知数,把解二元一次方程组转化为解一元一次方程.这种解方程组的方法叫做加减消元法,简称加减法.
同学们:你从上面的学习中体会到解方程组的基本思路是什么吗?主要步骤有哪些吗?
1、解二元一次方程组
⑴
3x-2y=5
①
X+3y=9
②
⑵
6x+5y=25
①
3x
+4y=20
②
做一做
(3)
3s+4t=7
①
3t-2s=1
②
(4)
2x+3y=-1
①
4x
-9y=8
②
例3:解方程组
练一练
⑴
0.6x-0.5y=0.4
2X-3y=4
(2)
3X-4y=-7
(3)
X-2y=-1
⑴
0.6x-0.5y=0.4
2X-3y=4
(2)
3X-4y=-7
(3)
X-2y=-1
已知关于x,y的方程组
与
的解相同,求a,b的值.
ax+2by=4
X+y=1
x-y=3
bX+(a-1)y=3
已知关于x,y的方程组的解
满足x+y=4,求a的值.
3x+2y=a+2
2X+3y=2a
相信你能行
1.
2.
小结与回顾
1、
本节课我们知道了用加减消元法解二元一次方程组的基本思路是“消元”。即把“二元”化为“一元”,化二元一次方程组为一元一次方程。
2、用加减消元法解二元一次方程组的一般步骤.
3、把求出的解代入原方程组,可以检验解是否正确。
教后记:
这节课的主要教学目的使学生会用加减消元法解决比上节课稍微复杂二元一次方程组,通过本节课的教学实践,发现学生对于加减消元思想接受较快,但学生在这节课的学习后,很容易形成这样的习惯:不管什么类型的二元一次方程组他都想用“加减消元”,教者要注意把握,适时提醒,要注意引导学生思考这样一个问题:何时使用“加减消元”会更好?让学生讨论后得出结论!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
