2021年江苏省无锡蠡园中学九年级中考第一次适应考试数学试卷(word版无答案)
文档属性
| 名称 | 2021年江苏省无锡蠡园中学九年级中考第一次适应考试数学试卷(word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 190.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 15:13:11 | ||
图片预览

文档简介
2020-2021学年江苏省无锡蠡园中学九年级中考第一次适应考试
数学试卷
(考试时间:120分钟
试卷分值:130分)
一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是正确的,请把正确的选项填涂在答卷相应的位置.)
1、﹣4的相反数
( ▲ )
A.
B.4
C.﹣4
D.±4
2、下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( ▲ )
3、函数y=中自变量x的取值范围是
(▲)
A.x>2
B.x≥2
C.x≤2
D.x≠2
4、下列运算正确的是
( ▲ )
A.
B.
C.
D.
5、如图是由5个相同的正方体搭成的几何体,其左视图是
( ▲ )
6、为了调查某小区居民的用水情况,随机抽查了若干户家庭的月用水量,结果如下表:
月用水量(吨)
3
4
5
8
户数
2
3
4
1
则关于这若干户家庭的月用水量,下列说法中错误的是( ▲ )
A.调查了10户家庭的月用水量
B.平均数是4.6
C.众数是4
D.中位数是4.5
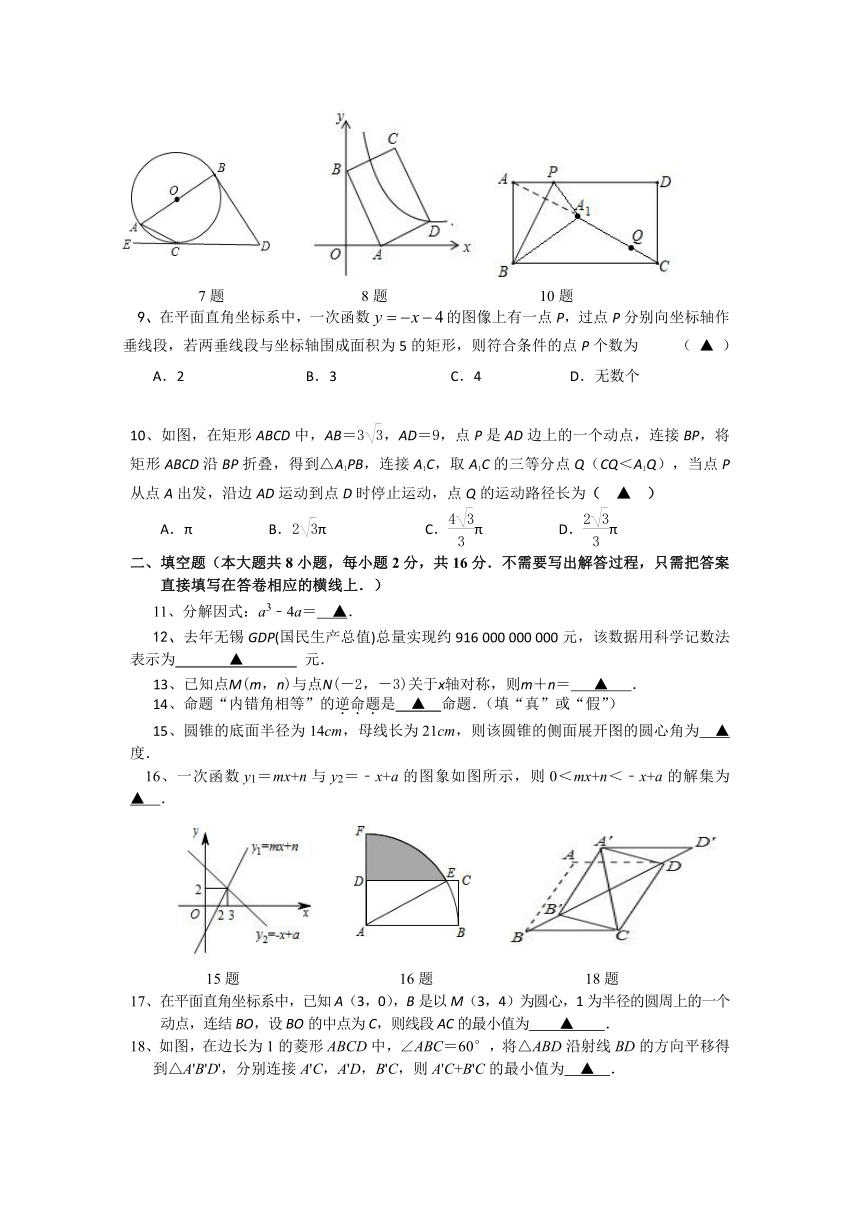
7、如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,
若∠ACE=25°,则∠D的度数是( ▲ )
A.50°
B.55°
C.60°
D.65°
8、如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0)、B(0,6)分别在x轴、y轴上,反比例函数的图象经过点D,则k值为( ▲ )
A.-14
B.14
C.7
D.-7
7题
8题
10题
9、在平面直角坐标系中,一次函数的图像上有一点P,过点P分别向坐标轴作垂线段,若两垂线段与坐标轴围成面积为5的矩形,则符合条件的点P个数为
(
▲
)
A.2
B.3
C.4
D.无数个
10、如图,在矩形ABCD中,AB=,AD=9,点P是AD边上的一个动点,连接BP,将矩形ABCD沿BP折叠,得到△A1PB,连接A1C,取A1C的三等分点Q(CQ<A1Q),当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( ▲ )
A.π
B.
C.
D.
二、填空题(本大题共8小题,每小题2分,共16分.不需要写出解答过程,只需把答案直接填写在答卷相应的横线上.)
11、分解因式:a3﹣4a= ▲.
12、去年无锡GDP(国民生产总值)总量实现约916
000
000
000元,该数据用科学记数法表示为
▲
元.
13、已知点M(m,n)与点N(-2,-3)关于x轴对称,则m+n=
▲
.
14、命题“内错角相等”的逆命题是
▲
命题.(填“真”或“假”)
15、圆锥的底面半径为14cm,母线长为21cm,则该圆锥的侧面展开图的圆心角为 ▲ 度.
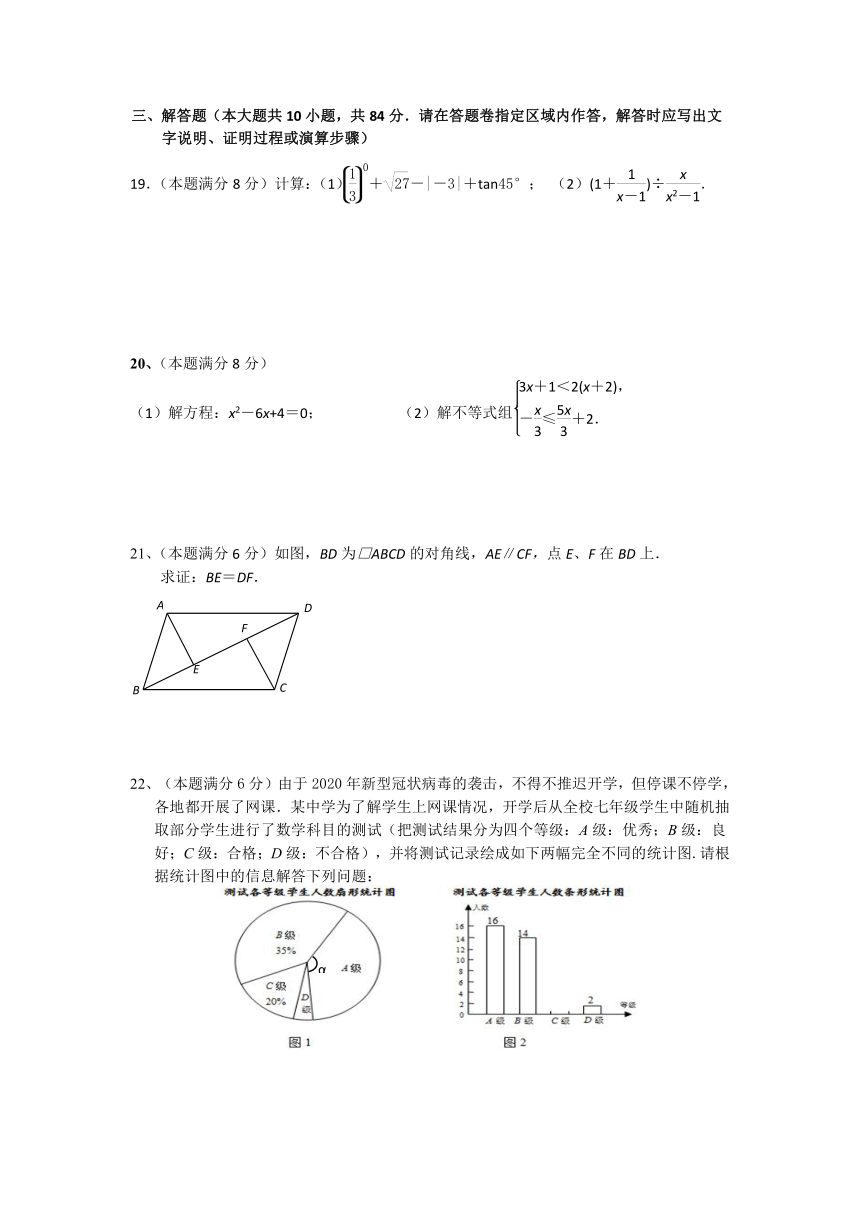
16、一次函数y1=mx+n与y2=﹣x+a的图象如图所示,则0<mx+n<﹣x+a的解集为▲ .
15题
16题
18题
17、在平面直角坐标系中,已知A(3,0),B是以M(3,4)为圆心,1为半径的圆周上的一个动点,连结BO,设BO的中点为C,则线段AC的最小值为
▲
.
18、如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为 ▲ .
三、解答题(本大题共10小题,共84分.请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19.(本题满分8分)计算:(1);
(2)(1+)÷.
20、(本题满分8分)
(1)解方程:x2―6x+4=0;
(2)解不等式组
21、(本题满分6分)如图,BD为□ABCD的对角线,AE∥CF,点E、F在BD上.
求证:BE=DF.
22、(本题满分6分)由于2020年新型冠状病毒的袭击,不得不推迟开学,但停课不停学,各地都开展了网课.某中学为了解学生上网课情况,开学后从全校七年级学生中随机抽取部分学生进行了数学科目的测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:合格;D级:不合格),并将测试记录绘成如下两幅完全不同的统计图.请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生数是多少?
(2)求图1中A级扇形的圆心角∠α的度数,并把图2中的条形统计图补充完成;
(3)该中学七年级共有1200名学生,如果全部参加这次数学科目测试,请估计不合格的人数.
23、(本题满分8分)为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池、过期药品等有害垃圾;B类指剩余食品等厨余垃圾;C类指塑料、废纸等可回收物;D类指其他垃圾.小明投放了一袋垃圾,小亮投放了两袋不同类垃圾.
(1)直接写出小明投放的垃圾恰好是A类的概率是
▲
;
(2)如果小明投放的垃圾是A类,请用画树状图或列表的方法求小亮投放的垃圾恰有一袋与小明投放的垃圾是同类的概率.
24.(本题满分8分)已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=时,求⊙O的半径.
25、(本题满分8分)数学中我们学习了尺规作图,小明发现有些作图只用一种工具就可以完成,你能解决下列问题吗?
(1)请只用无刻度的直尺完成下列作图,不写画法,保留画图痕迹(用虚线表示画图过程,实线表示画图结果)
在图1中,过点A画一条直线把正五边形ABCDE分成面积相等的两部分;
(2)已知直线l及l外一点A(按下列要求作图,不写画法,保留画图痕迹).
①在图2中,只用圆规在直线l上画出两点B、C,使得点A、B、C是一个等腰三角形的三个顶点;
②在图3中,只用圆规在直线l外画出一点P,使得点A、P所在直线与直线l平行.
26、(本题满分10分)水果店购进某种水果的成本为10元/千克,经市场调研,获得销售单价p(元/千克)与销售时间t(1≤t≤15,t为整数)(天)之间的部分数据如下表:
销售时间t(1≤t≤15,t为整数)(天)
1
4
5
8
12
销售单价p(元/千克)
20.25
21
21.25
22
23
已知p与t之间的变化规律符合一次函数关系.
(1)试求p关于t的函数表达式;
(2)若该水果的日销量y(千克)与销售时间t(天)的关系满足一次函数y=-2t+120(1≤t≤15,t为整数).
①
求销售过程中最大日销售利润为多少?
②
在实际销售的前12天中,公司决定每销售1千克水果就捐赠n元利润(n<3)给“精准扶贫”对象.现发现:在前12天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
27、(本题满分10分)在四边形AEBC中,点P是平面内不与点A、C重合的任意一点,连接AP,将线段AP绕点P逆时针旋转与∠ACB相同的度数得到线段DP,连接AD、BD、CP.
(1)观察猜想
如图1,当四边形AEBC为菱形,且∠ACB=60°时,的值是
▲
,直线BD与直线CP相交所成的较小角的度数是
▲
°;
(2)类比探究
如图2,当四边形AEBC为正方形时,请写出的值及直线BD与直线CP相交所成的较小角的度数,并就图2的情形说明理由;
(3)解决问题
当四边形AEBC为正方形时,若点M、N分别是CA、CB的中点,点P在直线MN上,请直接写出点C、P、D在同一直线上时的值.
(本题满分12分)
如图1,在平面直角坐标系中,抛物线y=ax2-2ax+3与x轴交于点A,B(点A在点B的左侧),交y轴于点C,点A的坐标为(-1,0),点D为抛物线的顶点,对称轴与x轴交于点E.
(1)填空:a=
▲
,点B的坐标是
▲
;
(2)连结BD,点M是线段BD上一动点(点M不与端点B,D重合),过点M作MN⊥BD,交抛物线于点N(点N在对称轴的右侧),过点N作NH⊥x轴,垂足为H,交BD于点F,点P是线段OC上一动点,当△MNF的周长取得最大值时,求FP+PC的最小值;
(3)在(2)中,当△MNF的周长取得最大值时,FP+PC取得最小值时,如图2,把点P向下平移个单位得到点Q,连结AQ,把△AOQ绕点O顺时针旋转一定的角度α
(0°<α<360°),得到△A′OQ′,其中边A′Q′交坐标轴于点G.在旋转过程中,是否存在一点G,使得GQ′=OG?若存在,请直接写出所有满足条件的点Q′的坐标;若不存在,请说明理由.
数学试卷
(考试时间:120分钟
试卷分值:130分)
一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是正确的,请把正确的选项填涂在答卷相应的位置.)
1、﹣4的相反数
( ▲ )
A.
B.4
C.﹣4
D.±4
2、下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( ▲ )
3、函数y=中自变量x的取值范围是
(▲)
A.x>2
B.x≥2
C.x≤2
D.x≠2
4、下列运算正确的是
( ▲ )
A.
B.
C.
D.
5、如图是由5个相同的正方体搭成的几何体,其左视图是
( ▲ )
6、为了调查某小区居民的用水情况,随机抽查了若干户家庭的月用水量,结果如下表:
月用水量(吨)
3
4
5
8
户数
2
3
4
1
则关于这若干户家庭的月用水量,下列说法中错误的是( ▲ )
A.调查了10户家庭的月用水量
B.平均数是4.6
C.众数是4
D.中位数是4.5
7、如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,
若∠ACE=25°,则∠D的度数是( ▲ )
A.50°
B.55°
C.60°
D.65°
8、如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0)、B(0,6)分别在x轴、y轴上,反比例函数的图象经过点D,则k值为( ▲ )
A.-14
B.14
C.7
D.-7
7题
8题
10题
9、在平面直角坐标系中,一次函数的图像上有一点P,过点P分别向坐标轴作垂线段,若两垂线段与坐标轴围成面积为5的矩形,则符合条件的点P个数为
(
▲
)
A.2
B.3
C.4
D.无数个
10、如图,在矩形ABCD中,AB=,AD=9,点P是AD边上的一个动点,连接BP,将矩形ABCD沿BP折叠,得到△A1PB,连接A1C,取A1C的三等分点Q(CQ<A1Q),当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( ▲ )
A.π
B.
C.
D.
二、填空题(本大题共8小题,每小题2分,共16分.不需要写出解答过程,只需把答案直接填写在答卷相应的横线上.)
11、分解因式:a3﹣4a= ▲.
12、去年无锡GDP(国民生产总值)总量实现约916
000
000
000元,该数据用科学记数法表示为
▲
元.
13、已知点M(m,n)与点N(-2,-3)关于x轴对称,则m+n=
▲
.
14、命题“内错角相等”的逆命题是
▲
命题.(填“真”或“假”)
15、圆锥的底面半径为14cm,母线长为21cm,则该圆锥的侧面展开图的圆心角为 ▲ 度.
16、一次函数y1=mx+n与y2=﹣x+a的图象如图所示,则0<mx+n<﹣x+a的解集为▲ .
15题
16题
18题
17、在平面直角坐标系中,已知A(3,0),B是以M(3,4)为圆心,1为半径的圆周上的一个动点,连结BO,设BO的中点为C,则线段AC的最小值为
▲
.
18、如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为 ▲ .
三、解答题(本大题共10小题,共84分.请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19.(本题满分8分)计算:(1);
(2)(1+)÷.
20、(本题满分8分)
(1)解方程:x2―6x+4=0;
(2)解不等式组
21、(本题满分6分)如图,BD为□ABCD的对角线,AE∥CF,点E、F在BD上.
求证:BE=DF.
22、(本题满分6分)由于2020年新型冠状病毒的袭击,不得不推迟开学,但停课不停学,各地都开展了网课.某中学为了解学生上网课情况,开学后从全校七年级学生中随机抽取部分学生进行了数学科目的测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:合格;D级:不合格),并将测试记录绘成如下两幅完全不同的统计图.请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生数是多少?
(2)求图1中A级扇形的圆心角∠α的度数,并把图2中的条形统计图补充完成;
(3)该中学七年级共有1200名学生,如果全部参加这次数学科目测试,请估计不合格的人数.
23、(本题满分8分)为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池、过期药品等有害垃圾;B类指剩余食品等厨余垃圾;C类指塑料、废纸等可回收物;D类指其他垃圾.小明投放了一袋垃圾,小亮投放了两袋不同类垃圾.
(1)直接写出小明投放的垃圾恰好是A类的概率是
▲
;
(2)如果小明投放的垃圾是A类,请用画树状图或列表的方法求小亮投放的垃圾恰有一袋与小明投放的垃圾是同类的概率.
24.(本题满分8分)已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=时,求⊙O的半径.
25、(本题满分8分)数学中我们学习了尺规作图,小明发现有些作图只用一种工具就可以完成,你能解决下列问题吗?
(1)请只用无刻度的直尺完成下列作图,不写画法,保留画图痕迹(用虚线表示画图过程,实线表示画图结果)
在图1中,过点A画一条直线把正五边形ABCDE分成面积相等的两部分;
(2)已知直线l及l外一点A(按下列要求作图,不写画法,保留画图痕迹).
①在图2中,只用圆规在直线l上画出两点B、C,使得点A、B、C是一个等腰三角形的三个顶点;
②在图3中,只用圆规在直线l外画出一点P,使得点A、P所在直线与直线l平行.
26、(本题满分10分)水果店购进某种水果的成本为10元/千克,经市场调研,获得销售单价p(元/千克)与销售时间t(1≤t≤15,t为整数)(天)之间的部分数据如下表:
销售时间t(1≤t≤15,t为整数)(天)
1
4
5
8
12
销售单价p(元/千克)
20.25
21
21.25
22
23
已知p与t之间的变化规律符合一次函数关系.
(1)试求p关于t的函数表达式;
(2)若该水果的日销量y(千克)与销售时间t(天)的关系满足一次函数y=-2t+120(1≤t≤15,t为整数).
①
求销售过程中最大日销售利润为多少?
②
在实际销售的前12天中,公司决定每销售1千克水果就捐赠n元利润(n<3)给“精准扶贫”对象.现发现:在前12天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
27、(本题满分10分)在四边形AEBC中,点P是平面内不与点A、C重合的任意一点,连接AP,将线段AP绕点P逆时针旋转与∠ACB相同的度数得到线段DP,连接AD、BD、CP.
(1)观察猜想
如图1,当四边形AEBC为菱形,且∠ACB=60°时,的值是
▲
,直线BD与直线CP相交所成的较小角的度数是
▲
°;
(2)类比探究
如图2,当四边形AEBC为正方形时,请写出的值及直线BD与直线CP相交所成的较小角的度数,并就图2的情形说明理由;
(3)解决问题
当四边形AEBC为正方形时,若点M、N分别是CA、CB的中点,点P在直线MN上,请直接写出点C、P、D在同一直线上时的值.
(本题满分12分)
如图1,在平面直角坐标系中,抛物线y=ax2-2ax+3与x轴交于点A,B(点A在点B的左侧),交y轴于点C,点A的坐标为(-1,0),点D为抛物线的顶点,对称轴与x轴交于点E.
(1)填空:a=
▲
,点B的坐标是
▲
;
(2)连结BD,点M是线段BD上一动点(点M不与端点B,D重合),过点M作MN⊥BD,交抛物线于点N(点N在对称轴的右侧),过点N作NH⊥x轴,垂足为H,交BD于点F,点P是线段OC上一动点,当△MNF的周长取得最大值时,求FP+PC的最小值;
(3)在(2)中,当△MNF的周长取得最大值时,FP+PC取得最小值时,如图2,把点P向下平移个单位得到点Q,连结AQ,把△AOQ绕点O顺时针旋转一定的角度α
(0°<α<360°),得到△A′OQ′,其中边A′Q′交坐标轴于点G.在旋转过程中,是否存在一点G,使得GQ′=OG?若存在,请直接写出所有满足条件的点Q′的坐标;若不存在,请说明理由.
同课章节目录
