第22章 四边形 单元测试-2020-2021学年沪教版(上海)八年级数学第二学期(Word版含答案)
文档属性
| 名称 | 第22章 四边形 单元测试-2020-2021学年沪教版(上海)八年级数学第二学期(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 367.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 00:00:00 | ||
图片预览



文档简介
第二十二章 四边形 单元测试
一、单选题
1.给出下列3个命题,其中真命题的个数是( ).
①单位向量都相等;②单位向量都平行;③平行的单位向量必相等.
A.1个 B.2个 C.3个 D.0个
2.下列命题中,错误的是( )
A.一组对边平行的四边形是梯形;
B.两组对边分别相等的四边形是平行四边形;
C.对角线相等的平行四边形是矩形;
D.一组邻边相等的平行四边形是菱形.
3.一个多边形的每个内角都是135°,则其内角和为( )
A.900° B.1080° C.1260° D.1440°
4.在平行四边形中,设,,点是对角线与的交点,那么向量可以表示为( )
A.; B.; C.; D..
5.如图所示,一个等边三角形纸片剪去一个角后变成一个四边形,则图中的度数为( )
A. B. C. D.
6.如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则此梯形的中位线的长是( )
A.10 B. C. D.12
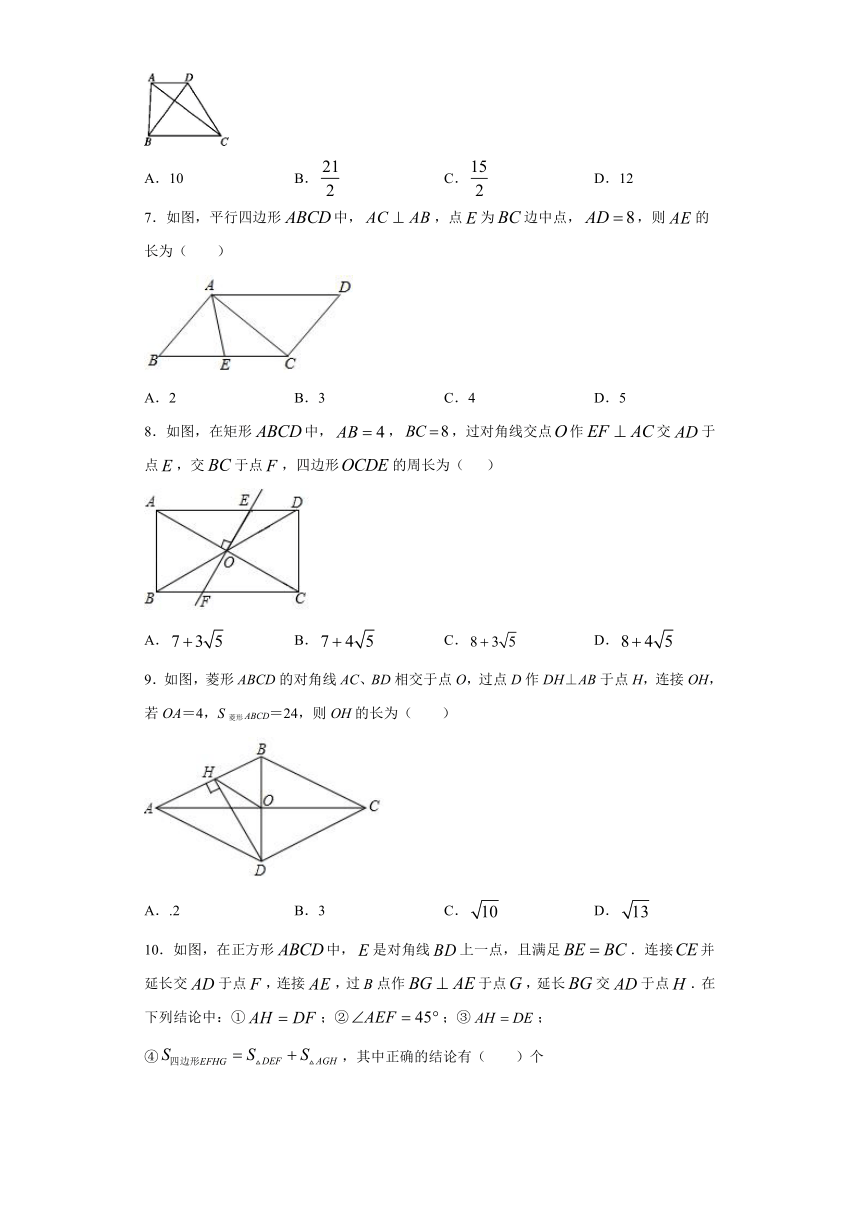
7.如图,平行四边形中,,点为边中点,,则的长为( )
A.2 B.3 C.4 D.5
8.如图,在矩形中,,,过对角线交点作交于点,交于点,四边形的周长为( )
A. B. C. D.
9.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=4,S菱形ABCD=24,则OH的长为( )
A..2 B.3 C. D.
10.如图,在正方形中,是对角线上一点,且满足.连接并延长交于点,连接,过点作于点,延长交于点.在下列结论中:①;②;③;④,其中正确的结论有( )个
A.1 B.2 C.3 D.4
二、填空题
11.已知一个多边形的每一个内角都等于,则这个多边形的边数是_______.
12.在菱形中,已知,,那么__________(结果用向量,的式子表示).
13.已知一个正多边形的内角和为1260°,则这个正多边形的每个外角比每个内角小__度.
14.等腰梯形的周长为,中位线长为,则腰长为____.
15.梯形中,,,,那么____.
16.如图,在平行四边形中,,平分交边于点,且,则的长为__.
17.如图,矩形OABC的顶点B的坐标为(2,3),则AC=_____.
18.如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,若△OED的面积是5,则四边形OECB的面积是______
19.如图,在菱形ABCD中,AB=8,∠B=60°,点E在边AD上,且AE=3.若过点E的直线l,将该菱形的面积平分,且与菱形的另一边交于点F,则线段EF的长为_____.
20.如图,ABCD为正方形,O为AC、BD的交点,△DCE为直角三角形,∠CED=90°,∠DCE=30°,若正方形的边长为2,则OE的长为__________.
三、解答题
21.一个多边形的内角和是它外角和的3倍,它是几边形?
22.根据图中所给的向量,分别画出下列向量.
(1);
(2).
23.如图,在平行四边形ABCD中,E、F是对角线AC上的两点,AE=CF.求证:四边形BEDF是平行四边形.
24.如图,四边形ABCD中,ABDC,AC平分∠BAD,CEDA交AB于点E.求证:四边形ADCE是菱形.
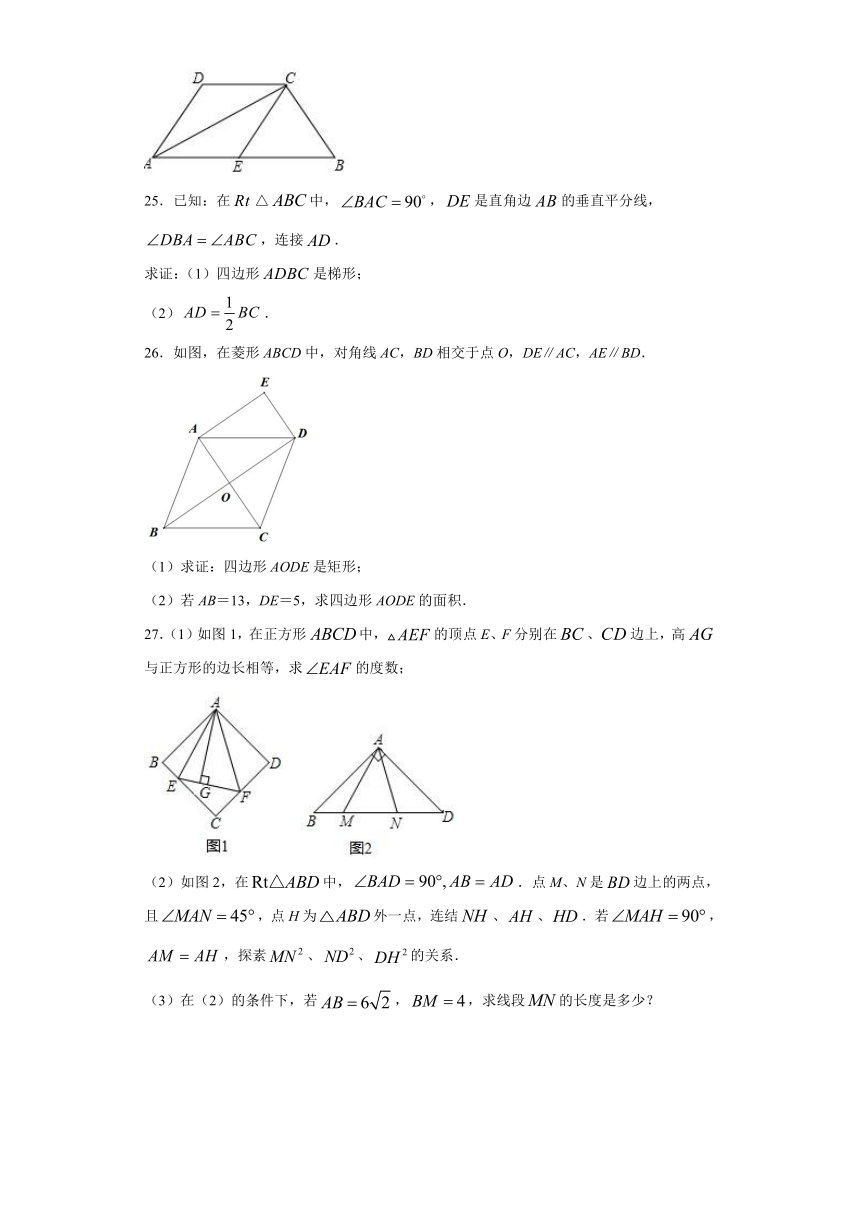
25.已知:在△中,,是直角边的垂直平分线,,连接.
求证:(1)四边形是梯形;
(2).
26.如图,在菱形ABCD中,对角线AC,BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=13,DE=5,求四边形AODE的面积.
27.(1)如图1,在正方形中,的顶点E、F分别在、边上,高与正方形的边长相等,求的度数;
(2)如图2,在中,.点M、N是边上的两点,且,点H为外一点,连结、、.若,,探素、、的关系.
(3)在(2)的条件下,若,,求线段的长度是多少?
参考答案
1.D
2.A
3.B
4.A
5.C
6.C
7.C
8.A
9.B
10.C
11.9
12.
13.100
14.7.
15..
16.2
17.
18.15.
19.
20..
21.这个多边形是八边形
22.解:根据三角形法则进行解题,图形见下图,
23.证明:∵平行四边形ABCD中,
∴AB//CD且AB=CD,
∴,
∵AE=CF,
∴△ABE≌△CDF(SAS)
∴BE=DF
同理可证△AED≌△CFB
∴BF=ED
∴四边形BEDF是平行四边形.
24.∵,,
∴四边形是平行四边形,
∵平分,
∴,
又∵,
∴,
∴,
∴.
又∵四边形是平行四边形,
∴四边形是菱形.
25.证明:(1)如图,
∵DE是AB的垂直平分线,
∴AD=BD,
∴∠DBA=∠DAB,
∵∠DBA=∠ABC,
∴∠ABC=DAB,
∴AD∥BC,
∵AC与BD不平行,
∴四边形ADBC是梯形,
(2)如图,延长DE交BC于F,
∵∠DBA=∠ABC,BE=BE,∠DEB=∠BEF=90°,
∴△BDE≌△BFE,
∴BF=BD=AD,
∵∠BAC=∠BEF=90°,
∴DF∥AC,
∵AD∥BC,
∴四边形ACFD是平行四边形,
∴AD=FC,FC=BF=AD,
∴.
26.(1)证明:,,
四边形AODE是平行四边形,
在菱形ABCD中,,
,
四边形AODE是矩形;
(2)解:四边形AODE是矩形,
,
四边形ABCD是菱形,
,,
,
,
四边形AODE的面积.
27.解:(1)∵四边形是正方形,
∴,
∵,
∴,
∴(HL),
∴,
同理可得,
∵,
∴,
∴;
(2),理由如下:
∵,
∴,
∵,,
∴,
∵,
∴(SAS),
∴,
∴,
∵,
∴,
∵AN=AN,
∴(SAS),
∴,
∴在Rt△HDN中,,
∴;
(3)由(2)得,,,
∵,
∴,
∵,
∴设,则有,
∴,
解得:,
∴.
一、单选题
1.给出下列3个命题,其中真命题的个数是( ).
①单位向量都相等;②单位向量都平行;③平行的单位向量必相等.
A.1个 B.2个 C.3个 D.0个
2.下列命题中,错误的是( )
A.一组对边平行的四边形是梯形;
B.两组对边分别相等的四边形是平行四边形;
C.对角线相等的平行四边形是矩形;
D.一组邻边相等的平行四边形是菱形.
3.一个多边形的每个内角都是135°,则其内角和为( )
A.900° B.1080° C.1260° D.1440°
4.在平行四边形中,设,,点是对角线与的交点,那么向量可以表示为( )
A.; B.; C.; D..
5.如图所示,一个等边三角形纸片剪去一个角后变成一个四边形,则图中的度数为( )
A. B. C. D.
6.如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则此梯形的中位线的长是( )
A.10 B. C. D.12
7.如图,平行四边形中,,点为边中点,,则的长为( )
A.2 B.3 C.4 D.5
8.如图,在矩形中,,,过对角线交点作交于点,交于点,四边形的周长为( )
A. B. C. D.
9.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=4,S菱形ABCD=24,则OH的长为( )
A..2 B.3 C. D.
10.如图,在正方形中,是对角线上一点,且满足.连接并延长交于点,连接,过点作于点,延长交于点.在下列结论中:①;②;③;④,其中正确的结论有( )个
A.1 B.2 C.3 D.4
二、填空题
11.已知一个多边形的每一个内角都等于,则这个多边形的边数是_______.
12.在菱形中,已知,,那么__________(结果用向量,的式子表示).
13.已知一个正多边形的内角和为1260°,则这个正多边形的每个外角比每个内角小__度.
14.等腰梯形的周长为,中位线长为,则腰长为____.
15.梯形中,,,,那么____.
16.如图,在平行四边形中,,平分交边于点,且,则的长为__.
17.如图,矩形OABC的顶点B的坐标为(2,3),则AC=_____.
18.如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,若△OED的面积是5,则四边形OECB的面积是______
19.如图,在菱形ABCD中,AB=8,∠B=60°,点E在边AD上,且AE=3.若过点E的直线l,将该菱形的面积平分,且与菱形的另一边交于点F,则线段EF的长为_____.
20.如图,ABCD为正方形,O为AC、BD的交点,△DCE为直角三角形,∠CED=90°,∠DCE=30°,若正方形的边长为2,则OE的长为__________.
三、解答题
21.一个多边形的内角和是它外角和的3倍,它是几边形?
22.根据图中所给的向量,分别画出下列向量.
(1);
(2).
23.如图,在平行四边形ABCD中,E、F是对角线AC上的两点,AE=CF.求证:四边形BEDF是平行四边形.
24.如图,四边形ABCD中,ABDC,AC平分∠BAD,CEDA交AB于点E.求证:四边形ADCE是菱形.
25.已知:在△中,,是直角边的垂直平分线,,连接.
求证:(1)四边形是梯形;
(2).
26.如图,在菱形ABCD中,对角线AC,BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=13,DE=5,求四边形AODE的面积.
27.(1)如图1,在正方形中,的顶点E、F分别在、边上,高与正方形的边长相等,求的度数;
(2)如图2,在中,.点M、N是边上的两点,且,点H为外一点,连结、、.若,,探素、、的关系.
(3)在(2)的条件下,若,,求线段的长度是多少?
参考答案
1.D
2.A
3.B
4.A
5.C
6.C
7.C
8.A
9.B
10.C
11.9
12.
13.100
14.7.
15..
16.2
17.
18.15.
19.
20..
21.这个多边形是八边形
22.解:根据三角形法则进行解题,图形见下图,
23.证明:∵平行四边形ABCD中,
∴AB//CD且AB=CD,
∴,
∵AE=CF,
∴△ABE≌△CDF(SAS)
∴BE=DF
同理可证△AED≌△CFB
∴BF=ED
∴四边形BEDF是平行四边形.
24.∵,,
∴四边形是平行四边形,
∵平分,
∴,
又∵,
∴,
∴,
∴.
又∵四边形是平行四边形,
∴四边形是菱形.
25.证明:(1)如图,
∵DE是AB的垂直平分线,
∴AD=BD,
∴∠DBA=∠DAB,
∵∠DBA=∠ABC,
∴∠ABC=DAB,
∴AD∥BC,
∵AC与BD不平行,
∴四边形ADBC是梯形,
(2)如图,延长DE交BC于F,
∵∠DBA=∠ABC,BE=BE,∠DEB=∠BEF=90°,
∴△BDE≌△BFE,
∴BF=BD=AD,
∵∠BAC=∠BEF=90°,
∴DF∥AC,
∵AD∥BC,
∴四边形ACFD是平行四边形,
∴AD=FC,FC=BF=AD,
∴.
26.(1)证明:,,
四边形AODE是平行四边形,
在菱形ABCD中,,
,
四边形AODE是矩形;
(2)解:四边形AODE是矩形,
,
四边形ABCD是菱形,
,,
,
,
四边形AODE的面积.
27.解:(1)∵四边形是正方形,
∴,
∵,
∴,
∴(HL),
∴,
同理可得,
∵,
∴,
∴;
(2),理由如下:
∵,
∴,
∵,,
∴,
∵,
∴(SAS),
∴,
∴,
∵,
∴,
∵AN=AN,
∴(SAS),
∴,
∴在Rt△HDN中,,
∴;
(3)由(2)得,,,
∵,
∴,
∵,
∴设,则有,
∴,
解得:,
∴.
