八年级数学上册 《5.1函数》(第2课时)课件 苏科版
文档属性
| 名称 | 八年级数学上册 《5.1函数》(第2课时)课件 苏科版 |  | |
| 格式 | zip | ||
| 文件大小 | 308.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-05 22:02:35 | ||
图片预览





文档简介
(共17张PPT)
5.1函数(2)
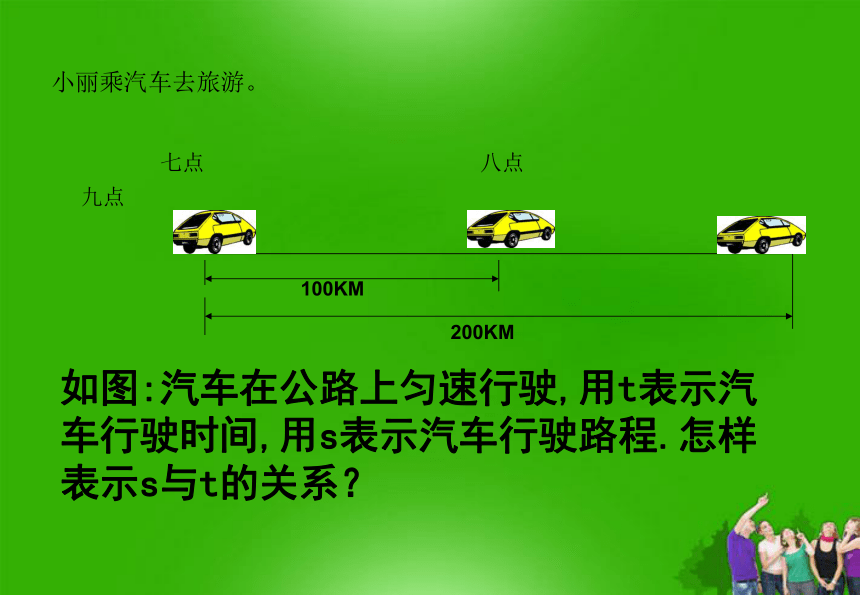
小丽乘汽车去旅游。
七点 八点 九点
100KM
200KM
如图:汽车在公路上匀速行驶,用t表示汽车行驶时间,用s表示汽车行驶路程.怎样表示s与t的关系?
(1)可以列表表示:
t h 1 2 3 4 5 6 ……
s km 100 200 300 400 ……
500
600
(2)可以用解析式表示
s=100t
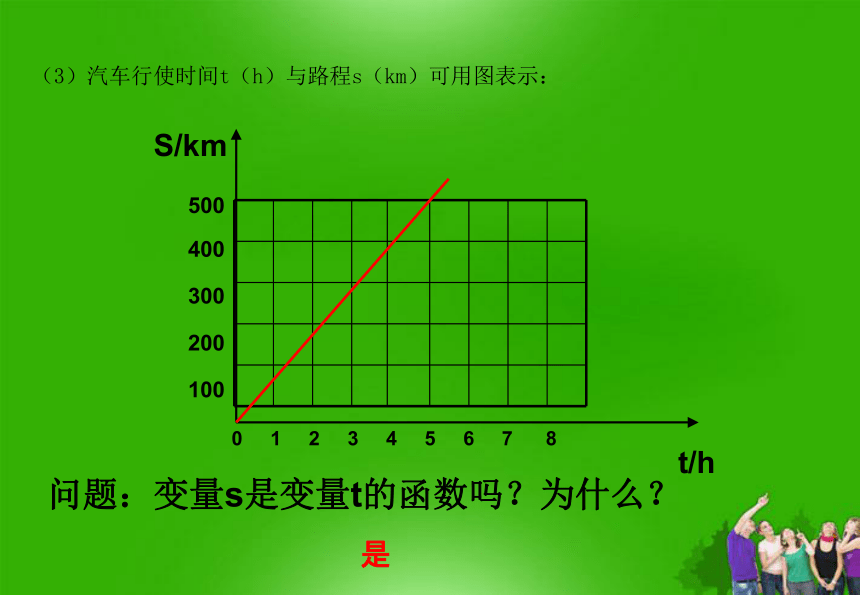
(3)汽车行使时间t(h)与路程s(km)可用图表示:
0 1 2 3 4 5 6 7 8
500
400
300
200
100
t/h
S/km
问题:变量s是变量t的函数吗?为什么?
是
通常,表示2个变量之间的关系可用3种方法: 、 、 。
列表
图形
数学式子
表示两个变量之间关系的式子通常称为函数关系式
例如:s=100t 就称为s与t的函数关系式
在一个变化过程中,自变量的取值通常有一定的范围,如无特别说明,一般要求写出函数关系式时必须写上自变量的取值范围,否则默认为自变量取一切实数。
求下列函数的自变量取值范围:
y=13x-4;
求函数自变量取值范围:
①函数的解析式是整式时,自变量可取一切实数;
②函数的解析式是分式时,自变量的取值应使分母≠0;
③函数的解析式是二次根式时,自变量的取值应使被开方数≥0。
④函数的解析式是三次根式时,自变量的取值应是一切实数。
⑤自变量在零次幂、负整数指数幂底数中时,自变量的取值应使底数不为0.
⑥同时出现几种代数式,取各种代数式中自变量取值范围的公共部分.
⑥对于反映实际问题的函数关系,应使实际问题有意义。
例1:汽车油箱内存油40 L,每行驶100KM耗油10L,求行驶过程中油箱内剩余油量Q L与行驶路程s km的函数关系式
在太阳和月球引力的影响下,海水定时涨落的现象称为潮汐:
图中的平滑曲线,如实记录了当天每一时刻的潮位,揭示了这一天里潮位y(M)与时间T(H)之间的函数关系
0 2 4 6 8 10 12 14 16 18 20 22 24
2.5
2.0
1.5
1.0
0.5
y(m)
t (h)
像这样,在直角坐标系中,如果描出以自变量的值为横坐标,相应的函数值为纵坐标的点,那么所有这样的点组成的图形叫做这个函数的图象.
例2:小明骑自行车从甲地到乙地,图中的折线表示小明的行程S(千米)和所花时间t(小时)之间的函数关系:(1)他在路上花了多长时间
(2)折线中有一条平行于X轴的线段,试说明它的意义.
(3)出发后5小时,他离甲地有多远
P(5,30)
t
S
50
40
30
20
10
…………………….....
0 1 2 3 4 5 7
…………...
………...
…………
……….
…………………
在例题中,给定一个自变量的值,就可以求出对应的函数值。
例如,例2中的自变量的值取4时,对应的函数值是20。
求下列函数当x=3时的函数值:
(1)y=6x-4; (2)y=-5x2;
(3)y=
巩固练习:
1、某种报纸的单价为b元,x表示购买的这种报纸的份数,那么购买报纸的总价y与x的关系为 .
2.打字收费标准是每千字5元,打字费m(元)与字数a的函数关系式为 ,自变量a的取值范围是 .
3.在函数关系式y=- x+2中,
当x=-3时,y= ;当y=0时,x=____.
4.拖拉机的油箱装油40kg,犁地平均每小时耗油3kg,拖拉机工作x h后,油箱剩下油y kg.则y与x间的函数关系式是_________.
5.函数y 中自变量x的取值范围是 ;当x 时,y=_________.
6.某种储蓄的年利率为2.5%,存入1000元本金后,则本息和y(元)与所存年数x之间的关系式为 ;4年后的本息和为 元(此利息要交纳所得税的20%).
5.1函数(2)
小丽乘汽车去旅游。
七点 八点 九点
100KM
200KM
如图:汽车在公路上匀速行驶,用t表示汽车行驶时间,用s表示汽车行驶路程.怎样表示s与t的关系?
(1)可以列表表示:
t h 1 2 3 4 5 6 ……
s km 100 200 300 400 ……
500
600
(2)可以用解析式表示
s=100t
(3)汽车行使时间t(h)与路程s(km)可用图表示:
0 1 2 3 4 5 6 7 8
500
400
300
200
100
t/h
S/km
问题:变量s是变量t的函数吗?为什么?
是
通常,表示2个变量之间的关系可用3种方法: 、 、 。
列表
图形
数学式子
表示两个变量之间关系的式子通常称为函数关系式
例如:s=100t 就称为s与t的函数关系式
在一个变化过程中,自变量的取值通常有一定的范围,如无特别说明,一般要求写出函数关系式时必须写上自变量的取值范围,否则默认为自变量取一切实数。
求下列函数的自变量取值范围:
y=13x-4;
求函数自变量取值范围:
①函数的解析式是整式时,自变量可取一切实数;
②函数的解析式是分式时,自变量的取值应使分母≠0;
③函数的解析式是二次根式时,自变量的取值应使被开方数≥0。
④函数的解析式是三次根式时,自变量的取值应是一切实数。
⑤自变量在零次幂、负整数指数幂底数中时,自变量的取值应使底数不为0.
⑥同时出现几种代数式,取各种代数式中自变量取值范围的公共部分.
⑥对于反映实际问题的函数关系,应使实际问题有意义。
例1:汽车油箱内存油40 L,每行驶100KM耗油10L,求行驶过程中油箱内剩余油量Q L与行驶路程s km的函数关系式
在太阳和月球引力的影响下,海水定时涨落的现象称为潮汐:
图中的平滑曲线,如实记录了当天每一时刻的潮位,揭示了这一天里潮位y(M)与时间T(H)之间的函数关系
0 2 4 6 8 10 12 14 16 18 20 22 24
2.5
2.0
1.5
1.0
0.5
y(m)
t (h)
像这样,在直角坐标系中,如果描出以自变量的值为横坐标,相应的函数值为纵坐标的点,那么所有这样的点组成的图形叫做这个函数的图象.
例2:小明骑自行车从甲地到乙地,图中的折线表示小明的行程S(千米)和所花时间t(小时)之间的函数关系:(1)他在路上花了多长时间
(2)折线中有一条平行于X轴的线段,试说明它的意义.
(3)出发后5小时,他离甲地有多远
P(5,30)
t
S
50
40
30
20
10
…………………….....
0 1 2 3 4 5 7
…………...
………...
…………
……….
…………………
在例题中,给定一个自变量的值,就可以求出对应的函数值。
例如,例2中的自变量的值取4时,对应的函数值是20。
求下列函数当x=3时的函数值:
(1)y=6x-4; (2)y=-5x2;
(3)y=
巩固练习:
1、某种报纸的单价为b元,x表示购买的这种报纸的份数,那么购买报纸的总价y与x的关系为 .
2.打字收费标准是每千字5元,打字费m(元)与字数a的函数关系式为 ,自变量a的取值范围是 .
3.在函数关系式y=- x+2中,
当x=-3时,y= ;当y=0时,x=____.
4.拖拉机的油箱装油40kg,犁地平均每小时耗油3kg,拖拉机工作x h后,油箱剩下油y kg.则y与x间的函数关系式是_________.
5.函数y 中自变量x的取值范围是 ;当x 时,y=_________.
6.某种储蓄的年利率为2.5%,存入1000元本金后,则本息和y(元)与所存年数x之间的关系式为 ;4年后的本息和为 元(此利息要交纳所得税的20%).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
