小学数学西师大版五年级下 3.5问题解决 课件(17张ppt)
文档属性
| 名称 | 小学数学西师大版五年级下 3.5问题解决 课件(17张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-28 17:40:18 | ||
图片预览





文档简介
问 题 解 决
第 2 课 时
五年级下册第三单元
引入新知
▲. 回顾长方体和正方体的体积公式
▲. 创设情境(学生用准备好的橡皮泥 捏出不同的形体)
长方体的体积 =长×宽×高
正方体的体积 =棱长×棱长×棱长
长(正)方体的体积=底面积×高
出示情境
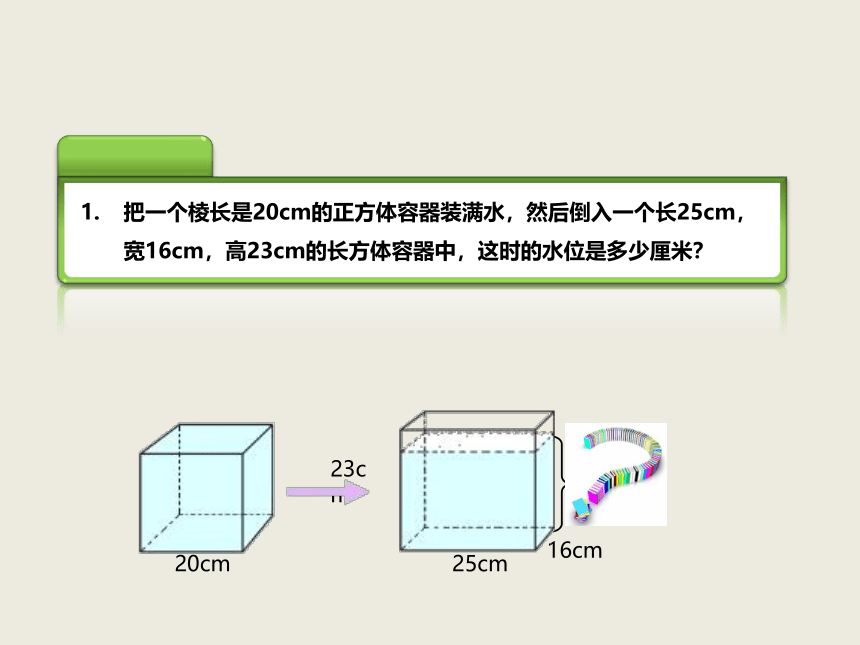
把一个棱长是20cm的正方体容器装满水,然后倒入一个长25cm,宽16cm,高23cm的长方体容器中,这时的水位是多少厘米?
25cm
16cm
23cm
20cm
把一个棱长是20cm的正方体容器装满水,然后倒入一个长25cm,宽16cm,高23cm的长方体容器中,这时的水位是多少厘米?
课堂探索与分析
已知正方体容器的棱长和长方体容器的……
正方体容器中水的体积与长方体容器中水体积相等。
课堂探索与分析
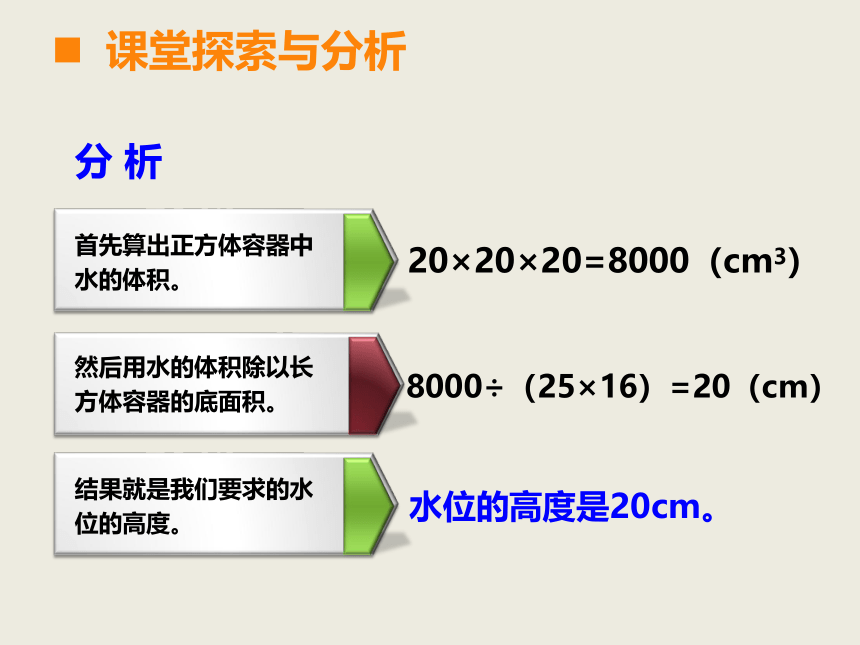
分 析
结果就是我们要求的水位的高度。
首先算出正方体容器中水的体积。
然后用水的体积除以长方体容器的底面积。
20×20×20=8000(cm3)
8000÷(25×16)=20(cm)
水位的高度是20cm。
课堂探索与分析
20×20×20=8000(cm3)
25×16×23=9200 ( cm3)
9200-8000=1200 ( cm3)
1200 ÷(25×16) =3 ( cm )
23-3 = 20 ( cm )
答:这时的水位是20 cm。
。
25cm
16cm
23cm
20cm
课堂活动
小实验:
测量红薯的体积。
放入前
放入后
课堂探索与分析
将一个红薯放入盛有一定量水的长方体容器里。
观察放入红薯前后,
水的高度的变化,并记录在下表里。
课堂探索与分析
放入前
放入后
长(cm)
宽(cm)
高(cm)
水的体积(cm3)
1.8
0.8
0.9
1.8
0.8
1.2
1.296
1.728
问题解决
红薯的体积=放入后水的体积-放入前水的体积
首先算出放入红薯前水的体积。
然后算出放入红薯后水的体积。
长×宽×放入前水的高
长×宽×放入后水的高
红薯的体积=升高的水的体积
想一想,议一议
请同学们充分想象,思考一下,还有其他的测量方法吗?
放入红薯前后,水的长、宽、高哪些是变化的,哪些是不变的呢?
?
?
课堂练习
在一个长16cm、宽10cm、高20cm长方体玻璃缸中,装入一个棱长为8cm正方体铁块,然后往缸中注一些水,使它完全淹没这个正方体铁块,当铁块从缸中取出时,
请同学们思考一下,水为什么会下降?铁块的体积转化成了哪部分水的体积?
缸中的水会下降多少厘米?
课堂探索与分析
分 析
要用“等积变换”知识来解此题。
减少的水的体积=铁块的体积
16cm
16cm
10cm
20cm
20cm
10cm
8cm
问题解决
结果就是我们要求的水下降多少厘米。
首先算出铁块的体积。
然后用这个体积除以长方体容器的底面积。
8×8×8=512(cm3)
512÷(16×10)=3.2(cm)
水位下降3.2cm。
通过本节课的学习,你学到了什么?
课堂总结
师生同获
学会运用“等积变换”的思想来解决实际问题。要掌握已知物体的体积,求与体积相关数量的变式问题。
第 2 课 时
五年级下册第三单元
引入新知
▲. 回顾长方体和正方体的体积公式
▲. 创设情境(学生用准备好的橡皮泥 捏出不同的形体)
长方体的体积 =长×宽×高
正方体的体积 =棱长×棱长×棱长
长(正)方体的体积=底面积×高
出示情境
把一个棱长是20cm的正方体容器装满水,然后倒入一个长25cm,宽16cm,高23cm的长方体容器中,这时的水位是多少厘米?
25cm
16cm
23cm
20cm
把一个棱长是20cm的正方体容器装满水,然后倒入一个长25cm,宽16cm,高23cm的长方体容器中,这时的水位是多少厘米?
课堂探索与分析
已知正方体容器的棱长和长方体容器的……
正方体容器中水的体积与长方体容器中水体积相等。
课堂探索与分析
分 析
结果就是我们要求的水位的高度。
首先算出正方体容器中水的体积。
然后用水的体积除以长方体容器的底面积。
20×20×20=8000(cm3)
8000÷(25×16)=20(cm)
水位的高度是20cm。
课堂探索与分析
20×20×20=8000(cm3)
25×16×23=9200 ( cm3)
9200-8000=1200 ( cm3)
1200 ÷(25×16) =3 ( cm )
23-3 = 20 ( cm )
答:这时的水位是20 cm。
。
25cm
16cm
23cm
20cm
课堂活动
小实验:
测量红薯的体积。
放入前
放入后
课堂探索与分析
将一个红薯放入盛有一定量水的长方体容器里。
观察放入红薯前后,
水的高度的变化,并记录在下表里。
课堂探索与分析
放入前
放入后
长(cm)
宽(cm)
高(cm)
水的体积(cm3)
1.8
0.8
0.9
1.8
0.8
1.2
1.296
1.728
问题解决
红薯的体积=放入后水的体积-放入前水的体积
首先算出放入红薯前水的体积。
然后算出放入红薯后水的体积。
长×宽×放入前水的高
长×宽×放入后水的高
红薯的体积=升高的水的体积
想一想,议一议
请同学们充分想象,思考一下,还有其他的测量方法吗?
放入红薯前后,水的长、宽、高哪些是变化的,哪些是不变的呢?
?
?
课堂练习
在一个长16cm、宽10cm、高20cm长方体玻璃缸中,装入一个棱长为8cm正方体铁块,然后往缸中注一些水,使它完全淹没这个正方体铁块,当铁块从缸中取出时,
请同学们思考一下,水为什么会下降?铁块的体积转化成了哪部分水的体积?
缸中的水会下降多少厘米?
课堂探索与分析
分 析
要用“等积变换”知识来解此题。
减少的水的体积=铁块的体积
16cm
16cm
10cm
20cm
20cm
10cm
8cm
问题解决
结果就是我们要求的水下降多少厘米。
首先算出铁块的体积。
然后用这个体积除以长方体容器的底面积。
8×8×8=512(cm3)
512÷(16×10)=3.2(cm)
水位下降3.2cm。
通过本节课的学习,你学到了什么?
课堂总结
师生同获
学会运用“等积变换”的思想来解决实际问题。要掌握已知物体的体积,求与体积相关数量的变式问题。
