天津市天津一中2020-2021学年高一下学期期中考试数学试题 PDF版含答案
文档属性
| 名称 | 天津市天津一中2020-2021学年高一下学期期中考试数学试题 PDF版含答案 |  | |
| 格式 | |||
| 文件大小 | 495.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 09:08:18 | ||
图片预览




文档简介
天津 一中 2020- 2021- 2 高一 年级 数学 学科 期中 质量 调查 试卷
本试 卷分 为第 I 卷( 选择 题) 、第 II 卷( 非选 择题 )两 部分 ,共 100 分, 考试 用时 90 分
钟。 考生 务必 将答 案涂 写在 答题 纸的 规定 位置 上, 答在 试卷 上的 无效 。
祝各 位考 生考 试顺 利!
参考 公式 :
柱体 的体 积公 式V Sh? .其中S 表示 柱体 的底 面积 ,h表示 柱体 的高 .
1
锥体 的体 积公 式V ? Sh.其中 S 表示 锥体 的底 面面 积,h表示 锥体 的高 .
3
圆锥 的侧 面积 公式S= .其中r是底 面圆 的半 径,l是母 线长 .
球的 表面 积公 式S= ,体积 公式V= .其中r是球 的半 径.
第 Ⅰ卷
一. 选择 题: (每 小题 3 分, 共 30 分) 在每 小题 给出 的四 个选 项中 ,只 有一 项是 符合 题目 要求
的.
? ? ? ?
1.如 果a,b是两 个单 位向 量, 则a与b一定 ( )
A .相 等 B.平 行 C.方 向相 同 D .长 度相 等
2.下 列命 题正 确的 是( )
A. 三点 确定 一个 平面 B. 一条 直线 和一 个点 确定 一个 平面
C. 梯形 可确 定一 个平 面 D. 圆心 和圆 上两 点确 定一 个平 面
2
3.若 复数z x x i? ? ? ?? ?1 1? ? 为纯 虚数 ,则 实数x的值 为( )
A .-1 B. 0 C. 1 D .-1 或 1
4.若P为两 条异 面直 线l m, 外的 任意 一点 ,则 ( )
A.过 点P有且 仅有 一条 直线 与l m, 都平 行
B.过 点P有且 仅有 一条 直线 与l m, 都垂 直
C.过 点P有且 仅有 一条 直线 与l m, 都相 交
D.过 点P有且 仅有 一条 直线 与l m, 都异 面
5.设?ABC的内 角A,B,C所对 的边 分别 为a,b,c,若b C c B a Acos cos sin? ? ,则
?ABC的形 状为 ( )
A .锐 角三 角形 B.直 角三 角形 C.钝 角三 角形 D .不 确定
? ? ? ? ?
6. 已知 向量 ?
a b x? ?(1, 1), ( 2, ),若a b? 与4 2b a? 平行 ,则 实数x的值 是( )
A. -2 B. 0 C. 1 D. 2
???? ????
7. △ABC的三 边长 分别 为AB=7,BC=5,CA=6,则A B B C? 的值 为( )
A. -19 B. -14 C. 14 D. 19
2?z
8. 设复 数z ? ? ?1 i(i为虚 数单 位) ,z的共 轭复 数为z ,则 等于 ( )
z
A. ? ?1 2i B. ? ?2 i C. ? ?1 2i D. 1 2? i
9. 已知 三棱 柱 的侧 棱垂 直于 底面 ,各 顶点 都在 同一 球面 上, 若该 棱柱 的体 积为
, , , ,则 此球 的表 面积 等于 ( )
A. B. C. D.
10.如 图是 一个 正方 体的 平面 展开 图, 在这 个正 方体 中
①BM ED// ②EF CD/ /
③C N 与BM 为异 面直 线 ④DM BN?
以上 四个 命题 中, 正确 的序 号是 ( )
A. ①② ③ B.②④ C .③④ D .②③ ④
第Ⅱ 卷
二. 填空 题: (本 大题 共 6 小题 ,每 小题 4 分, 共 24 分)
1?7i
11. 若i为虚 数单 位, 复数z ? ,则| |z ?_____ ___.
1?i
12. 在正 方体ABC A B C DD? 1 1 1 1中, 对角 线A C1与底 面ABCD所成 角的 正弦 值为 _____ _____ __.
13. 如图 ,在 四边 形 ABCD 中, AB⊥ BC, AB=6, BC=8, △AC D 是等 边三 角???? ????
形, 则AC BD? 的值 为_____ _____ ____ _.
14. 一艘 轮船 按照 北偏 东40?方向 ,以 18 海里 / 时的 速度 直线 航行 ,一 座灯 塔原 来在 轮船 的南 偏
东20?方向 上, 经过 20 分钟 的航 行, 轮船 与灯 塔的 距离 为6 3海里 ,则 灯塔 与轮 船原 来的 距离
为
15.若 将一 个圆 锥的 侧面 沿一 条母 线展 开, 其展 开图 是半 径为 5,面 积为1 5?的扇 形, 则与 该圆
锥等 体积 的球 的半 径为 _____ __.
16. 在△ABC中,AB AC BAC? ?4 3 = 90, , ∠ ,? D在边BC上, 延长AD到P,使 得AP=9,若
???? ???? 3 ????
PA?mPB?( ?m)PC(m为常 数) ,则CD的长 度是 _____ ___ .
2
三. 解答 题: 本大 题共 4 小题 共 46 分。 解答 应写 出文 字说 明, 证明 过程 或演 算步 骤.
1
17. 已知?A B C 的内 角A B C, , 的对 边分 别是a b c, , ,且a B b At a n t a n? ,cosC ? ,
4
c?3.
(1 )求cosA的值 ;
(2 )求?A B C 的面 积 .
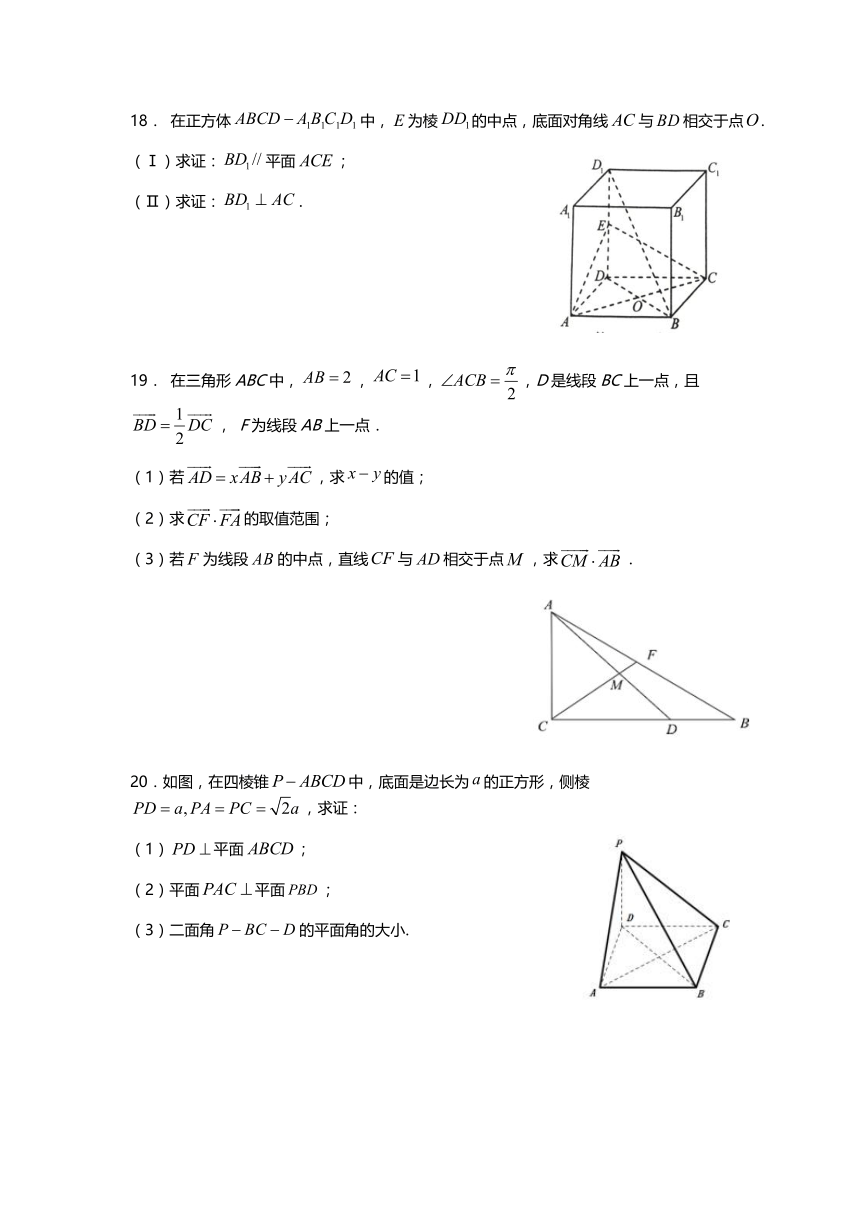
18. 在正 方体ABC D A B C D? 1 1 1 1中,E为棱D D1的中 点, 底面 对角 线AC与B D相交 于点O.
(Ⅰ )求 证:BD1/ /平面ACE;
(Ⅱ )求 证:BD AC1 ? .
?
19. 在三 角形ABC中,A B ?2,AC ?1,?ACB? ,D是线 段BC上一 点, 且
2
???? 1????
BD ? DC , F为线 段AB上一 点.
2
???? ???? ????
(1 )若AD x AB y AC? ? ,求x y? 的值 ;
???? ????
(2 )求CF FA? 的取 值范 围;
????? ????
(3 )若F 为线 段A B的中 点, 直线CF 与A D相交 于点M ,求CM AB? .
20.如 图, 在四 棱锥P ABCD? 中, 底面 是边 长为a的正 方形 ,侧 棱
PD ?a,PA? PC ? 2a,求 证:
(1 )PD?平面ABCD;
(2 )平 面PAC ?平面PBD;
(3 )二 面角P B C D? ? 的平 面角 的大 小 .
参考 答案 :
1.【答 案】 D
2.【答 案】 C
【解 析】
对于 A 选项 ,三 个不 在同 一条 直线 上的 点, 确定 一个 平面 ,故 A 选项 错误 .
对于 B 选项 ,直 线和 直线 外一 点, 确定 一个 平面 ,故 B 选项 错误 .
对于 C 选项 ,两 条平 行直 线确 定一 个平 面, 梯形 有一 组对 边平 行, 另一 组对 边不 平行 ,故 梯形 可
确定 一个 平面 ,所 以 C 选项 正确 .
对于 D 选项 ,圆 的直 径不 能确 定一 个平 面, 所以 若圆 心和 圆上 的两 点在 直径 上, 则无 法确 定一
个平 面.所以 D 选项 错误 .
故选 :C
3.【答 案】 A
4.【答 案】 B
【解 析】
解: 因为 若点P是两 条异 面直 线l m, 外的 任意 一点 ,则 过点P有且 仅有 一条 直线 与l m, 都垂
直, 选 B
5.【答 案】 B
6.【答 案】 D
【解 析】 ? ? ? ? ? ? ? ?
【 详 解 】 因 为 a b x? ?(1, 1), ( 2, ) , 所 以 a b x b a x? ? ? ? ? ?(3, 1), 4 2 ( 6, 4 2), 由 于 a b? 与
? ?
4 2b a? 平行 ,得6( 1) 3( 4 2) 0x x? ? ? ? ,解 得x?2.
7.【答 案】 A
【解 析】
【详 解】 解: 由于AB?7,BC ?5,CA?6,
25?49?36 19
则cosB? ? ,
2?5?7 35
???? ???? ???? ????
则AB BC AB BC B? ? ??| | | | cos( )??
19
?7?5?(? )??19.
35
故选 :A .
8.【答 案】 C
【解 析】
2?z 3?i ?2?4i
【详 解】 因为 ? ? ??1?2i,
z ?1?i 2
故选 C.
9.【答 案】 A
10.【答 案】 D
【解 析】
作出 正方 体得 到直 观图 如图 所示 :
由直 观图 可知 ,BM 与DE为互 相垂 直的 异面 直线 , 故① 不正 确;
EF AB CD/ / / / ,故② 正确 ;
C N 与BM 为异 面直 线,故 ③正确 ;
由正 方体 性质 可知BN ?平面DEM ,故BN DM? , 故④ 正确 .
故选 :D
11.【答 案】 5
【解 析】
1?7i (1?7i)(1?i) ?6?8i
解:z? ? ? ??3? 4i 2 2
,则|z|? (?3) ?(?4) ?5.
1?i (1?i)(1?i) 2
故答 案为 :5 .
3
12.【答 案】 3
【解 析】
连结AC,
则AC是A1C在平 面ABCD上的射影 ,
则∠A1CA即为 直线A1C与平 面ABCD所成 角的正弦 值,
设正 方体 的棱 长为 1,
则 ,
则 ,
13.【答 案】 14.
【解 析】
3
【 详 解 】 AB ⊥ BC , AB=6 , BC=8 , ∴ AC=10 , ∴ cos ∠ BAC= ; 又 △ ACD 是
5
1 ???? ???? ???? ????
等 边 三 角 形 , ∴ AD =AC=10 , cos ∠ CA D= , ∴ AC ?B D= AC ? ( A D﹣
2
???? ???? ???? ???? ????
A B)=AC?A D﹣AC?A B
1 3
=10×10 × ﹣10 ×6× =14.
2 5
14.【答 案】 6 海里
【分 析】
根据 方位 角可 知 ?
? ?C A B 1 2 0 ,利 用余 弦定 理构 造方 程可 解得 结果 .
【 详 解 】 记 轮 船 最 初 位 置 为 A, 灯 塔 位 置 为B,20分 钟 后 轮 船 位 置 为C,
如下 图所 示:
1
由题 意得 : ? ? ? ?
AC ?18? ?6,? ? ? ? ?C A B 1 8 0 4 0 2 0 1 2 0 ,
3
BC ?6 3
2 2 2 2
AC ?AB ?BC 36? AB ?108 1
则cos?CAB? ,即 : ?? ,解 得:
2AC?AB 12AB 2
AB?6
即灯 塔与 轮船 原来 的距 离为6海里
15.【答 案】3 9
【解 析】
1
由扇 形面 积和 半径 ,设 扇形 的半 径为r,弧 长为l,则 可得S ? lr,
2
1
由题 意:15?? ?5?l, ?l ?6?,
2
设圆 锥的 底面 半径 为r?,则2 6 , 3? ?r r? ?? ? ? ,该 圆锥 的高 2 2
h? 5 ?3 ?4,
1 2 1 2
圆锥 体积V ? ?r? ?h? ?3 ?4?12?,
3 3
4 3
设球 的半 径为R,由 题意 得 ?R ?12?,
3
3
?R? 9,
故答 案为 :3 9.
16.
18
【答 案】 0 或 5 ???? ????
【解 析】 ∵A D P, , 三点 共线 ,∴ 可设PA PD? ?? ?? ?0 ,
???? ???? ?3 ????? ???? ???? ?3 ?
?3 ????? ? ?m?
∵PA?mPB?? ?m?PC ,∴?PD?mPB?? ?m?PC,即???? m???? ?2 ?????,
?2 ? ?2 ? PD? PB? PC
? ?
3
若m?0且m? ,则B D C, , 三点 共线 ,
2
?3 ?
? ?m? 3
∴m ?2
? ? ,即?? ,
?1
? ? 2
∵AP?9, ∴AD?3,
∵A B ?4,AC ?3,? ? ?BAC 90 ,∴BC ?5,
设CD x? ,? ?CDA ?,则BD x? ?5 ,? ? ?BDA ? ?.
2 2 2 2 2 2 2
AD ?CD ?AC x AD BD AB? ? ? ?5 7? ?x
∴根据 余弦 定理 可得cos?? ? ,cos? ?? ?? ? ? ,
2AD?CD 6 2AD BD? 6 5? ??x
∵cos cos 0? ? ?? ? ?? ? ,
2
x ?5?x? ?7 18
∴ ? ?0,解 得x? ,
6 6?5?x? 5
18
∴C D的长 度为 .
5
???? 3????
当m?0时, PA? PC,C D, 重合 ,此 时C D的长 度为0,
2
3 ???? 3????
当m? 时,PA? PB,B D, 重合 ,此 时P A?1 2,不 合题 意, 舍去 .
2 2
18
故答 案为 :0 或 .
5
17.
asinB bsinA
【解 析】( 1)因 为a B b At a n t a n? ,则 ? ,
cosB cosA
由正 弦定 理可 得cosA cosB? ,又A B, 0,?? ?? ,故 可得A B? ;
2
又因 为cosC A B cos A A? ? ? ? ? ? ?cos? ? 2 1 2 cos ,
2 3 6
代值 可得cos A? ,解 得cosA?? .
8 4
? ?? 6
又A B? ,由 内角 和定 理可 知A??0,? ?,故cosA? .
? 2 ? 4
1 15 6 10
(2 )因 为cosC ? ,故 可得sinC ? ;cosA? ,故 可得sinA? .
4 4 4 4
csinA
由正 弦定 理可 得a ? ? 6 ?b,
sinC
1 1 15 3 15
故可 得三 角形ABC面积S ? absinC ? ?6? ? .
2 2 4 4
18.
【解 析】
(Ⅰ )连 结OE,在 正方 体ABC D A B C D? 1 1 1 1中,
因为OB OD? ,E为棱D D1的中 点, 所以B D O E1/ / ,
又因 为OE?平面ACE,BD1? 平面ACE,
所以BD1/ /平面ACE;
(Ⅱ )在 正方 体ABC D A B C D? 1 1 1 1中,
由AC BD? ,D D1 ?面ABCD,AC ?面ABCD,所 以
DD AC1 ? ,
又因 为B D?面BDD1,DD1 ?面BDD1,BD DD D? 1 ? ,所 以A C ?面BDD1,
又由BD1 ?面BDD1,所 以BD AC1 ? .
1 ? 1 ? 4
19. 【答 案】(1 ) ;(2)??3, ?;( 3) .
3 ? 16? 5
【解 析】
???? 1???? ???? ???? 1 ???? ???? 3???? ???? 1????
(1 )因 为BD ? DC ,所 以AD? AB ? ?AC? AD?,即 AD ? AB? AC,
2 2 2 2
uuur 2uuur 1uuur ???? ???? ???? 2 1
所以AD ? AB? AC ,又AD x AB y AC? ? ,所 以x? ,y ? ,
3 3 3 3
1
因此x? y ? ;
3
?
(2 )因 为在 三角 形ABC中,A B ?2,AC ?1,?ACB ? ,
2
? ???? ???? ???? ???? ???? ???? ???? ???? ????
所以?CAB ? ,BC ? 3,因 此C F FA C A AF FA C A FA AF FA? ? ? ? ? ? ? ?? ? ,
3
????
设 AF ? x,由 题意 ,x?? ?0, 2 ,
所以
2
???? ???? ???? ???? ???? ???? ???? ???? ???? 2 1 2 ? 1? 1
CF?FA?CA?FA?AF?FA? CA ? FA cos?CAB? AF ? x?x ???x? ? ? ,
2 ? 4? 16
2
? 1? 1 ? 1 ?
因为x?? ?0, 2 ,所 以??x? ? ? ???3, ?;
? 4? 16 ? 16?
???? ???? 1???? 1???? 1????
(3 )因 为F 为线 段A B 的中 点, 所以CF ?CA? AB ? CA? CB,
2 2 2
????? ???? ????? ????
因为 直线CF 与A D相交 于点M ,不 妨设C M C F? ? ?? ?? ?0 1 ,AM AD? ? ?? ?? ?0 1 ,
????? ????? ?????
所以CM ? CA? CB,
2 2
????? ????? ???? ?? ????? ?????
因此AM ?CM ?CA?? ?1?CA? CB,
? 2 ? 2
???? ???? ???? 2???? ???? ????? ?2???? ?????
又 AD ?CD?CA? CB?CA,所 以AM ??? CB?CA?,
3 ?3 ?
?? ????? ????? ?2???? ?????
因此? ?1?CA? CB ??? CB?CA?,
? 2 ? 2 ?3 ?
??
? ?1???
?2 4
所以? ,解 得:?? ,
?? 2 5
? ?
??2 3
????? ???? ?2???? 2????? ???? ???? 2????2 2????2 4
所以CM ?AB ?? CA? CB???CB?CA?? CB ? CA ? .
?5 5 ? 5 5 5
20.【答 案 】( 1)见 解析 ;(2 )见 解析 ;( 3) ?
45
2 2 2
【解 析】( 1)?PD ?a,DC ?a,PC ? 2a,? ? ?P C P D D C .
? ?P D D C .
同理 可证P D A D? .Q AD DC D? ? ,
? ?P D 平面ABCD.
(2 )由 (1)知PD?平面ABCD,?AC ?平面
ABCD,? ?P D A C.
∵四边 形ABCD是正 方形 ,? ?AC BD.
又Q BD PD D? ? ,? ?AC 平面PBD.
又?AC ?平面PAC,∴平面PAC ?平面PBD.
(3 )由 (1)知PD?平面ABCD,BC?平面
ABCD,? ?P D B C .
又Q B C DC P D DC D? ? ?, ,? ?BC 平面P D C .
?PC?平面P D C ,? ?BC PC.
? ?PCD为二 面角P B C D? ? 的平 面角 .
在Rt?PDC中,PD DC a PC D? ? ? ? ? ?, 45 .
∴二面 角P B C D? ? 的平 面角 的大 小为 45 °.
本试 卷分 为第 I 卷( 选择 题) 、第 II 卷( 非选 择题 )两 部分 ,共 100 分, 考试 用时 90 分
钟。 考生 务必 将答 案涂 写在 答题 纸的 规定 位置 上, 答在 试卷 上的 无效 。
祝各 位考 生考 试顺 利!
参考 公式 :
柱体 的体 积公 式V Sh? .其中S 表示 柱体 的底 面积 ,h表示 柱体 的高 .
1
锥体 的体 积公 式V ? Sh.其中 S 表示 锥体 的底 面面 积,h表示 锥体 的高 .
3
圆锥 的侧 面积 公式S= .其中r是底 面圆 的半 径,l是母 线长 .
球的 表面 积公 式S= ,体积 公式V= .其中r是球 的半 径.
第 Ⅰ卷
一. 选择 题: (每 小题 3 分, 共 30 分) 在每 小题 给出 的四 个选 项中 ,只 有一 项是 符合 题目 要求
的.
? ? ? ?
1.如 果a,b是两 个单 位向 量, 则a与b一定 ( )
A .相 等 B.平 行 C.方 向相 同 D .长 度相 等
2.下 列命 题正 确的 是( )
A. 三点 确定 一个 平面 B. 一条 直线 和一 个点 确定 一个 平面
C. 梯形 可确 定一 个平 面 D. 圆心 和圆 上两 点确 定一 个平 面
2
3.若 复数z x x i? ? ? ?? ?1 1? ? 为纯 虚数 ,则 实数x的值 为( )
A .-1 B. 0 C. 1 D .-1 或 1
4.若P为两 条异 面直 线l m, 外的 任意 一点 ,则 ( )
A.过 点P有且 仅有 一条 直线 与l m, 都平 行
B.过 点P有且 仅有 一条 直线 与l m, 都垂 直
C.过 点P有且 仅有 一条 直线 与l m, 都相 交
D.过 点P有且 仅有 一条 直线 与l m, 都异 面
5.设?ABC的内 角A,B,C所对 的边 分别 为a,b,c,若b C c B a Acos cos sin? ? ,则
?ABC的形 状为 ( )
A .锐 角三 角形 B.直 角三 角形 C.钝 角三 角形 D .不 确定
? ? ? ? ?
6. 已知 向量 ?
a b x? ?(1, 1), ( 2, ),若a b? 与4 2b a? 平行 ,则 实数x的值 是( )
A. -2 B. 0 C. 1 D. 2
???? ????
7. △ABC的三 边长 分别 为AB=7,BC=5,CA=6,则A B B C? 的值 为( )
A. -19 B. -14 C. 14 D. 19
2?z
8. 设复 数z ? ? ?1 i(i为虚 数单 位) ,z的共 轭复 数为z ,则 等于 ( )
z
A. ? ?1 2i B. ? ?2 i C. ? ?1 2i D. 1 2? i
9. 已知 三棱 柱 的侧 棱垂 直于 底面 ,各 顶点 都在 同一 球面 上, 若该 棱柱 的体 积为
, , , ,则 此球 的表 面积 等于 ( )
A. B. C. D.
10.如 图是 一个 正方 体的 平面 展开 图, 在这 个正 方体 中
①BM ED// ②EF CD/ /
③C N 与BM 为异 面直 线 ④DM BN?
以上 四个 命题 中, 正确 的序 号是 ( )
A. ①② ③ B.②④ C .③④ D .②③ ④
第Ⅱ 卷
二. 填空 题: (本 大题 共 6 小题 ,每 小题 4 分, 共 24 分)
1?7i
11. 若i为虚 数单 位, 复数z ? ,则| |z ?_____ ___.
1?i
12. 在正 方体ABC A B C DD? 1 1 1 1中, 对角 线A C1与底 面ABCD所成 角的 正弦 值为 _____ _____ __.
13. 如图 ,在 四边 形 ABCD 中, AB⊥ BC, AB=6, BC=8, △AC D 是等 边三 角???? ????
形, 则AC BD? 的值 为_____ _____ ____ _.
14. 一艘 轮船 按照 北偏 东40?方向 ,以 18 海里 / 时的 速度 直线 航行 ,一 座灯 塔原 来在 轮船 的南 偏
东20?方向 上, 经过 20 分钟 的航 行, 轮船 与灯 塔的 距离 为6 3海里 ,则 灯塔 与轮 船原 来的 距离
为
15.若 将一 个圆 锥的 侧面 沿一 条母 线展 开, 其展 开图 是半 径为 5,面 积为1 5?的扇 形, 则与 该圆
锥等 体积 的球 的半 径为 _____ __.
16. 在△ABC中,AB AC BAC? ?4 3 = 90, , ∠ ,? D在边BC上, 延长AD到P,使 得AP=9,若
???? ???? 3 ????
PA?mPB?( ?m)PC(m为常 数) ,则CD的长 度是 _____ ___ .
2
三. 解答 题: 本大 题共 4 小题 共 46 分。 解答 应写 出文 字说 明, 证明 过程 或演 算步 骤.
1
17. 已知?A B C 的内 角A B C, , 的对 边分 别是a b c, , ,且a B b At a n t a n? ,cosC ? ,
4
c?3.
(1 )求cosA的值 ;
(2 )求?A B C 的面 积 .
18. 在正 方体ABC D A B C D? 1 1 1 1中,E为棱D D1的中 点, 底面 对角 线AC与B D相交 于点O.
(Ⅰ )求 证:BD1/ /平面ACE;
(Ⅱ )求 证:BD AC1 ? .
?
19. 在三 角形ABC中,A B ?2,AC ?1,?ACB? ,D是线 段BC上一 点, 且
2
???? 1????
BD ? DC , F为线 段AB上一 点.
2
???? ???? ????
(1 )若AD x AB y AC? ? ,求x y? 的值 ;
???? ????
(2 )求CF FA? 的取 值范 围;
????? ????
(3 )若F 为线 段A B的中 点, 直线CF 与A D相交 于点M ,求CM AB? .
20.如 图, 在四 棱锥P ABCD? 中, 底面 是边 长为a的正 方形 ,侧 棱
PD ?a,PA? PC ? 2a,求 证:
(1 )PD?平面ABCD;
(2 )平 面PAC ?平面PBD;
(3 )二 面角P B C D? ? 的平 面角 的大 小 .
参考 答案 :
1.【答 案】 D
2.【答 案】 C
【解 析】
对于 A 选项 ,三 个不 在同 一条 直线 上的 点, 确定 一个 平面 ,故 A 选项 错误 .
对于 B 选项 ,直 线和 直线 外一 点, 确定 一个 平面 ,故 B 选项 错误 .
对于 C 选项 ,两 条平 行直 线确 定一 个平 面, 梯形 有一 组对 边平 行, 另一 组对 边不 平行 ,故 梯形 可
确定 一个 平面 ,所 以 C 选项 正确 .
对于 D 选项 ,圆 的直 径不 能确 定一 个平 面, 所以 若圆 心和 圆上 的两 点在 直径 上, 则无 法确 定一
个平 面.所以 D 选项 错误 .
故选 :C
3.【答 案】 A
4.【答 案】 B
【解 析】
解: 因为 若点P是两 条异 面直 线l m, 外的 任意 一点 ,则 过点P有且 仅有 一条 直线 与l m, 都垂
直, 选 B
5.【答 案】 B
6.【答 案】 D
【解 析】 ? ? ? ? ? ? ? ?
【 详 解 】 因 为 a b x? ?(1, 1), ( 2, ) , 所 以 a b x b a x? ? ? ? ? ?(3, 1), 4 2 ( 6, 4 2), 由 于 a b? 与
? ?
4 2b a? 平行 ,得6( 1) 3( 4 2) 0x x? ? ? ? ,解 得x?2.
7.【答 案】 A
【解 析】
【详 解】 解: 由于AB?7,BC ?5,CA?6,
25?49?36 19
则cosB? ? ,
2?5?7 35
???? ???? ???? ????
则AB BC AB BC B? ? ??| | | | cos( )??
19
?7?5?(? )??19.
35
故选 :A .
8.【答 案】 C
【解 析】
2?z 3?i ?2?4i
【详 解】 因为 ? ? ??1?2i,
z ?1?i 2
故选 C.
9.【答 案】 A
10.【答 案】 D
【解 析】
作出 正方 体得 到直 观图 如图 所示 :
由直 观图 可知 ,BM 与DE为互 相垂 直的 异面 直线 , 故① 不正 确;
EF AB CD/ / / / ,故② 正确 ;
C N 与BM 为异 面直 线,故 ③正确 ;
由正 方体 性质 可知BN ?平面DEM ,故BN DM? , 故④ 正确 .
故选 :D
11.【答 案】 5
【解 析】
1?7i (1?7i)(1?i) ?6?8i
解:z? ? ? ??3? 4i 2 2
,则|z|? (?3) ?(?4) ?5.
1?i (1?i)(1?i) 2
故答 案为 :5 .
3
12.【答 案】 3
【解 析】
连结AC,
则AC是A1C在平 面ABCD上的射影 ,
则∠A1CA即为 直线A1C与平 面ABCD所成 角的正弦 值,
设正 方体 的棱 长为 1,
则 ,
则 ,
13.【答 案】 14.
【解 析】
3
【 详 解 】 AB ⊥ BC , AB=6 , BC=8 , ∴ AC=10 , ∴ cos ∠ BAC= ; 又 △ ACD 是
5
1 ???? ???? ???? ????
等 边 三 角 形 , ∴ AD =AC=10 , cos ∠ CA D= , ∴ AC ?B D= AC ? ( A D﹣
2
???? ???? ???? ???? ????
A B)=AC?A D﹣AC?A B
1 3
=10×10 × ﹣10 ×6× =14.
2 5
14.【答 案】 6 海里
【分 析】
根据 方位 角可 知 ?
? ?C A B 1 2 0 ,利 用余 弦定 理构 造方 程可 解得 结果 .
【 详 解 】 记 轮 船 最 初 位 置 为 A, 灯 塔 位 置 为B,20分 钟 后 轮 船 位 置 为C,
如下 图所 示:
1
由题 意得 : ? ? ? ?
AC ?18? ?6,? ? ? ? ?C A B 1 8 0 4 0 2 0 1 2 0 ,
3
BC ?6 3
2 2 2 2
AC ?AB ?BC 36? AB ?108 1
则cos?CAB? ,即 : ?? ,解 得:
2AC?AB 12AB 2
AB?6
即灯 塔与 轮船 原来 的距 离为6海里
15.【答 案】3 9
【解 析】
1
由扇 形面 积和 半径 ,设 扇形 的半 径为r,弧 长为l,则 可得S ? lr,
2
1
由题 意:15?? ?5?l, ?l ?6?,
2
设圆 锥的 底面 半径 为r?,则2 6 , 3? ?r r? ?? ? ? ,该 圆锥 的高 2 2
h? 5 ?3 ?4,
1 2 1 2
圆锥 体积V ? ?r? ?h? ?3 ?4?12?,
3 3
4 3
设球 的半 径为R,由 题意 得 ?R ?12?,
3
3
?R? 9,
故答 案为 :3 9.
16.
18
【答 案】 0 或 5 ???? ????
【解 析】 ∵A D P, , 三点 共线 ,∴ 可设PA PD? ?? ?? ?0 ,
???? ???? ?3 ????? ???? ???? ?3 ?
?3 ????? ? ?m?
∵PA?mPB?? ?m?PC ,∴?PD?mPB?? ?m?PC,即???? m???? ?2 ?????,
?2 ? ?2 ? PD? PB? PC
? ?
3
若m?0且m? ,则B D C, , 三点 共线 ,
2
?3 ?
? ?m? 3
∴m ?2
? ? ,即?? ,
?1
? ? 2
∵AP?9, ∴AD?3,
∵A B ?4,AC ?3,? ? ?BAC 90 ,∴BC ?5,
设CD x? ,? ?CDA ?,则BD x? ?5 ,? ? ?BDA ? ?.
2 2 2 2 2 2 2
AD ?CD ?AC x AD BD AB? ? ? ?5 7? ?x
∴根据 余弦 定理 可得cos?? ? ,cos? ?? ?? ? ? ,
2AD?CD 6 2AD BD? 6 5? ??x
∵cos cos 0? ? ?? ? ?? ? ,
2
x ?5?x? ?7 18
∴ ? ?0,解 得x? ,
6 6?5?x? 5
18
∴C D的长 度为 .
5
???? 3????
当m?0时, PA? PC,C D, 重合 ,此 时C D的长 度为0,
2
3 ???? 3????
当m? 时,PA? PB,B D, 重合 ,此 时P A?1 2,不 合题 意, 舍去 .
2 2
18
故答 案为 :0 或 .
5
17.
asinB bsinA
【解 析】( 1)因 为a B b At a n t a n? ,则 ? ,
cosB cosA
由正 弦定 理可 得cosA cosB? ,又A B, 0,?? ?? ,故 可得A B? ;
2
又因 为cosC A B cos A A? ? ? ? ? ? ?cos? ? 2 1 2 cos ,
2 3 6
代值 可得cos A? ,解 得cosA?? .
8 4
? ?? 6
又A B? ,由 内角 和定 理可 知A??0,? ?,故cosA? .
? 2 ? 4
1 15 6 10
(2 )因 为cosC ? ,故 可得sinC ? ;cosA? ,故 可得sinA? .
4 4 4 4
csinA
由正 弦定 理可 得a ? ? 6 ?b,
sinC
1 1 15 3 15
故可 得三 角形ABC面积S ? absinC ? ?6? ? .
2 2 4 4
18.
【解 析】
(Ⅰ )连 结OE,在 正方 体ABC D A B C D? 1 1 1 1中,
因为OB OD? ,E为棱D D1的中 点, 所以B D O E1/ / ,
又因 为OE?平面ACE,BD1? 平面ACE,
所以BD1/ /平面ACE;
(Ⅱ )在 正方 体ABC D A B C D? 1 1 1 1中,
由AC BD? ,D D1 ?面ABCD,AC ?面ABCD,所 以
DD AC1 ? ,
又因 为B D?面BDD1,DD1 ?面BDD1,BD DD D? 1 ? ,所 以A C ?面BDD1,
又由BD1 ?面BDD1,所 以BD AC1 ? .
1 ? 1 ? 4
19. 【答 案】(1 ) ;(2)??3, ?;( 3) .
3 ? 16? 5
【解 析】
???? 1???? ???? ???? 1 ???? ???? 3???? ???? 1????
(1 )因 为BD ? DC ,所 以AD? AB ? ?AC? AD?,即 AD ? AB? AC,
2 2 2 2
uuur 2uuur 1uuur ???? ???? ???? 2 1
所以AD ? AB? AC ,又AD x AB y AC? ? ,所 以x? ,y ? ,
3 3 3 3
1
因此x? y ? ;
3
?
(2 )因 为在 三角 形ABC中,A B ?2,AC ?1,?ACB ? ,
2
? ???? ???? ???? ???? ???? ???? ???? ???? ????
所以?CAB ? ,BC ? 3,因 此C F FA C A AF FA C A FA AF FA? ? ? ? ? ? ? ?? ? ,
3
????
设 AF ? x,由 题意 ,x?? ?0, 2 ,
所以
2
???? ???? ???? ???? ???? ???? ???? ???? ???? 2 1 2 ? 1? 1
CF?FA?CA?FA?AF?FA? CA ? FA cos?CAB? AF ? x?x ???x? ? ? ,
2 ? 4? 16
2
? 1? 1 ? 1 ?
因为x?? ?0, 2 ,所 以??x? ? ? ???3, ?;
? 4? 16 ? 16?
???? ???? 1???? 1???? 1????
(3 )因 为F 为线 段A B 的中 点, 所以CF ?CA? AB ? CA? CB,
2 2 2
????? ???? ????? ????
因为 直线CF 与A D相交 于点M ,不 妨设C M C F? ? ?? ?? ?0 1 ,AM AD? ? ?? ?? ?0 1 ,
????? ????? ?????
所以CM ? CA? CB,
2 2
????? ????? ???? ?? ????? ?????
因此AM ?CM ?CA?? ?1?CA? CB,
? 2 ? 2
???? ???? ???? 2???? ???? ????? ?2???? ?????
又 AD ?CD?CA? CB?CA,所 以AM ??? CB?CA?,
3 ?3 ?
?? ????? ????? ?2???? ?????
因此? ?1?CA? CB ??? CB?CA?,
? 2 ? 2 ?3 ?
??
? ?1???
?2 4
所以? ,解 得:?? ,
?? 2 5
? ?
??2 3
????? ???? ?2???? 2????? ???? ???? 2????2 2????2 4
所以CM ?AB ?? CA? CB???CB?CA?? CB ? CA ? .
?5 5 ? 5 5 5
20.【答 案 】( 1)见 解析 ;(2 )见 解析 ;( 3) ?
45
2 2 2
【解 析】( 1)?PD ?a,DC ?a,PC ? 2a,? ? ?P C P D D C .
? ?P D D C .
同理 可证P D A D? .Q AD DC D? ? ,
? ?P D 平面ABCD.
(2 )由 (1)知PD?平面ABCD,?AC ?平面
ABCD,? ?P D A C.
∵四边 形ABCD是正 方形 ,? ?AC BD.
又Q BD PD D? ? ,? ?AC 平面PBD.
又?AC ?平面PAC,∴平面PAC ?平面PBD.
(3 )由 (1)知PD?平面ABCD,BC?平面
ABCD,? ?P D B C .
又Q B C DC P D DC D? ? ?, ,? ?BC 平面P D C .
?PC?平面P D C ,? ?BC PC.
? ?PCD为二 面角P B C D? ? 的平 面角 .
在Rt?PDC中,PD DC a PC D? ? ? ? ? ?, 45 .
∴二面 角P B C D? ? 的平 面角 的大 小为 45 °.
同课章节目录
