第七章 7.1三角形的边(无答案)
文档属性
| 名称 | 第七章 7.1三角形的边(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 29.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-06 07:14:18 | ||
图片预览

文档简介
鸡西市第十九中学学案
学科 数学 课题 三角形的边 课型 新课
时间 2012年 月 日 人教版 七年级下
学习目标 1.认识三角形,了解三角形的意义,认识三角形的边、内角、顶点,能用符号语言表示三角形.2.理解三角形三边不等的关系.
重点难点 三角形三边间的不等关系.用三角形三边不等关系判定三条线段可否组成三角形.
学习内容 学法及设计意图
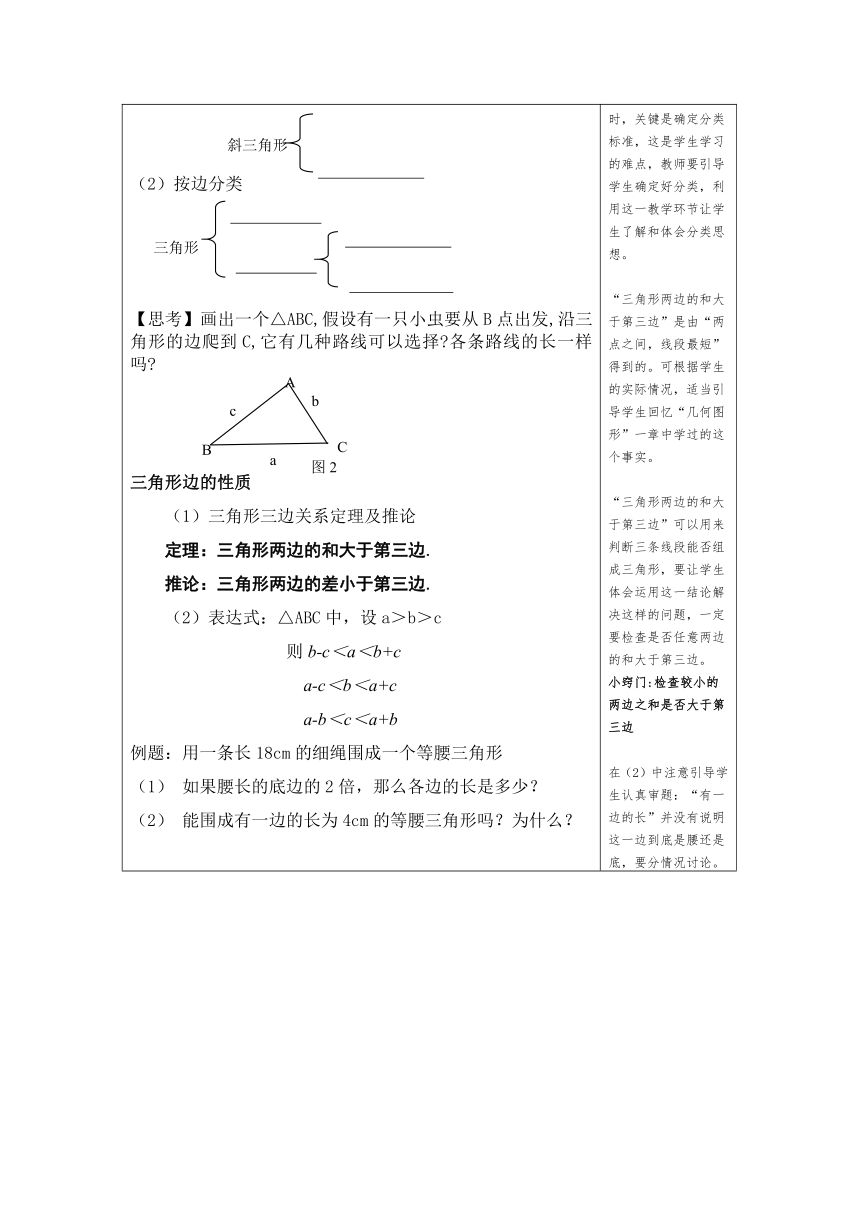
【引入】三角形是一种最常见的几何图形之一.你能举几个例子吗?以下几个图形. 哪些是三角形 【归纳】不在一直线上三条线段首尾顺次相接组成的图形叫做三角形.图1中的三角形记作: 读作: 1、三角形的有关概念及表示(图1)(1)顶点:三角形两边的公共点称为三角形的顶点;的顶点是 , , 。(2)边:组成三角形的三条线段称为三角形的边;的三条边为 , , 。(3)内角:在三角形中,每两条边所组成的角叫做三角形的内角;的三个内角为 , , 。2:三角形的分类三角形分类有两种方法:(1)按角分类;(2)按边分类按角分类 (2)按边分类 【思考】画出一个△ABC,假设有一只小虫要从B点出发,沿三角形的边爬到C,它有几种路线可以选择 各条路线的长一样吗 三角形边的性质
(1)三角形三边关系定理及推论
定理:三角形两边的和大于第三边.推论:三角形两边的差小于第三边.
(2)表达式:△ABC中,设a>b>c
则b-c<a<b+c
a-c<b<a+c
a-b<c<a+b例题:用一条长18cm的细绳围成一个等腰三角形如果腰长的底边的2倍,那么各边的长是多少?能围成有一边的长为4cm的等腰三角形吗?为什么? 引导学生从自然景观到微型模型,从建筑物到艺术作品,甚至日常生活用品中去寻找三角形的实际例子,体现数学来源于生活。三角形的概念,学生在小学也学习过,但需进一步严格定义,教师在这里要强调“首位顺次相接”,利用上面的几个图形说明定义中增加这几个字的必要性。通过学生自学教材88页的前五段内容,独立完成空格的内容。在这里教师要强调(1) 为同一个三角形。(2)角的两边为射线,三角形的三条边为线段。自学教材88页第6段到89页探究以上文字,完成填空。按边把三角形分类时,关键是确定分类标准,这是学生学习的难点,教师要引导学生确定好分类,利用这一教学环节让学生了解和体会分类思想。“三角形两边的和大于第三边”是由“两点之间,线段最短”得到的。可根据学生的实际情况,适当引导学生回忆“几何图形”一章中学过的这个事实。“三角形两边的和大于第三边”可以用来判断三条线段能否组成三角形,要让学生体会运用这一结论解决这样的问题,一定要检查是否任意两边的和大于第三边。小窍门:检查较小的两边之和是否大于第三边在(2)中注意引导学生认真审题:“有一边的长”并没有说明这一边到底是腰还是底,要分情况讨论。
【当堂检测】1.下图中有几个三角形?用符号表示这些三角形.2.下列说法: (1)等边三角形是等腰三角形; (2)三角形按边分类可分为等腰三角形、等边三角形和不等边三角形; (3)三角形的两边之差大于第三边; (4)三角形按角分类应分为锐角三角形、直角三角形和钝角三角形. 其中正确的有( ) A.1个 B.2个 C.3个 D.4个3.现有两根木棒,它们的长分别为40cm和50cm,若要钉成一个三角形木架(不计接头),则在下列四根木棒中应选取( ) A.10cm B.40cm C.90cm D.100cm 4.下列长度的各组线段中,能组成三角形的是( ) A.3cm,12cm,8cm B.6cm,8cm,15cm C.2.5cm,3cm,5cm D.6.3cm,6.3cm,12.6cm5.已知一个三角形的两边长分别是3cm和4cm,则第三边长x的取值范围是____.若x是奇数,则x的值是______;这样的三角形有______个;若x是偶数,则x的值是______;这样的三角形又有________个.6.已知等腰三角形的两边长分别是3和6,则它的周长等于( ) A.12 B.12或15 C.15 D.15或187.已知三角形三边的长均为整数,其中某两条边长之差为5,若此三角形周长为奇数,则第三边长的最小值为多少?综合创新作业8.(综合题)已知a、b、c为△ABC的三边长,b、c满足(b-2)2+│c-3│=0,且a为方程│x-4│=2的解,求△ABC的周长,判断△ABC的形状.9.(创新题)已知等腰三角形的周长为8,边长为整数,求这个三角形的腰长.10.(易错题)已知等腰三角形的一边长等于4,另一边长等于9,则周长为_____.11.已知△ABC的周长为21,三边a、b、c满足关系2a-b=3,3c-2b=13,求a、b、c.
12.已知:△ABC的周长是84cm,b=6(c-a),a:c=7:8.求三边a,b,c的长。 第1题主要考察三角形的概念。第2题考察三角形的分类,仔细判断每一个命题,确保选择的准确。第3题的提示:第三边的范围应大于两边之和,小于两边之差。第4题:检查较小的两边之和是否大于第三边第5-7题是典型题,主要综合了第3题和第4题。综合创新作业比较适合有能力的同学完成,基础较差的只要掌握了当堂检测的习题就可以了。
图1
A
B
C
直角三角形
锐角三角形
斜三角形
三角形
a
A
B
C
b
c
图2
学科 数学 课题 三角形的边 课型 新课
时间 2012年 月 日 人教版 七年级下
学习目标 1.认识三角形,了解三角形的意义,认识三角形的边、内角、顶点,能用符号语言表示三角形.2.理解三角形三边不等的关系.
重点难点 三角形三边间的不等关系.用三角形三边不等关系判定三条线段可否组成三角形.
学习内容 学法及设计意图
【引入】三角形是一种最常见的几何图形之一.你能举几个例子吗?以下几个图形. 哪些是三角形 【归纳】不在一直线上三条线段首尾顺次相接组成的图形叫做三角形.图1中的三角形记作: 读作: 1、三角形的有关概念及表示(图1)(1)顶点:三角形两边的公共点称为三角形的顶点;的顶点是 , , 。(2)边:组成三角形的三条线段称为三角形的边;的三条边为 , , 。(3)内角:在三角形中,每两条边所组成的角叫做三角形的内角;的三个内角为 , , 。2:三角形的分类三角形分类有两种方法:(1)按角分类;(2)按边分类按角分类 (2)按边分类 【思考】画出一个△ABC,假设有一只小虫要从B点出发,沿三角形的边爬到C,它有几种路线可以选择 各条路线的长一样吗 三角形边的性质
(1)三角形三边关系定理及推论
定理:三角形两边的和大于第三边.推论:三角形两边的差小于第三边.
(2)表达式:△ABC中,设a>b>c
则b-c<a<b+c
a-c<b<a+c
a-b<c<a+b例题:用一条长18cm的细绳围成一个等腰三角形如果腰长的底边的2倍,那么各边的长是多少?能围成有一边的长为4cm的等腰三角形吗?为什么? 引导学生从自然景观到微型模型,从建筑物到艺术作品,甚至日常生活用品中去寻找三角形的实际例子,体现数学来源于生活。三角形的概念,学生在小学也学习过,但需进一步严格定义,教师在这里要强调“首位顺次相接”,利用上面的几个图形说明定义中增加这几个字的必要性。通过学生自学教材88页的前五段内容,独立完成空格的内容。在这里教师要强调(1) 为同一个三角形。(2)角的两边为射线,三角形的三条边为线段。自学教材88页第6段到89页探究以上文字,完成填空。按边把三角形分类时,关键是确定分类标准,这是学生学习的难点,教师要引导学生确定好分类,利用这一教学环节让学生了解和体会分类思想。“三角形两边的和大于第三边”是由“两点之间,线段最短”得到的。可根据学生的实际情况,适当引导学生回忆“几何图形”一章中学过的这个事实。“三角形两边的和大于第三边”可以用来判断三条线段能否组成三角形,要让学生体会运用这一结论解决这样的问题,一定要检查是否任意两边的和大于第三边。小窍门:检查较小的两边之和是否大于第三边在(2)中注意引导学生认真审题:“有一边的长”并没有说明这一边到底是腰还是底,要分情况讨论。
【当堂检测】1.下图中有几个三角形?用符号表示这些三角形.2.下列说法: (1)等边三角形是等腰三角形; (2)三角形按边分类可分为等腰三角形、等边三角形和不等边三角形; (3)三角形的两边之差大于第三边; (4)三角形按角分类应分为锐角三角形、直角三角形和钝角三角形. 其中正确的有( ) A.1个 B.2个 C.3个 D.4个3.现有两根木棒,它们的长分别为40cm和50cm,若要钉成一个三角形木架(不计接头),则在下列四根木棒中应选取( ) A.10cm B.40cm C.90cm D.100cm 4.下列长度的各组线段中,能组成三角形的是( ) A.3cm,12cm,8cm B.6cm,8cm,15cm C.2.5cm,3cm,5cm D.6.3cm,6.3cm,12.6cm5.已知一个三角形的两边长分别是3cm和4cm,则第三边长x的取值范围是____.若x是奇数,则x的值是______;这样的三角形有______个;若x是偶数,则x的值是______;这样的三角形又有________个.6.已知等腰三角形的两边长分别是3和6,则它的周长等于( ) A.12 B.12或15 C.15 D.15或187.已知三角形三边的长均为整数,其中某两条边长之差为5,若此三角形周长为奇数,则第三边长的最小值为多少?综合创新作业8.(综合题)已知a、b、c为△ABC的三边长,b、c满足(b-2)2+│c-3│=0,且a为方程│x-4│=2的解,求△ABC的周长,判断△ABC的形状.9.(创新题)已知等腰三角形的周长为8,边长为整数,求这个三角形的腰长.10.(易错题)已知等腰三角形的一边长等于4,另一边长等于9,则周长为_____.11.已知△ABC的周长为21,三边a、b、c满足关系2a-b=3,3c-2b=13,求a、b、c.
12.已知:△ABC的周长是84cm,b=6(c-a),a:c=7:8.求三边a,b,c的长。 第1题主要考察三角形的概念。第2题考察三角形的分类,仔细判断每一个命题,确保选择的准确。第3题的提示:第三边的范围应大于两边之和,小于两边之差。第4题:检查较小的两边之和是否大于第三边第5-7题是典型题,主要综合了第3题和第4题。综合创新作业比较适合有能力的同学完成,基础较差的只要掌握了当堂检测的习题就可以了。
图1
A
B
C
直角三角形
锐角三角形
斜三角形
三角形
a
A
B
C
b
c
图2
