人教版八年级数学下册 17.1 勾股定理的应用--最短路径问题综合题型 课件(43张)
文档属性
| 名称 | 人教版八年级数学下册 17.1 勾股定理的应用--最短路径问题综合题型 课件(43张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 11:31:11 | ||
图片预览






文档简介
(共43张PPT)
勾股定理的几何应用
—最短路径问题
知识框架
1.掌握由立体图形展开成平面图形的方法,运用建模思想构造直角三角形,利用勾股定理求最短路径问题;
2.进一步理解“在同一平面内,两点之间,线段最短”在勾股定理几何图形中的运用.
课程目标
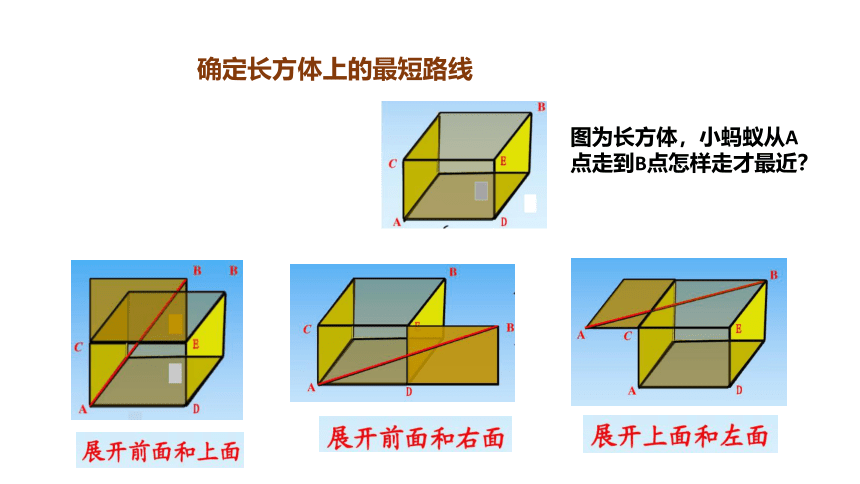
确定长方体上的最短路线
图为长方体,小蚂蚁从A点走到B点怎样走才最近?
利用长方体展开图求最短距离
如图,一只蜘蛛在一块长方体木块的一个顶点处,一只苍蝇在这个长方体的对角顶点处,若,,,问蜘蛛要沿着怎样的路线爬行,才能最快抓到苍蝇?这时蜘蛛走过的路程是多少厘米?
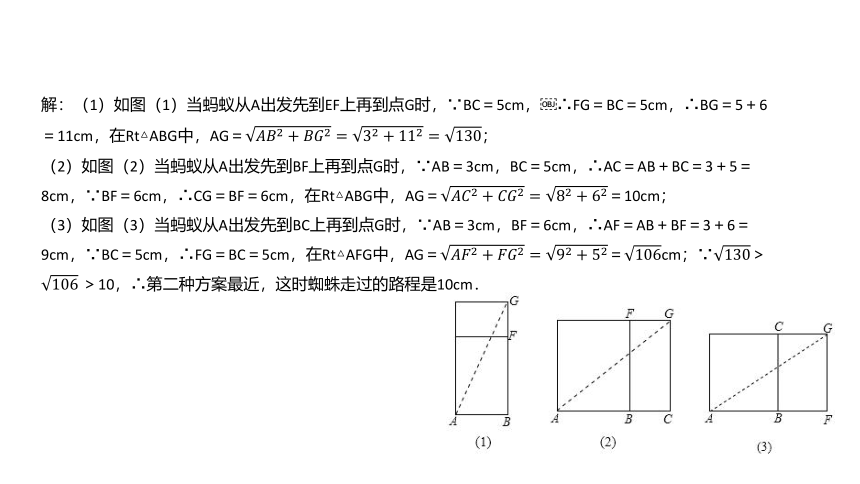
解:(1)如图(1)当蚂蚁从A出发先到EF上再到点G时,∵BC=5cm,?∴FG=BC=5cm,∴BG=5+6=11cm,在Rt△ABG中,AG=
(2)如图(2)当蚂蚁从A出发先到BF上再到点G时,∵AB=3cm,BC=5cm,∴AC=AB+BC=3+5=8cm,∵BF=6cm,∴CG=BF=6cm,在Rt△ABG中,AG==10cm;
(3)如图(3)当蚂蚁从A出发先到BC上再到点G时,∵AB=3cm,BF=6cm,∴AF=AB+BF=3+6=9cm,∵BC=5cm,∴FG=BC=5cm,在Rt△AFG中,AG==cm;∵>
>10,∴第二种方案最近,这时蜘蛛走过的路程是10cm.
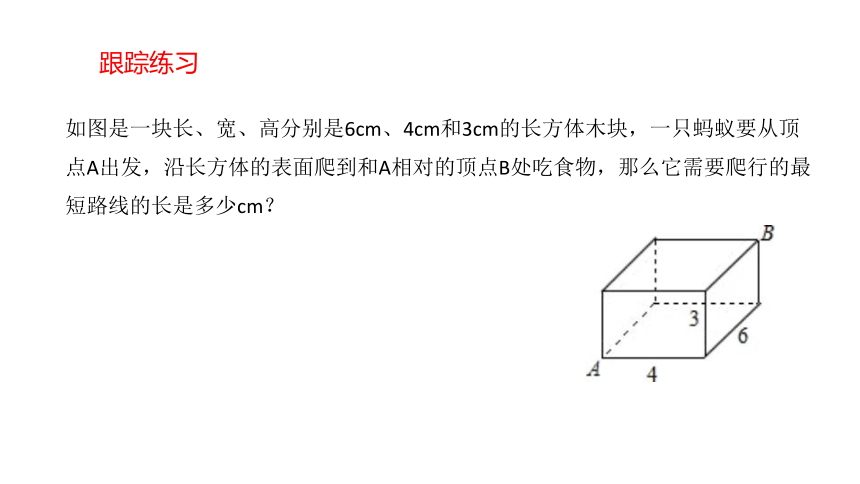
如图是一块长、宽、高分别是6cm、4cm和3cm的长方体木块,一只蚂蚁要从顶点A出发,沿长方体的表面爬到和A相对的顶点B处吃食物,那么它需要爬行的最短路线的长是多少cm?
跟踪练习
如图,一只蚂蚁在长方体木块的一个顶点处,食物在这个长方体上和蚂蚁相对的顶点处,蚂蚁急于吃到食物,所以沿着长方体的表面上向上爬,请你计算出它从处爬到处的最短路线长为多少?
跟踪练习
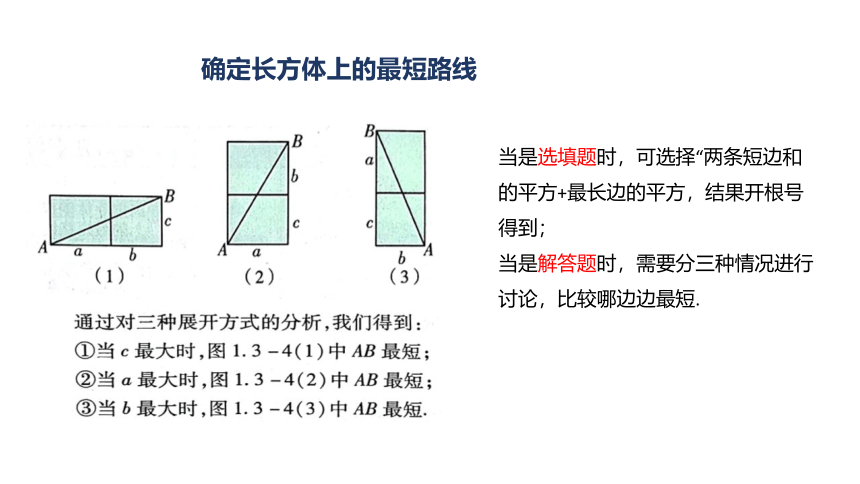
确定长方体上的最短路线
当是选填题时,可选择“两条短边和的平方+最长边的平方,结果开根号得到;
当是解答题时,需要分三种情况进行讨论,比较哪边边最短.
如图是长为5,宽为4,高为3的长方体,一只蚂蚁从顶点A沿长方体的表面爬行到顶点B的最短距离是( )
A.12
B.3
C.4
D.
跟踪练习
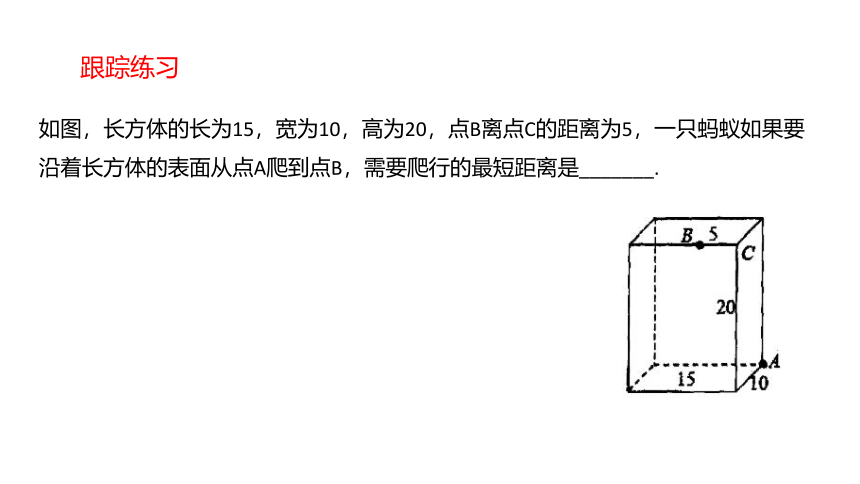
如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是_______.
跟踪练习
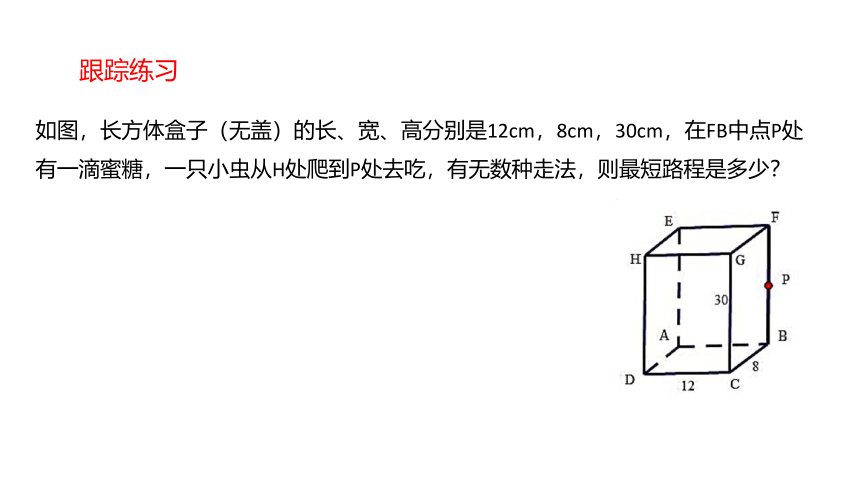
如图,长方体盒子(无盖)的长、宽、高分别是12cm,8cm,30cm,在FB中点P处有一滴蜜糖,一只小虫从H处爬到P处去吃,有无数种走法,则最短路程是多少?
跟踪练习
如图,长方体的高是9厘米,底面是边长为4厘米的正方形,一只蚂蚁沿着长方体表面从点A出发,经过3个面爬到点B,蚂蚁爬行的最短距离是多少?
跟踪练习
如图,长方体的底面边长分别为和,高为.若一只蚂蚁从点开始经过个侧面爬行一圈到达点,则蚂蚁爬行的最短路径长为(
)
A.13cm
B.12cm
C.10cm
D.8cm
跟踪练习
如图,一个上方无盖的长方体盒子紧贴地面,一只蚂蚁由盒外处出发,沿着盒子面爬行到盒内的点处,已知,,,,这只蚂蚁爬行的最短距离是________.
跟踪练习
如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60
cm,水深为AE=40
cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60
cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,则小动物爬行的最短路线长为( )
A、40
cm
B、60
cm
C、80
cm
D、100
cm
如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、3dm,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为_____dm.
确定正方体上的最短路线
图为正方体,小蚂蚁从A点走到B点怎样走才最近?
利用正方体展开图求最短距离
如图一只蚂蚁要从正方体一个顶点爬到另一个顶点,如果正方体棱长是,求最短路线长.
在棱长为厘米的正方体的一个顶点处,有只蚂蚁,现要向顶点处爬行,已知蚂蚁的爬行速度每秒厘米蚂蚁,能否在秒内从点爬到点?
如图是一个棱长为的正方体盒子,一只蚂蚁从棱上的中点出发,沿盒的表面爬到棱上后,接着又沿盒子的表面爬到盒底的处,那么,整个爬行中,蚂蚁要爬行的最短路程为________.
B
A
C
A
C
B
B’
图为圆柱体,小蚂蚁从A点走到B点怎样走才最近?
确定圆柱上的最短路线
易错点:
圆柱展开为底面圆周长(或倍数关系),而非直径或半径,找点的位置时,注意是走半个底面圆周长,还是整个底面圆周长。
化“立体”为“平面”,将求立体图形上两点间的距离转化为求平面内两点间的距离.
利用圆柱展开图直接求最短距离
如图,一圆柱高,底面周长为,一只蚂蚁从点爬到点处吃食,要爬行的最短路程是(
)
A..8
B.10
C.12
D.20
例题讲解
展:如图展开是一个长方形,长方形的长为圆柱的底面周长等于12cm,半个底面圆周长为6cm,长方形的宽为圆柱体的高等于8cm;
找:找点A、点B;
连:连接AB,过B点往对边作垂线交于点C;
算:在Rt△ACB中,AB==
=10cm;
答:爬行的最短路径为10cm,故选B.
如图,有一个圆柱,它的高等于,底面半径等干,在圆柱下底面的点有一只壁虎,它想吃到上底面上与点相对的点处的食物,需要爬行的最短路程是________.取
跟踪练习
有一圆形油罐底面圆的周长是,高,一只蚂蚁从距底面到的对角处吃食物,它爬行的最短路线长为多少.
跟踪练习
如图,有一圆柱油罐,已知油罐的底面圆的周长是米,高是米,要从点起环绕油罐建梯子,梯子的顶端正好到达点的正上方点,则梯子最短需多长?
跟踪练习
有一圆柱形油罐,如图所示,要从A点环绕油罐建梯子到B点,正好B点在A点的正上方,已知油罐的周长为12m,高AB为5m,问:所建梯子最短需多少米?
跟踪练习
求多圈最短距离
为了庆祝国庆,学校准备在教学楼大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为,高为.如果要求彩带从柱子底端的处绕柱子圈后到达柱子顶端的处,那么至少应购买彩带________米.
解:将圆柱表面切开展开呈长方形,则有螺旋线长为四个长方形并排后的长方形的对角线长,
∵
圆柱高,底面周长,
,
所以,彩带长至少是.
故答案为:.
求多圈最短距离,可采用两种方法:
①先求多圈之后的底面周长,和高构成直角三角形,求斜边长;
②先求一圈的底面周长,和一圈的高构成直角三角形求斜边长,再乘以圈数,得到总斜边长.
如图,为了庆祝“五?一”,学校准备在教学大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为,高为.如果要求彩带从柱子底端的处均匀地绕柱子圈后到达柱子顶端的处(线段与地面垂直),那么应购买彩带的长度为_______
.
跟踪练习
如图,圆柱底面圆的半径为,高为,点,分别是圆柱两底面圆周上的点,且,在同一母线上,用一根棉线从点顺着圆柱侧面绕圈到点,那么这根棉线的长度最短是多少?
跟踪练习
如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为尺,底面周长为尺,有葛藤自点处缠绕而上,绕五周后其末端恰好到达点处,则问题中葛藤的最短长度是________尺.
跟踪练习
求由外到内最短距离
如图,圆柱形玻璃板,高为,底面周长为,在杯内离杯底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的处,则蚂蚁到达蜂蜜的最短距离
.
A.14
B.15
C.16
D.17
解:沿过A的圆柱的高剪开,得出矩形EFGH,过C作CQ⊥EF于Q,作A关于EH的对称点A′,连接A′C交EH于P,连接AP,则AP+PC就是蚂蚁到达蜂蜜的最短距离,∵AE=A′E,A′P=AP,∴AP+PC=A′P+PC=A′C,∵CQ=12×18cm=9cm,A′Q=12cm?4cm+4cm=12cm,在Rt△A′QC中,由勾股定理得:A′C==15cm,故选:B.
由外到内最短距离,其实是指两条线段和最短,牵扯到将军饮马问题,需要做点关于直线的对称点,运用到“两点之间线段最短”的知识.
结论:PA+PB的最小值为线段AB'的长度;
关键点:构造对称,转换线段,利用两点之间线段最短确定所求点位置.
如图,圆柱形容器高为,底面周长为.在容器内壁距离容器底部的点处有一蚊子,此时一只壁虎正好在容器外壁,距离容器上沿与蚊子相对的点处,则壁虎捕捉蚊子需爬行的最短距离为________(不计壁厚).
跟踪练习
解题步骤:展—找—连—算—答
注意点:
长方体:展开不同的两面,得到的长方形的长和宽不相同,所以要通过比较才能得出最短路径.
正方体:因为每个面的大小相同,展开后长方形的长宽不变,所以结果相同。
圆柱体:圆柱体的展开图是一个长方形,但需要注意展开后点的位置的确定;
课堂小结
勾股定理的几何应用
—最短路径问题
知识框架
1.掌握由立体图形展开成平面图形的方法,运用建模思想构造直角三角形,利用勾股定理求最短路径问题;
2.进一步理解“在同一平面内,两点之间,线段最短”在勾股定理几何图形中的运用.
课程目标
确定长方体上的最短路线
图为长方体,小蚂蚁从A点走到B点怎样走才最近?
利用长方体展开图求最短距离
如图,一只蜘蛛在一块长方体木块的一个顶点处,一只苍蝇在这个长方体的对角顶点处,若,,,问蜘蛛要沿着怎样的路线爬行,才能最快抓到苍蝇?这时蜘蛛走过的路程是多少厘米?
解:(1)如图(1)当蚂蚁从A出发先到EF上再到点G时,∵BC=5cm,?∴FG=BC=5cm,∴BG=5+6=11cm,在Rt△ABG中,AG=
(2)如图(2)当蚂蚁从A出发先到BF上再到点G时,∵AB=3cm,BC=5cm,∴AC=AB+BC=3+5=8cm,∵BF=6cm,∴CG=BF=6cm,在Rt△ABG中,AG==10cm;
(3)如图(3)当蚂蚁从A出发先到BC上再到点G时,∵AB=3cm,BF=6cm,∴AF=AB+BF=3+6=9cm,∵BC=5cm,∴FG=BC=5cm,在Rt△AFG中,AG==cm;∵>
>10,∴第二种方案最近,这时蜘蛛走过的路程是10cm.
如图是一块长、宽、高分别是6cm、4cm和3cm的长方体木块,一只蚂蚁要从顶点A出发,沿长方体的表面爬到和A相对的顶点B处吃食物,那么它需要爬行的最短路线的长是多少cm?
跟踪练习
如图,一只蚂蚁在长方体木块的一个顶点处,食物在这个长方体上和蚂蚁相对的顶点处,蚂蚁急于吃到食物,所以沿着长方体的表面上向上爬,请你计算出它从处爬到处的最短路线长为多少?
跟踪练习
确定长方体上的最短路线
当是选填题时,可选择“两条短边和的平方+最长边的平方,结果开根号得到;
当是解答题时,需要分三种情况进行讨论,比较哪边边最短.
如图是长为5,宽为4,高为3的长方体,一只蚂蚁从顶点A沿长方体的表面爬行到顶点B的最短距离是( )
A.12
B.3
C.4
D.
跟踪练习
如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是_______.
跟踪练习
如图,长方体盒子(无盖)的长、宽、高分别是12cm,8cm,30cm,在FB中点P处有一滴蜜糖,一只小虫从H处爬到P处去吃,有无数种走法,则最短路程是多少?
跟踪练习
如图,长方体的高是9厘米,底面是边长为4厘米的正方形,一只蚂蚁沿着长方体表面从点A出发,经过3个面爬到点B,蚂蚁爬行的最短距离是多少?
跟踪练习
如图,长方体的底面边长分别为和,高为.若一只蚂蚁从点开始经过个侧面爬行一圈到达点,则蚂蚁爬行的最短路径长为(
)
A.13cm
B.12cm
C.10cm
D.8cm
跟踪练习
如图,一个上方无盖的长方体盒子紧贴地面,一只蚂蚁由盒外处出发,沿着盒子面爬行到盒内的点处,已知,,,,这只蚂蚁爬行的最短距离是________.
跟踪练习
如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60
cm,水深为AE=40
cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60
cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,则小动物爬行的最短路线长为( )
A、40
cm
B、60
cm
C、80
cm
D、100
cm
如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、3dm,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为_____dm.
确定正方体上的最短路线
图为正方体,小蚂蚁从A点走到B点怎样走才最近?
利用正方体展开图求最短距离
如图一只蚂蚁要从正方体一个顶点爬到另一个顶点,如果正方体棱长是,求最短路线长.
在棱长为厘米的正方体的一个顶点处,有只蚂蚁,现要向顶点处爬行,已知蚂蚁的爬行速度每秒厘米蚂蚁,能否在秒内从点爬到点?
如图是一个棱长为的正方体盒子,一只蚂蚁从棱上的中点出发,沿盒的表面爬到棱上后,接着又沿盒子的表面爬到盒底的处,那么,整个爬行中,蚂蚁要爬行的最短路程为________.
B
A
C
A
C
B
B’
图为圆柱体,小蚂蚁从A点走到B点怎样走才最近?
确定圆柱上的最短路线
易错点:
圆柱展开为底面圆周长(或倍数关系),而非直径或半径,找点的位置时,注意是走半个底面圆周长,还是整个底面圆周长。
化“立体”为“平面”,将求立体图形上两点间的距离转化为求平面内两点间的距离.
利用圆柱展开图直接求最短距离
如图,一圆柱高,底面周长为,一只蚂蚁从点爬到点处吃食,要爬行的最短路程是(
)
A..8
B.10
C.12
D.20
例题讲解
展:如图展开是一个长方形,长方形的长为圆柱的底面周长等于12cm,半个底面圆周长为6cm,长方形的宽为圆柱体的高等于8cm;
找:找点A、点B;
连:连接AB,过B点往对边作垂线交于点C;
算:在Rt△ACB中,AB==
=10cm;
答:爬行的最短路径为10cm,故选B.
如图,有一个圆柱,它的高等于,底面半径等干,在圆柱下底面的点有一只壁虎,它想吃到上底面上与点相对的点处的食物,需要爬行的最短路程是________.取
跟踪练习
有一圆形油罐底面圆的周长是,高,一只蚂蚁从距底面到的对角处吃食物,它爬行的最短路线长为多少.
跟踪练习
如图,有一圆柱油罐,已知油罐的底面圆的周长是米,高是米,要从点起环绕油罐建梯子,梯子的顶端正好到达点的正上方点,则梯子最短需多长?
跟踪练习
有一圆柱形油罐,如图所示,要从A点环绕油罐建梯子到B点,正好B点在A点的正上方,已知油罐的周长为12m,高AB为5m,问:所建梯子最短需多少米?
跟踪练习
求多圈最短距离
为了庆祝国庆,学校准备在教学楼大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为,高为.如果要求彩带从柱子底端的处绕柱子圈后到达柱子顶端的处,那么至少应购买彩带________米.
解:将圆柱表面切开展开呈长方形,则有螺旋线长为四个长方形并排后的长方形的对角线长,
∵
圆柱高,底面周长,
,
所以,彩带长至少是.
故答案为:.
求多圈最短距离,可采用两种方法:
①先求多圈之后的底面周长,和高构成直角三角形,求斜边长;
②先求一圈的底面周长,和一圈的高构成直角三角形求斜边长,再乘以圈数,得到总斜边长.
如图,为了庆祝“五?一”,学校准备在教学大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为,高为.如果要求彩带从柱子底端的处均匀地绕柱子圈后到达柱子顶端的处(线段与地面垂直),那么应购买彩带的长度为_______
.
跟踪练习
如图,圆柱底面圆的半径为,高为,点,分别是圆柱两底面圆周上的点,且,在同一母线上,用一根棉线从点顺着圆柱侧面绕圈到点,那么这根棉线的长度最短是多少?
跟踪练习
如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为尺,底面周长为尺,有葛藤自点处缠绕而上,绕五周后其末端恰好到达点处,则问题中葛藤的最短长度是________尺.
跟踪练习
求由外到内最短距离
如图,圆柱形玻璃板,高为,底面周长为,在杯内离杯底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的处,则蚂蚁到达蜂蜜的最短距离
.
A.14
B.15
C.16
D.17
解:沿过A的圆柱的高剪开,得出矩形EFGH,过C作CQ⊥EF于Q,作A关于EH的对称点A′,连接A′C交EH于P,连接AP,则AP+PC就是蚂蚁到达蜂蜜的最短距离,∵AE=A′E,A′P=AP,∴AP+PC=A′P+PC=A′C,∵CQ=12×18cm=9cm,A′Q=12cm?4cm+4cm=12cm,在Rt△A′QC中,由勾股定理得:A′C==15cm,故选:B.
由外到内最短距离,其实是指两条线段和最短,牵扯到将军饮马问题,需要做点关于直线的对称点,运用到“两点之间线段最短”的知识.
结论:PA+PB的最小值为线段AB'的长度;
关键点:构造对称,转换线段,利用两点之间线段最短确定所求点位置.
如图,圆柱形容器高为,底面周长为.在容器内壁距离容器底部的点处有一蚊子,此时一只壁虎正好在容器外壁,距离容器上沿与蚊子相对的点处,则壁虎捕捉蚊子需爬行的最短距离为________(不计壁厚).
跟踪练习
解题步骤:展—找—连—算—答
注意点:
长方体:展开不同的两面,得到的长方形的长和宽不相同,所以要通过比较才能得出最短路径.
正方体:因为每个面的大小相同,展开后长方形的长宽不变,所以结果相同。
圆柱体:圆柱体的展开图是一个长方形,但需要注意展开后点的位置的确定;
课堂小结
