2020-2021学年湘教版八年级下册2.5.1矩形的性质课件(22张)
文档属性
| 名称 | 2020-2021学年湘教版八年级下册2.5.1矩形的性质课件(22张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 00:00:00 | ||
图片预览




文档简介
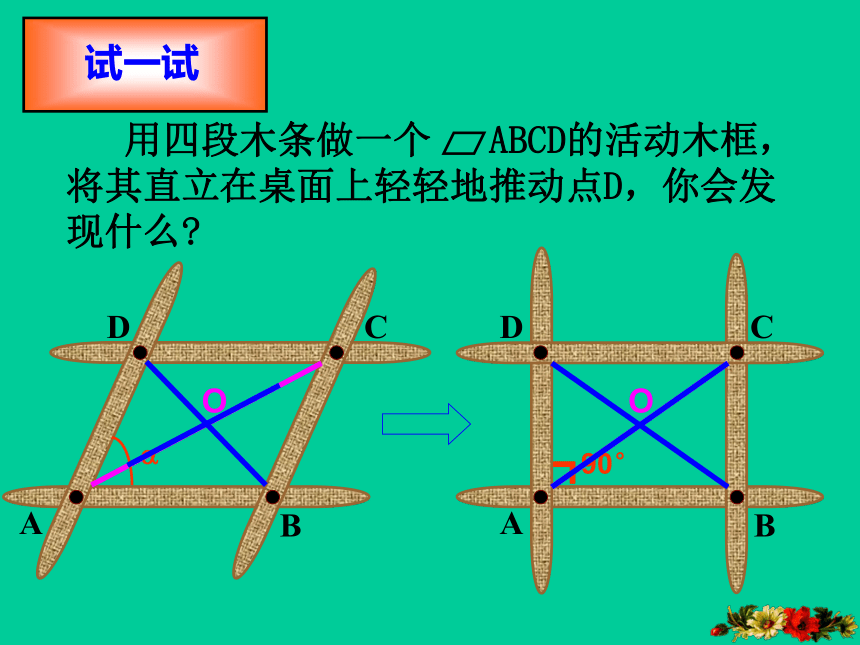
用四段木条做一个 ABCD的活动木框,将其直立在桌面上轻轻地推动点D,你会发现什么?
试一试
D
A
C
B
D
A
C
B
?
O
O
┓
90°
A
B
C
D
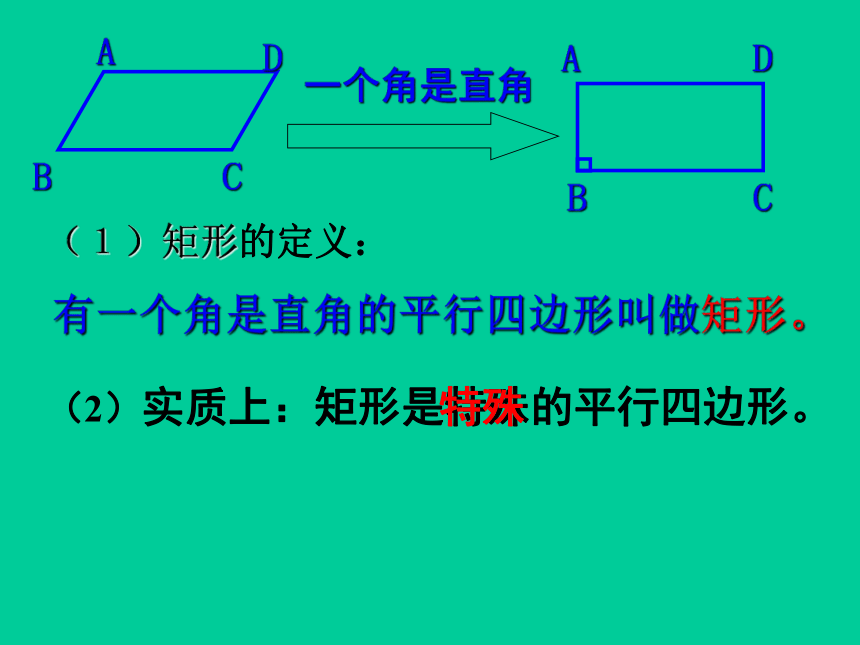
有一个角是直角的平行四边形叫做矩形。
A
B
C
D
(1)矩形的定义:
(2)实质上:矩形是特殊的平行四边形。
特殊
一个角是直角
小学里学过的长方形、正方形都是矩形
想一想:
你能举出在人们的日常生活和生产实践中,有哪些东西是矩形的?
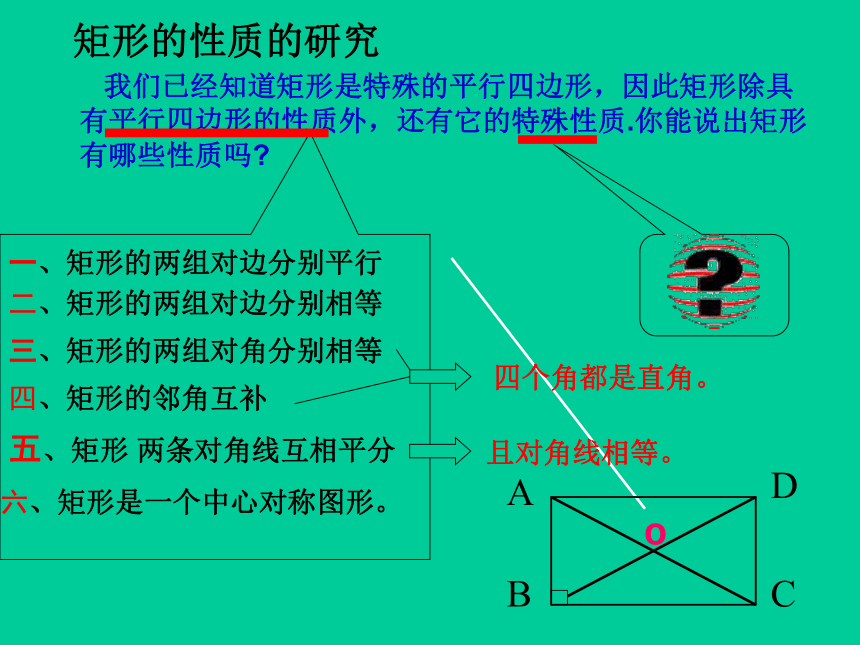
矩形的性质的研究
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗?
五、矩形 两条对角线互相平分
三、矩形的两组对角分别相等
二、矩形的两组对边分别相等
一、矩形的两组对边分别平行
四、矩形的邻角互补
六、矩形是一个中心对称图形。
四个角都是直角。
且对角线相等。
O
A
B
C
D
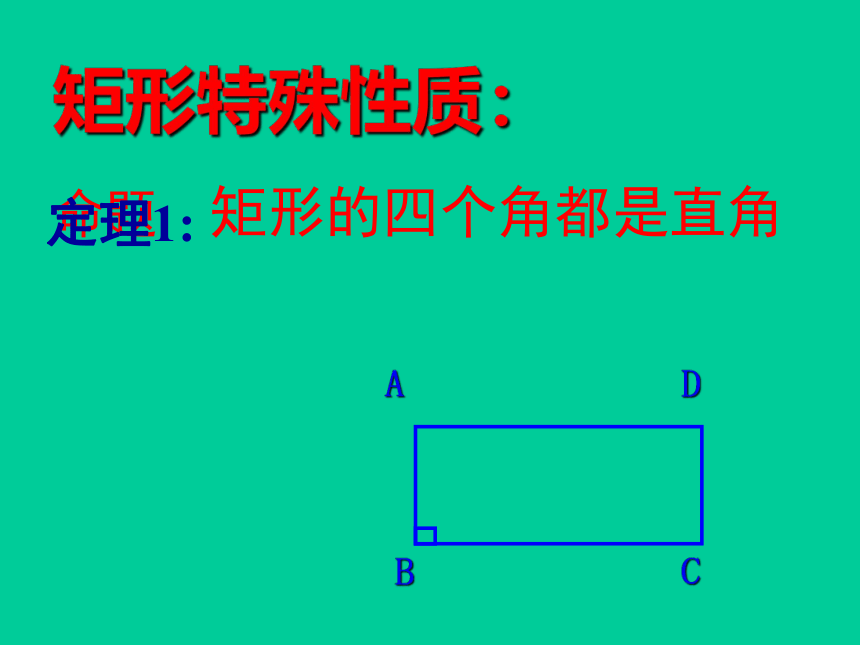
矩形特殊性质:
A
B
C
D
命题 矩形的四个角都是直角
定理1:
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
返回
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD
命题 矩形的对角线相等.
定理2:
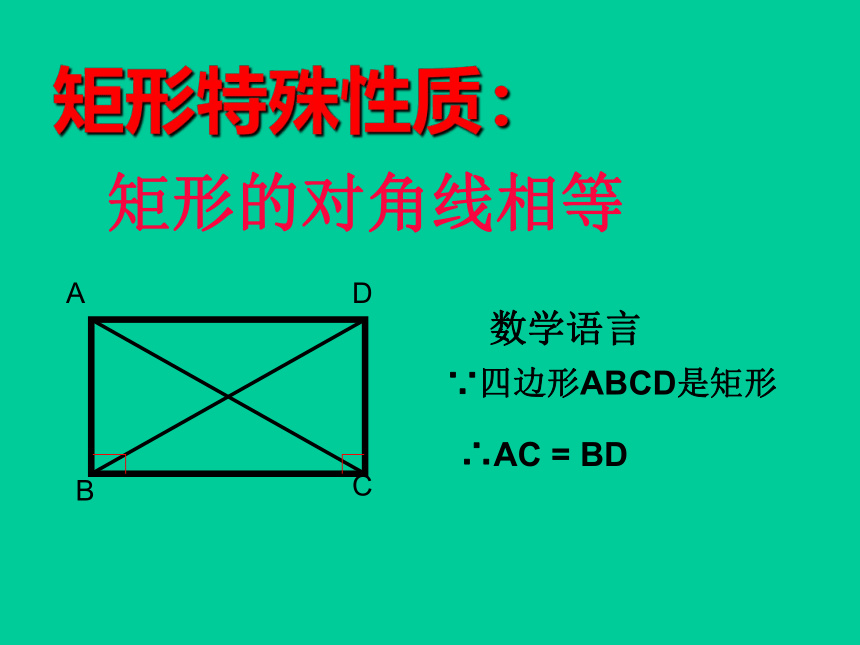
矩形的对角线相等
数学语言
∵四边形ABCD是矩形
∴AC = BD
矩形特殊性质:
A
B
C
D
如图,矩形ABCD中,对角线AC、BD相交于点O,请探讨OC与BD的关系
矩形ABCD的对角线AC、BD相交于点O,图中有多少个直角三角形?有多少个等腰三角形? 有多少对全等三角形?
矩形 问题
直角三角形和等腰三角形 问题
转化
A
B
C
D
O
A
B
C
D
O
探索矩形的对称性:
矩形是中心对称图形,又是轴对称图形
想一想
矩形是轴对称图形吗?对称轴有几条?
是中心对称图形吗?
矩形的 两条对角线互相平分
矩形的两组对边分别平行
矩形的两组对边分别相等
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
数学语言
∵四边形ABCD是矩形
∴AD = BC ,CD = AB
∴AD ∥BC ,CD ∥AB
∴AC= BD
A
B
C
D
O
∴AO= CO ,OD = OB
矩形既是中心对称图形,又是
轴对称图形。
对称性
4.下列性质中,矩形不一定具有的是( )
A、对角线相等 B、 四个角都相等
C、对角线垂直 D、是轴对称图形
1.矩形的定义中有两个条件:一是____________,二是_________________。
2.有一个角是直角的四边形是矩形。( )
3.矩形的对角线互相平分。( )
平行四边形
有一个角是直角
√
×
C
5.矩形具有而平行四边形不具有的性质是( ) A 两组对边分别平行 B 对角相等
C 对角线互相平分 D 对角线相等
6.矩形ABCD中,对角线AC、BD把矩形分成( )个等腰三角形,( )个直角三角形。
(A)2 (B)4 (C)6 (D)8
D
B
B
O
A
B
D
C
例: 已知:矩形ABCD的两条对角线AC、BD相交于点0, AC = 4cm, ∠AOB=60°,
求BC的长。
A
B
C
D
O
例: 已知:矩形ABCD的两条对角线AC、BD相交于点0, ∠AOD=120°, AB = 4cm,
求(1)判断△AOB的形状;
(2)矩形对角线的长.
B
C
D
120°
O
4
A
练一练
在矩形ABCD中,对角线AC与BD相交于点O,已知AB=6,BC=8,
(1)求AC= —,BD= —,
(2)矩形ABCD的周长是= —,面积是= —。
A
B
C
D
O
10
10
28
48
6
8
已知:如图,过矩形ABCD的顶点作CE//BD,交AB的延长线于E。
求证:∠CAE=∠CEA
A
B
C
D
E
相信你,一定行
如图,将矩形纸片ABCD沿对角线BD对折,使点A落在点E处,BE交CD于点F。已知∠ABD=30度.
求∠CDE的度数;
求证:EF=FC
A
B
C
D
E
F
矩形的四个角都是直角.
※ 矩形的性质定理1
矩形的对角线相等.
※ 矩形的性质定理2
矩形定义:
有一个角是直角的平行四边形叫做矩形.
※ 矩形的对称性
矩形是中心对称图形,
又是轴对称图形
这节课你学到了什么? 还有什么困惑吗?
已知:如图,在矩形ABCD中,M为BC的中点.
求证:
(2)若要使∠AMD是直角,应添加什
么条件?
(1)AM=DM.
试一试
D
A
C
B
D
A
C
B
?
O
O
┓
90°
A
B
C
D
有一个角是直角的平行四边形叫做矩形。
A
B
C
D
(1)矩形的定义:
(2)实质上:矩形是特殊的平行四边形。
特殊
一个角是直角
小学里学过的长方形、正方形都是矩形
想一想:
你能举出在人们的日常生活和生产实践中,有哪些东西是矩形的?
矩形的性质的研究
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗?
五、矩形 两条对角线互相平分
三、矩形的两组对角分别相等
二、矩形的两组对边分别相等
一、矩形的两组对边分别平行
四、矩形的邻角互补
六、矩形是一个中心对称图形。
四个角都是直角。
且对角线相等。
O
A
B
C
D
矩形特殊性质:
A
B
C
D
命题 矩形的四个角都是直角
定理1:
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
返回
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD
命题 矩形的对角线相等.
定理2:
矩形的对角线相等
数学语言
∵四边形ABCD是矩形
∴AC = BD
矩形特殊性质:
A
B
C
D
如图,矩形ABCD中,对角线AC、BD相交于点O,请探讨OC与BD的关系
矩形ABCD的对角线AC、BD相交于点O,图中有多少个直角三角形?有多少个等腰三角形? 有多少对全等三角形?
矩形 问题
直角三角形和等腰三角形 问题
转化
A
B
C
D
O
A
B
C
D
O
探索矩形的对称性:
矩形是中心对称图形,又是轴对称图形
想一想
矩形是轴对称图形吗?对称轴有几条?
是中心对称图形吗?
矩形的 两条对角线互相平分
矩形的两组对边分别平行
矩形的两组对边分别相等
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
数学语言
∵四边形ABCD是矩形
∴AD = BC ,CD = AB
∴AD ∥BC ,CD ∥AB
∴AC= BD
A
B
C
D
O
∴AO= CO ,OD = OB
矩形既是中心对称图形,又是
轴对称图形。
对称性
4.下列性质中,矩形不一定具有的是( )
A、对角线相等 B、 四个角都相等
C、对角线垂直 D、是轴对称图形
1.矩形的定义中有两个条件:一是____________,二是_________________。
2.有一个角是直角的四边形是矩形。( )
3.矩形的对角线互相平分。( )
平行四边形
有一个角是直角
√
×
C
5.矩形具有而平行四边形不具有的性质是( ) A 两组对边分别平行 B 对角相等
C 对角线互相平分 D 对角线相等
6.矩形ABCD中,对角线AC、BD把矩形分成( )个等腰三角形,( )个直角三角形。
(A)2 (B)4 (C)6 (D)8
D
B
B
O
A
B
D
C
例: 已知:矩形ABCD的两条对角线AC、BD相交于点0, AC = 4cm, ∠AOB=60°,
求BC的长。
A
B
C
D
O
例: 已知:矩形ABCD的两条对角线AC、BD相交于点0, ∠AOD=120°, AB = 4cm,
求(1)判断△AOB的形状;
(2)矩形对角线的长.
B
C
D
120°
O
4
A
练一练
在矩形ABCD中,对角线AC与BD相交于点O,已知AB=6,BC=8,
(1)求AC= —,BD= —,
(2)矩形ABCD的周长是= —,面积是= —。
A
B
C
D
O
10
10
28
48
6
8
已知:如图,过矩形ABCD的顶点作CE//BD,交AB的延长线于E。
求证:∠CAE=∠CEA
A
B
C
D
E
相信你,一定行
如图,将矩形纸片ABCD沿对角线BD对折,使点A落在点E处,BE交CD于点F。已知∠ABD=30度.
求∠CDE的度数;
求证:EF=FC
A
B
C
D
E
F
矩形的四个角都是直角.
※ 矩形的性质定理1
矩形的对角线相等.
※ 矩形的性质定理2
矩形定义:
有一个角是直角的平行四边形叫做矩形.
※ 矩形的对称性
矩形是中心对称图形,
又是轴对称图形
这节课你学到了什么? 还有什么困惑吗?
已知:如图,在矩形ABCD中,M为BC的中点.
求证:
(2)若要使∠AMD是直角,应添加什
么条件?
(1)AM=DM.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
