北京市丰台区2020-2021学年高二下学期期中联考数学试题(A卷) Word版含答案
文档属性
| 名称 | 北京市丰台区2020-2021学年高二下学期期中联考数学试题(A卷) Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 500.5KB | ||
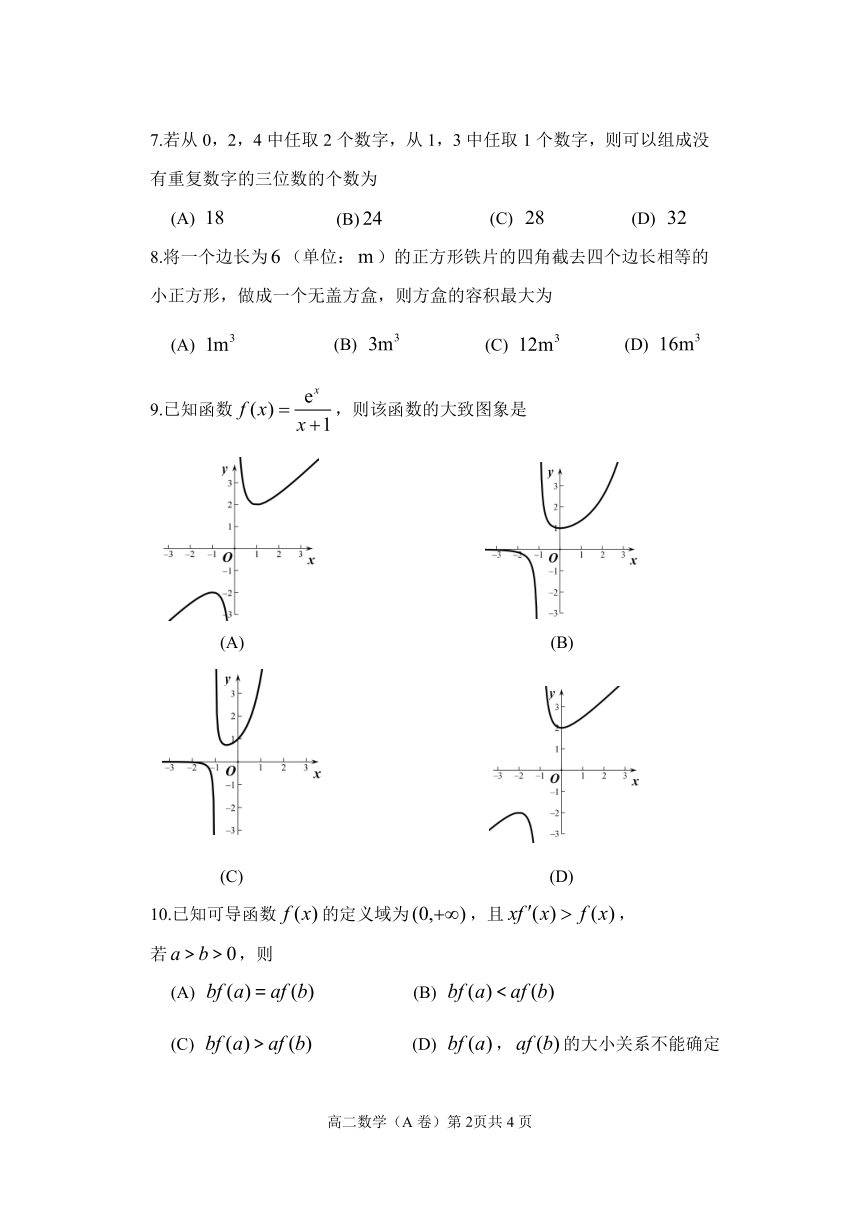
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 00:00:00 | ||
图片预览



文档简介
丰台区2020-2021学年度第二学期期中考试联考
高二数学(A卷)考试时间:90分钟
第I卷(选择题共40分)
一、选择题(每小题4分,共40分.在每小题给出的四个选项中,只有一个选项是正确的.)
1.已知函数,那么函数在处的导数为
(A) (B) (C) (D)
2.某质点沿直线运动,位移(单位:)与时间(单位:)之间的关系为,则质点在时的瞬时速度为
(A)8 (B) 12 (C) 18 (D)24
3.甲、乙、丙、丁4名同学和1名老师站成一排合影留念,要求老师必须站在中间,则不同站法种数为
(A) (B) (C) (D)
4.在的展开式中,各项系数的和是
(A) (B) (C) (D)
5.将封不同的信分别投入到个信箱中,则不同的投送方式的种数为
(A) (B) (C) (D)
6.已知函数的图象如图所示,那么下列各式正确的是
(A)
(B)
(C)
(D)
7.若从0,2,4中任取2个数字,从1,3中任取1个数字,则可以组成没有重复数字的三位数的个数为
(A) (B) (C) (D)
8.将一个边长为(单位:)的正方形铁片的四角截去四个边长相等的小正方形,做成一个无盖方盒,则方盒的容积最大为
(A) (B) (C) (D)
9.已知函数,则该函数的大致图象是
(A) (B)
(C) (D)
10.已知可导函数的定义域为,且,
若,则
(A) (B)
(C) (D) ,的大小关系不能确定
第Ⅱ卷(非选择题共60分)
二、填空题(每小题4分,共24分.)
11.在平面直角坐标系中,点的横坐标在集合内取值,纵坐标在集合内取值,则不同的点共有_____个.
12.在的展开式中,常数项为_____.
13.在的展开式中,的系数为,则_____.
14.现要从抗击疫情的名志愿者中选名志愿者,分别承担“防疫宣传讲解”、“站岗执勤”和“发放口罩”三项工作,其中志愿者甲不能承担“防疫宣传讲解”工作,则不同的选法有_____种.(结果用数字作答)
15.已知直线是曲线的切线,则的值为_____.
16.已知函数.
(1)若,则函数的单调递减区间为_____;
(2)若在区间上恒成立,则实数的取值范围是_____.
三、解答题(共36分,解答应写出文字说明、演算步骤或证明过程.)
17.(本小题9分)
已知函数.
(Ⅰ)求曲线在点处的切线方程;
(Ⅱ)求函数的极值.
(本小题6分)
某学校为普及2022年北京冬奥会知识,现从4名男同学和2名女同
学中选出3名同学担任宣讲员.
(Ⅰ)共有多少种不同选法?(结果用数字作答)
(Ⅱ)如果至少有1名女同学参加,且这3名同学分别在周五、周六
和周日进行宣讲,那么共有多少种不同选法?(结果用数字作答)
19.(本小题9分)
已知函数在处有极值2.
(Ⅰ)求的值;
(Ⅱ)证明:.
20.(本小题12分)
已知函数.
(Ⅰ)讨论函数的单调性;
(Ⅱ)求出函数零点的个数.
丰台区2020—2021学年度第二学期期中联考
高二数学A卷参考答案
第Ⅰ卷(选择题,每小题4分,共40分.)
题号 1 2 3 4 5 6 7 8 9 10
答案
第Ⅱ卷(非选择题 共60分)
二.填空题(每题4分,共24分,其中第16题每空2分.)
11. 4 12. 20 13. 5 14. 48
15. 16(1) (2)
注:16题第一空,均正确.
三.解答题(共36分.)
17.解:(Ⅰ), , ...............1分
则,且, ...............3分
所以,,
即. ...............4分
(Ⅱ)令,解得,或 ..........5分
当变化时,,的变化情况如下表所示:
单调递增
单调递减
单调递增
............7分
因此,当时,有极大值,并且极大值为
;
当时,有极小值,并且极小值为
................9分
18.解:(Ⅰ)所有不同选法种数,就是从6名同学中抽出3名的组合数,
所以选法种数为
; ................2分
(Ⅱ)从6名同学抽出的3名中至少有1名女同学,包括1名女同学2
名男同学和2名女同学1名男同学两种情况,所以选法种数为
, ................4分
又这3名同学分别在周五、周六、周日进行宣讲,
所以选法种数为
.....6分
19.解:(Ⅰ),,由已知可得, ........1分
,即, ........2分
所以, ........3分
经检验符合题意,所以 ........4分
(Ⅱ)原不等式转化为,
设,那么,........5分
令, 解得.
当变化时,,的变化情况如下表所示:
单调递减
单调递增
................6分
所以,当时,取得最小值.
所以, ................8分
即,
所以. ................9分
20.解:(Ⅰ)函数的定义域为,
...........2分
①当时,,所以在上单调递增; ...3分
②当时,,解得.
当变化时,,的变化情况如下表所示:
单调递减
单调递增
所以,在上单调递减,在单调递增. ...........5分
综上:当时,在上单调递增;
当时,在上单调递减,在上单调递增.
(Ⅱ)当时,在上单调递增,且,
所以有一个零点;
当时,由(Ⅰ)知,在上单调递增,
且,,
所以存在唯一,使得,
所以有一个零点;
当时,由(Ⅰ)知,在上单调递减,
在上单调递增,所以,则
①,即,,
所以没有零点;
②,即,,
当时,,
所以有一个零点;
③,即,此时,
一方面,,又在上单调递增,
所以存在唯一,使得;
另一方面,,取,则,
令,则,
由于,所以,在单调递减.
所以,.
由于在上单调递减,且,,
所以存在唯一,使得,
所以,当时,在有两个零点.
综上:或,有个零点;
,有个零点;
,有个零点. ..............12分
(其他解法,酌情给分.)
高二数学(A卷)第9页共4页
高二数学(A卷)考试时间:90分钟
第I卷(选择题共40分)
一、选择题(每小题4分,共40分.在每小题给出的四个选项中,只有一个选项是正确的.)
1.已知函数,那么函数在处的导数为
(A) (B) (C) (D)
2.某质点沿直线运动,位移(单位:)与时间(单位:)之间的关系为,则质点在时的瞬时速度为
(A)8 (B) 12 (C) 18 (D)24
3.甲、乙、丙、丁4名同学和1名老师站成一排合影留念,要求老师必须站在中间,则不同站法种数为
(A) (B) (C) (D)
4.在的展开式中,各项系数的和是
(A) (B) (C) (D)
5.将封不同的信分别投入到个信箱中,则不同的投送方式的种数为
(A) (B) (C) (D)
6.已知函数的图象如图所示,那么下列各式正确的是
(A)
(B)
(C)
(D)
7.若从0,2,4中任取2个数字,从1,3中任取1个数字,则可以组成没有重复数字的三位数的个数为
(A) (B) (C) (D)
8.将一个边长为(单位:)的正方形铁片的四角截去四个边长相等的小正方形,做成一个无盖方盒,则方盒的容积最大为
(A) (B) (C) (D)
9.已知函数,则该函数的大致图象是
(A) (B)
(C) (D)
10.已知可导函数的定义域为,且,
若,则
(A) (B)
(C) (D) ,的大小关系不能确定
第Ⅱ卷(非选择题共60分)
二、填空题(每小题4分,共24分.)
11.在平面直角坐标系中,点的横坐标在集合内取值,纵坐标在集合内取值,则不同的点共有_____个.
12.在的展开式中,常数项为_____.
13.在的展开式中,的系数为,则_____.
14.现要从抗击疫情的名志愿者中选名志愿者,分别承担“防疫宣传讲解”、“站岗执勤”和“发放口罩”三项工作,其中志愿者甲不能承担“防疫宣传讲解”工作,则不同的选法有_____种.(结果用数字作答)
15.已知直线是曲线的切线,则的值为_____.
16.已知函数.
(1)若,则函数的单调递减区间为_____;
(2)若在区间上恒成立,则实数的取值范围是_____.
三、解答题(共36分,解答应写出文字说明、演算步骤或证明过程.)
17.(本小题9分)
已知函数.
(Ⅰ)求曲线在点处的切线方程;
(Ⅱ)求函数的极值.
(本小题6分)
某学校为普及2022年北京冬奥会知识,现从4名男同学和2名女同
学中选出3名同学担任宣讲员.
(Ⅰ)共有多少种不同选法?(结果用数字作答)
(Ⅱ)如果至少有1名女同学参加,且这3名同学分别在周五、周六
和周日进行宣讲,那么共有多少种不同选法?(结果用数字作答)
19.(本小题9分)
已知函数在处有极值2.
(Ⅰ)求的值;
(Ⅱ)证明:.
20.(本小题12分)
已知函数.
(Ⅰ)讨论函数的单调性;
(Ⅱ)求出函数零点的个数.
丰台区2020—2021学年度第二学期期中联考
高二数学A卷参考答案
第Ⅰ卷(选择题,每小题4分,共40分.)
题号 1 2 3 4 5 6 7 8 9 10
答案
第Ⅱ卷(非选择题 共60分)
二.填空题(每题4分,共24分,其中第16题每空2分.)
11. 4 12. 20 13. 5 14. 48
15. 16(1) (2)
注:16题第一空,均正确.
三.解答题(共36分.)
17.解:(Ⅰ), , ...............1分
则,且, ...............3分
所以,,
即. ...............4分
(Ⅱ)令,解得,或 ..........5分
当变化时,,的变化情况如下表所示:
单调递增
单调递减
单调递增
............7分
因此,当时,有极大值,并且极大值为
;
当时,有极小值,并且极小值为
................9分
18.解:(Ⅰ)所有不同选法种数,就是从6名同学中抽出3名的组合数,
所以选法种数为
; ................2分
(Ⅱ)从6名同学抽出的3名中至少有1名女同学,包括1名女同学2
名男同学和2名女同学1名男同学两种情况,所以选法种数为
, ................4分
又这3名同学分别在周五、周六、周日进行宣讲,
所以选法种数为
.....6分
19.解:(Ⅰ),,由已知可得, ........1分
,即, ........2分
所以, ........3分
经检验符合题意,所以 ........4分
(Ⅱ)原不等式转化为,
设,那么,........5分
令, 解得.
当变化时,,的变化情况如下表所示:
单调递减
单调递增
................6分
所以,当时,取得最小值.
所以, ................8分
即,
所以. ................9分
20.解:(Ⅰ)函数的定义域为,
...........2分
①当时,,所以在上单调递增; ...3分
②当时,,解得.
当变化时,,的变化情况如下表所示:
单调递减
单调递增
所以,在上单调递减,在单调递增. ...........5分
综上:当时,在上单调递增;
当时,在上单调递减,在上单调递增.
(Ⅱ)当时,在上单调递增,且,
所以有一个零点;
当时,由(Ⅰ)知,在上单调递增,
且,,
所以存在唯一,使得,
所以有一个零点;
当时,由(Ⅰ)知,在上单调递减,
在上单调递增,所以,则
①,即,,
所以没有零点;
②,即,,
当时,,
所以有一个零点;
③,即,此时,
一方面,,又在上单调递增,
所以存在唯一,使得;
另一方面,,取,则,
令,则,
由于,所以,在单调递减.
所以,.
由于在上单调递减,且,,
所以存在唯一,使得,
所以,当时,在有两个零点.
综上:或,有个零点;
,有个零点;
,有个零点. ..............12分
(其他解法,酌情给分.)
高二数学(A卷)第9页共4页
同课章节目录
