8.6.3(1)平面与平面垂直的判定-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册复习巩固训练Word含答案
文档属性
| 名称 | 8.6.3(1)平面与平面垂直的判定-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册复习巩固训练Word含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 294.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 10:08:12 | ||
图片预览



文档简介
8.6.3(1)平面与平面垂直的判定
一、知识梳理
1.二面角及平面角:
⑴二面角:从一条直线出发的两个_________所组成的图形叫做二面角。二面角的范围是___.
⑵平面角:在二面角的棱上任取一点O,以点O为垂足,在半平面和内分别作____于棱的射线OA和OB,则射线OA和OB构成的叫做二面角的平面角。
2.两个平面互相垂直的定义:
两个平面相交,如果它们所成的二面角是__________,就说这两个平面互相垂直。
3.两个平面互相垂直的判定定理:
如果一个平面过另一个平面的____,那么这两个平面垂直。
二、重要题型
知识点一:二面角
1.如图,AB是圆的直径,PA垂直于圆所在的平面,C是圆上一点(不同于A、B)且PA=AC,则二面角P?BC?A的大小为( )
A.60° B.30° C.45° D.15°
2.三棱锥的顶点在底面的射影为底面正三角形的中心,高是,侧棱长为,那么侧面与底面所成的二面角是( )
A.60° B.30° C.45° D.75°
知识点二:平面与平面垂直的判定
3.如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A,B的任意一点,则图中互相垂直的平面共有( )
A.2对 B.3对 C.4对 D.5对
4.设有直线m,n和平面α,β,则下列结论中正确的是( )
①若m⊥n,m?α,n?β,则α⊥β;②若m∥n,n⊥β,m?α,则α⊥β;
③若m⊥n,α∩β=m,n?α,则α⊥β;④若m⊥α,n⊥β,m⊥n,则α⊥β.
A.①③ B.②④ C.①④ D.②③
知识点三:平面与平面垂直的证明
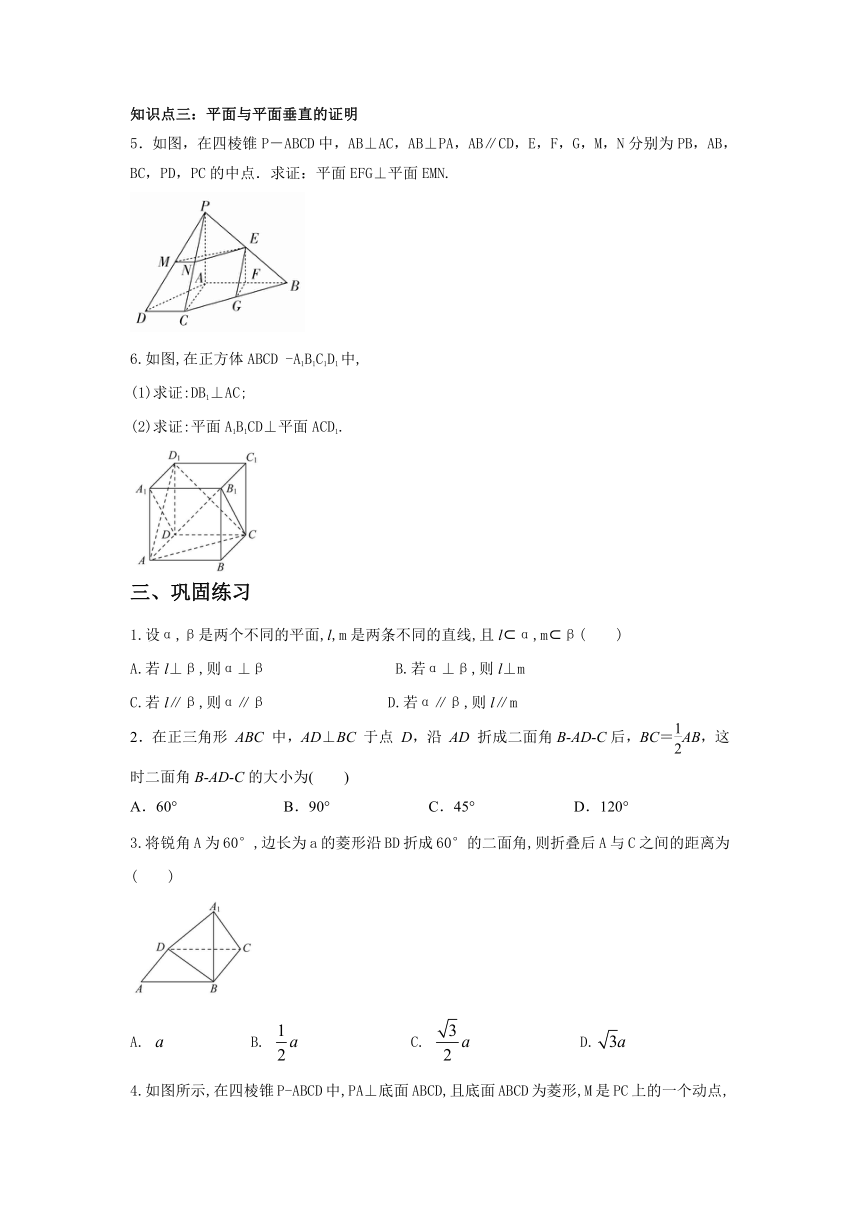
5.如图,在四棱锥P-ABCD中,AB⊥AC,AB⊥PA,AB∥CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点.求证:平面EFG⊥平面EMN.
6.如图,在正方体ABCD -A1B1C1D1中,
(1)求证:DB1⊥AC;
(2)求证:平面A1B1CD⊥平面ACD1.
三、巩固练习
1.设α,β是两个不同的平面,l,m是两条不同的直线,且l?α,m?β( )
A.若l⊥β,则α⊥β B.若α⊥β,则l⊥m
C.若l∥β,则α∥β D.若α∥β,则l∥m
2.在正三角形 ABC 中,AD⊥BC 于点 D,沿 AD 折成二面角B?AD?C后,BC=AB,这时二面角B?AD?C的大小为( )
A.60° B.90° C.45° D.120°
3.将锐角A为60°,边长为a的菱形沿BD折成60°的二面角,则折叠后A与C之间的距离为( )
A. B. C. D.
4.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD为菱形,M是PC上的一个动点,若要使得平面MBD⊥平面PCD,则应补充的一个条件可以是( )
A.MD⊥MB B.MD⊥PC C.AB⊥AD D.BM⊥PC
5.如图,△ABC是等腰直角三角形,∠BAC=90°,AB=AC=1,将△ABC沿斜线BC上的高AD折叠,使平面ABD⊥平面ACD,则BC=________.
6.在二面角α-l-β中,A∈α,AB⊥平面β于点B,BC⊥平面α于点C.若AB=6,
BC=3,则二面角α-l-β的平面角的大小为________.
7.如图,P是二面角α-AB-β的棱AB上一点,分别在α,β上引射线PM,PN,截PM=PN.若∠BPM=∠BPN=45°,∠MPN=60°,则二面角α-AB-β的大小是________.
8.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AB∥CD,AB⊥AD,且CD=2AB.
(1)若AB=AD,直线PB与CD所成的角为45°,求二面角P-CD-B的大小;
(2)若E为线段PC上一点,试确定点E的位置,使得平面EBD⊥平面ABCD,并说明理由.
9.如图,在三棱台DEF-ABC中, AB=2DE,G,H分别为AC,BC的中点.
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
8.6.3(1)平面与平面垂直的判定 答案
一、知识梳理
1. ⑴半平面, .⑵垂直.
2. 直二面角。
3. 垂线
二、重要题型
1.C 由条件得:PA⊥BC,AC⊥BC,又PA∩AC=C,∴BC⊥平面PAC,∴∠PCA为二面角P?BC?A的平面角.在Rt△PAC中,由PA=AC得∠PCA=45°,故选C.
2.A. 如图,设O为底面正三角形的中心,则PO⊥平面ABC,所以.
过O作OM⊥BC于M,连接PM,则有PM⊥BC,所以∠PMO即为侧面与底面所成的二面角.
在直角△CMO中, ,所以在直角△MPO中, ,
所以,所以∠PMO=60°. .
3.B 如图所示.
因为PA⊥平面ACB,PA?平面PAC,PA?平面PAB,所以平面PAC⊥平面ACB,
平面PAB⊥平面ACB.因为PA⊥平面ACB,CB?平面ACB,所以PA⊥CB.又AC⊥CB,
且PA∩AC=A,所以CB⊥平面PAC.又CB?平面PCB,所以平面PAC⊥平面PCB.
共有:平面PAC⊥平面ACB,平面PAB⊥平面ACB,平面PAC⊥平面PCB.故选B.
4.B ①错误,当两平面不垂直时,也能在两个平面内找到互相垂直的直线;③错误,当两平面不垂直时,在一个平面内可以找到无数条直线与两平面的交线垂直.
5.证明:∵E,F分别为PB,AB的中点,∴EF∥PA.∵AB⊥PA,∴AB⊥EF.同理,AB⊥FG.
∵EF∩FG=F,EF?平面EFG,FG?平面EFG,∴AB⊥平面EFG.∵M,N分别为PD,PC的中点,∴MN∥CD.∵AB∥CD,∴MN∥AB,∴MN⊥平面EFG.∵MN?平面EMN,∴平面EFG⊥平面EMN.
6.证明:(1)连接BD、B1D1, 因为DD1⊥平面ABCD,AC?平面ABCD,
所以DD1⊥AC,又AC⊥BD,BD∩DD1=D,BD、DD1?平面DBB1D1,所以AC⊥平面DBB1D1,
又DB1?平面DBB1D1,所以DB1⊥AC.
(2)由(1)同理可得DB1⊥AD1,又AD1∩AC=A,AD1,AC?平面ACD1,
所以DB1⊥平面ACD1,又DB1?平面A1B1CD,所以平面A1B1CD⊥平面ACD1.
三、巩固练习
1.A. 因为l⊥β,l?α,所以α⊥β(面面垂直的判定定理),故A正确.
2.A ∠BDC为二面角B?AD?C的平面角,设正三角形ABC的边长为m,则折叠后,BC=m,BD=DC=m,所以∠BDC=60°.
3.C. 设折叠后点A到A1的位置,取BD的中点E,连接A1E,CE. 则BD⊥CE,BD⊥A1E.
于是∠A1EC为二面角A1-BD -C的平面角.故∠A1EC.因为,所以△A1EC是等边三角形.所以.
4.BD. 连接AC,BD,BM,MD.因为在四棱锥P-ABCD中,PA⊥底面ABCD,
且底面各边都相等,M是PC上的一动点,所以BD⊥PA,BD⊥AC,因为PA∩AC=A,
所以BD⊥平面PAC,所以BD⊥PC.所以当DM⊥PC(或BM⊥PC)时,
即有PC⊥平面MBD.而PC属于平面PCD,所以平面MBD⊥平面PCD.
5.1 因为AD⊥BC,所以AD⊥BD,AD⊥CD,所以∠BDC是二面角B?AD?C的平面角,
因为平面ABD⊥平面ACD,所以∠BDC=90°.在△BCD中∠BDC=90°,又AB=AC=1,
所以BD=CD=,所以BC==1.
6.60°或120° 如图,∵AB⊥β,∴AB⊥l.
∵BC⊥α,∴BC⊥l,∴l⊥平面ABC.设平面ABC∩l=D,则∠ADB为二面角α-l-β的平面角或补角.∵AB=6,BC=3,∴∠BAC=30°,∴∠ADB=60°,∴二面角α-l-β的平面角的大小为60°或120°.
7.90° 在α内过点M作MO⊥AB于点O,连接NO,设PM=PN=a.∵∠BPM=∠BPN=45°,∴△OPM≌△OPN,∴NO⊥AB,∴∠MON为二面角α-AB-β的平面角.连接MN.
∵∠MPN=60°,∴MN=a.又MO=NO=a,∴MO2+NO2=MN2,∴∠MON=90°.
8.解:(1)∵AB⊥AD,CD∥AB,∴CD⊥AD,又PA⊥底面ABCD,CD?平面ABCD,∴PA⊥CD.
又PA∩AD=A,∴CD⊥平面PAD,又PD?平面PAD,∴CD⊥PD,∴∠PDA即是二面角P-CD-B的平面角.又直线PB与CD所成的角为45°,∴∠PBA=45°,∴PA=AB.∴在Rt△PAD中,PA=AD,∴∠PDA=45°,即二面角P-CD-B的大小为45°.
(2)当点E在线段PC上,且满足PE∶EC=1∶2时,平面EBD⊥平面ABCD.理由如下:
连接AC交BD于点O,连接EO.由△AOB∽△COD,且CD=2AB,得CO=2AO,
∴PE∶EC=AO∶CO=1∶2,∴PA∥EO.∵PA⊥底面ABCD,∴EO⊥底面ABCD.
又EO?平面EBD,∴平面EBD⊥平面ABCD.∴在线段PC上存在点E,满足PE∶EC=1∶2时,平面EBD⊥平面ABCD.
9.证明:(1)如图所示,连接DG,设CD∩GF=M,连接MH. 在三棱台DEF-ABC中,AB=2DE,
所以AC=2DF.因为G是AC的中点,所以DF∥GC,且DF=GC,所以四边形CFDG是平行四边形,
所以DM=MC.因为BH=HC,所以MH∥BD.又BD?平面FGH,MH?平面FGH,所以BD∥平面FGH.
(2)因为G,H分别为AC,BC的中点,所以GH∥AB.因为AB⊥BC,所以GH⊥BC.又H为BC的中点,所以EF∥HC,EF=HC,所以四边形EFCH是平行四边形,所以CF∥HE.因为CF⊥BC,所以HE⊥BC.
又HE,GH?平面EGH,HE∩GH=H,所以BC⊥平面EGH.又BC?平面BCD,
所以平面BCD⊥平面EGH.
一、知识梳理
1.二面角及平面角:
⑴二面角:从一条直线出发的两个_________所组成的图形叫做二面角。二面角的范围是___.
⑵平面角:在二面角的棱上任取一点O,以点O为垂足,在半平面和内分别作____于棱的射线OA和OB,则射线OA和OB构成的叫做二面角的平面角。
2.两个平面互相垂直的定义:
两个平面相交,如果它们所成的二面角是__________,就说这两个平面互相垂直。
3.两个平面互相垂直的判定定理:
如果一个平面过另一个平面的____,那么这两个平面垂直。
二、重要题型
知识点一:二面角
1.如图,AB是圆的直径,PA垂直于圆所在的平面,C是圆上一点(不同于A、B)且PA=AC,则二面角P?BC?A的大小为( )
A.60° B.30° C.45° D.15°
2.三棱锥的顶点在底面的射影为底面正三角形的中心,高是,侧棱长为,那么侧面与底面所成的二面角是( )
A.60° B.30° C.45° D.75°
知识点二:平面与平面垂直的判定
3.如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A,B的任意一点,则图中互相垂直的平面共有( )
A.2对 B.3对 C.4对 D.5对
4.设有直线m,n和平面α,β,则下列结论中正确的是( )
①若m⊥n,m?α,n?β,则α⊥β;②若m∥n,n⊥β,m?α,则α⊥β;
③若m⊥n,α∩β=m,n?α,则α⊥β;④若m⊥α,n⊥β,m⊥n,则α⊥β.
A.①③ B.②④ C.①④ D.②③
知识点三:平面与平面垂直的证明
5.如图,在四棱锥P-ABCD中,AB⊥AC,AB⊥PA,AB∥CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点.求证:平面EFG⊥平面EMN.
6.如图,在正方体ABCD -A1B1C1D1中,
(1)求证:DB1⊥AC;
(2)求证:平面A1B1CD⊥平面ACD1.
三、巩固练习
1.设α,β是两个不同的平面,l,m是两条不同的直线,且l?α,m?β( )
A.若l⊥β,则α⊥β B.若α⊥β,则l⊥m
C.若l∥β,则α∥β D.若α∥β,则l∥m
2.在正三角形 ABC 中,AD⊥BC 于点 D,沿 AD 折成二面角B?AD?C后,BC=AB,这时二面角B?AD?C的大小为( )
A.60° B.90° C.45° D.120°
3.将锐角A为60°,边长为a的菱形沿BD折成60°的二面角,则折叠后A与C之间的距离为( )
A. B. C. D.
4.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD为菱形,M是PC上的一个动点,若要使得平面MBD⊥平面PCD,则应补充的一个条件可以是( )
A.MD⊥MB B.MD⊥PC C.AB⊥AD D.BM⊥PC
5.如图,△ABC是等腰直角三角形,∠BAC=90°,AB=AC=1,将△ABC沿斜线BC上的高AD折叠,使平面ABD⊥平面ACD,则BC=________.
6.在二面角α-l-β中,A∈α,AB⊥平面β于点B,BC⊥平面α于点C.若AB=6,
BC=3,则二面角α-l-β的平面角的大小为________.
7.如图,P是二面角α-AB-β的棱AB上一点,分别在α,β上引射线PM,PN,截PM=PN.若∠BPM=∠BPN=45°,∠MPN=60°,则二面角α-AB-β的大小是________.
8.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AB∥CD,AB⊥AD,且CD=2AB.
(1)若AB=AD,直线PB与CD所成的角为45°,求二面角P-CD-B的大小;
(2)若E为线段PC上一点,试确定点E的位置,使得平面EBD⊥平面ABCD,并说明理由.
9.如图,在三棱台DEF-ABC中, AB=2DE,G,H分别为AC,BC的中点.
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
8.6.3(1)平面与平面垂直的判定 答案
一、知识梳理
1. ⑴半平面, .⑵垂直.
2. 直二面角。
3. 垂线
二、重要题型
1.C 由条件得:PA⊥BC,AC⊥BC,又PA∩AC=C,∴BC⊥平面PAC,∴∠PCA为二面角P?BC?A的平面角.在Rt△PAC中,由PA=AC得∠PCA=45°,故选C.
2.A. 如图,设O为底面正三角形的中心,则PO⊥平面ABC,所以.
过O作OM⊥BC于M,连接PM,则有PM⊥BC,所以∠PMO即为侧面与底面所成的二面角.
在直角△CMO中, ,所以在直角△MPO中, ,
所以,所以∠PMO=60°. .
3.B 如图所示.
因为PA⊥平面ACB,PA?平面PAC,PA?平面PAB,所以平面PAC⊥平面ACB,
平面PAB⊥平面ACB.因为PA⊥平面ACB,CB?平面ACB,所以PA⊥CB.又AC⊥CB,
且PA∩AC=A,所以CB⊥平面PAC.又CB?平面PCB,所以平面PAC⊥平面PCB.
共有:平面PAC⊥平面ACB,平面PAB⊥平面ACB,平面PAC⊥平面PCB.故选B.
4.B ①错误,当两平面不垂直时,也能在两个平面内找到互相垂直的直线;③错误,当两平面不垂直时,在一个平面内可以找到无数条直线与两平面的交线垂直.
5.证明:∵E,F分别为PB,AB的中点,∴EF∥PA.∵AB⊥PA,∴AB⊥EF.同理,AB⊥FG.
∵EF∩FG=F,EF?平面EFG,FG?平面EFG,∴AB⊥平面EFG.∵M,N分别为PD,PC的中点,∴MN∥CD.∵AB∥CD,∴MN∥AB,∴MN⊥平面EFG.∵MN?平面EMN,∴平面EFG⊥平面EMN.
6.证明:(1)连接BD、B1D1, 因为DD1⊥平面ABCD,AC?平面ABCD,
所以DD1⊥AC,又AC⊥BD,BD∩DD1=D,BD、DD1?平面DBB1D1,所以AC⊥平面DBB1D1,
又DB1?平面DBB1D1,所以DB1⊥AC.
(2)由(1)同理可得DB1⊥AD1,又AD1∩AC=A,AD1,AC?平面ACD1,
所以DB1⊥平面ACD1,又DB1?平面A1B1CD,所以平面A1B1CD⊥平面ACD1.
三、巩固练习
1.A. 因为l⊥β,l?α,所以α⊥β(面面垂直的判定定理),故A正确.
2.A ∠BDC为二面角B?AD?C的平面角,设正三角形ABC的边长为m,则折叠后,BC=m,BD=DC=m,所以∠BDC=60°.
3.C. 设折叠后点A到A1的位置,取BD的中点E,连接A1E,CE. 则BD⊥CE,BD⊥A1E.
于是∠A1EC为二面角A1-BD -C的平面角.故∠A1EC.因为,所以△A1EC是等边三角形.所以.
4.BD. 连接AC,BD,BM,MD.因为在四棱锥P-ABCD中,PA⊥底面ABCD,
且底面各边都相等,M是PC上的一动点,所以BD⊥PA,BD⊥AC,因为PA∩AC=A,
所以BD⊥平面PAC,所以BD⊥PC.所以当DM⊥PC(或BM⊥PC)时,
即有PC⊥平面MBD.而PC属于平面PCD,所以平面MBD⊥平面PCD.
5.1 因为AD⊥BC,所以AD⊥BD,AD⊥CD,所以∠BDC是二面角B?AD?C的平面角,
因为平面ABD⊥平面ACD,所以∠BDC=90°.在△BCD中∠BDC=90°,又AB=AC=1,
所以BD=CD=,所以BC==1.
6.60°或120° 如图,∵AB⊥β,∴AB⊥l.
∵BC⊥α,∴BC⊥l,∴l⊥平面ABC.设平面ABC∩l=D,则∠ADB为二面角α-l-β的平面角或补角.∵AB=6,BC=3,∴∠BAC=30°,∴∠ADB=60°,∴二面角α-l-β的平面角的大小为60°或120°.
7.90° 在α内过点M作MO⊥AB于点O,连接NO,设PM=PN=a.∵∠BPM=∠BPN=45°,∴△OPM≌△OPN,∴NO⊥AB,∴∠MON为二面角α-AB-β的平面角.连接MN.
∵∠MPN=60°,∴MN=a.又MO=NO=a,∴MO2+NO2=MN2,∴∠MON=90°.
8.解:(1)∵AB⊥AD,CD∥AB,∴CD⊥AD,又PA⊥底面ABCD,CD?平面ABCD,∴PA⊥CD.
又PA∩AD=A,∴CD⊥平面PAD,又PD?平面PAD,∴CD⊥PD,∴∠PDA即是二面角P-CD-B的平面角.又直线PB与CD所成的角为45°,∴∠PBA=45°,∴PA=AB.∴在Rt△PAD中,PA=AD,∴∠PDA=45°,即二面角P-CD-B的大小为45°.
(2)当点E在线段PC上,且满足PE∶EC=1∶2时,平面EBD⊥平面ABCD.理由如下:
连接AC交BD于点O,连接EO.由△AOB∽△COD,且CD=2AB,得CO=2AO,
∴PE∶EC=AO∶CO=1∶2,∴PA∥EO.∵PA⊥底面ABCD,∴EO⊥底面ABCD.
又EO?平面EBD,∴平面EBD⊥平面ABCD.∴在线段PC上存在点E,满足PE∶EC=1∶2时,平面EBD⊥平面ABCD.
9.证明:(1)如图所示,连接DG,设CD∩GF=M,连接MH. 在三棱台DEF-ABC中,AB=2DE,
所以AC=2DF.因为G是AC的中点,所以DF∥GC,且DF=GC,所以四边形CFDG是平行四边形,
所以DM=MC.因为BH=HC,所以MH∥BD.又BD?平面FGH,MH?平面FGH,所以BD∥平面FGH.
(2)因为G,H分别为AC,BC的中点,所以GH∥AB.因为AB⊥BC,所以GH⊥BC.又H为BC的中点,所以EF∥HC,EF=HC,所以四边形EFCH是平行四边形,所以CF∥HE.因为CF⊥BC,所以HE⊥BC.
又HE,GH?平面EGH,HE∩GH=H,所以BC⊥平面EGH.又BC?平面BCD,
所以平面BCD⊥平面EGH.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
