2.2.1 综合法和分析法-2020-2021学年人教A版高中数学选修2-2课件(共22张PPT)
文档属性
| 名称 | 2.2.1 综合法和分析法-2020-2021学年人教A版高中数学选修2-2课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 813.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 11:35:01 | ||
图片预览




文档简介
(共22张PPT)
直接证明
2.2直接证明与间接证明
教学目标
结合已经学过的数学实例,了解直接证明的两种基本方法:分析法和综合法;了解分析法和综合法的思考过程、特点.
教学重点:会用综合法证明问题;了解综合法的思考过程.
教学难点:根据问题的特点,结合综合法的思考过程、特点,选择适当的证明方法.
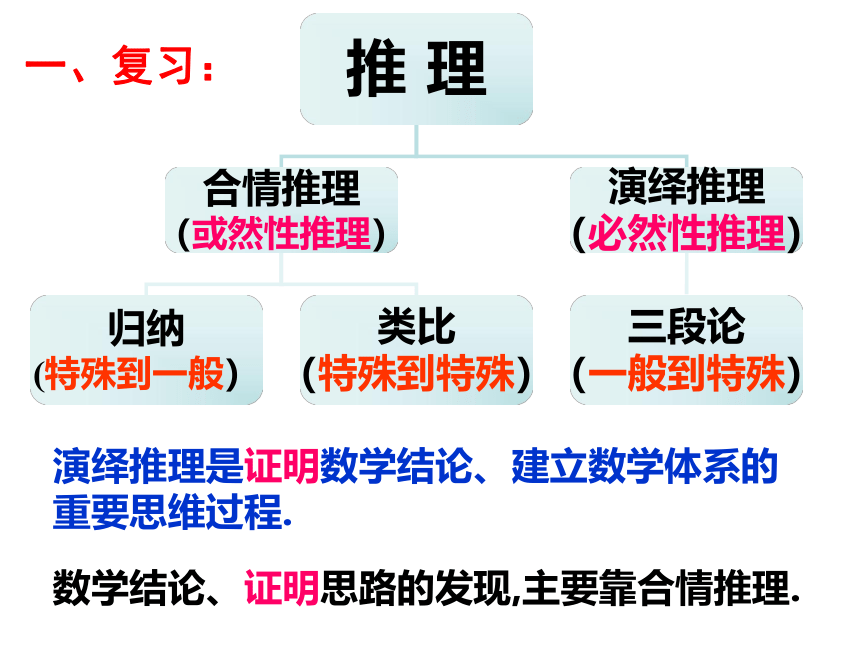
推
理
合情推理
(或然性推理)
演绎推理
(必然性推理)
归纳
(特殊到一般)
类比
(特殊到特殊)
三段论
(一般到特殊)
一、复习:
演绎推理是证明数学结论、建立数学体系的重要思维过程.
数学结论、证明思路的发现,主要靠合情推理.
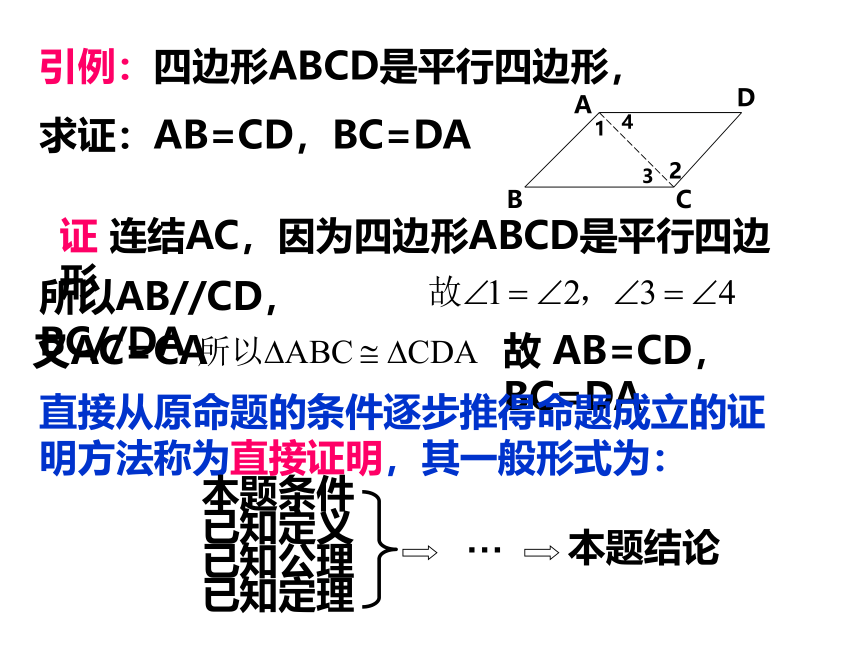
引例:四边形ABCD是平行四边形,
求证:AB=CD,BC=DA
A
B
C
D
1
3
4
2
证
连结AC,因为四边形ABCD是平行四边形
所以AB//CD,BC//DA
又AC=CA
故
AB=CD,BC=DA
直接从原命题的条件逐步推得命题成立的证明方法称为直接证明,其一般形式为:
本题条件
已知定义
已知定理
已知公理
本题结论
…
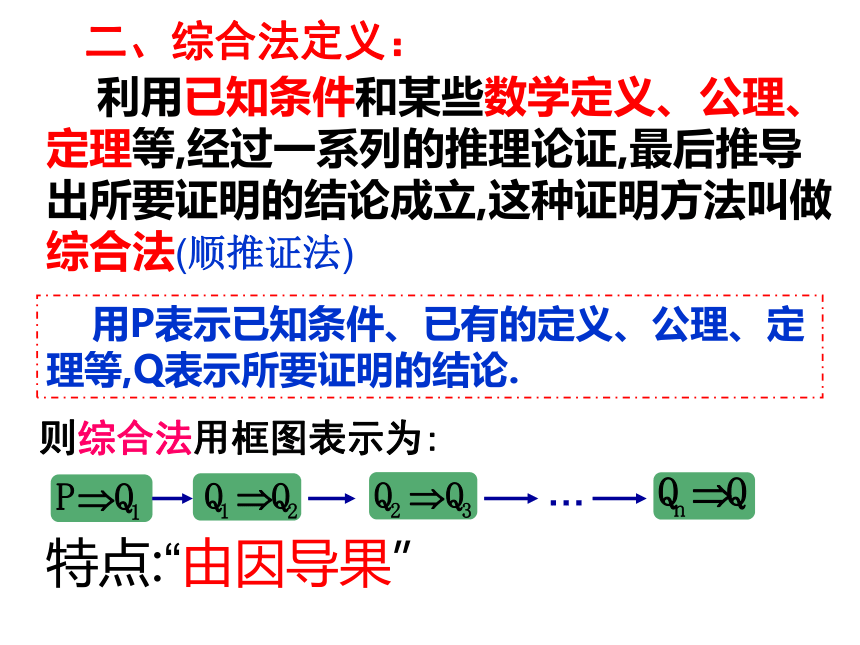
用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.
则综合法用框图表示为:
…
特点:“由因导果”
二、综合法定义:
利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法(顺推证法)
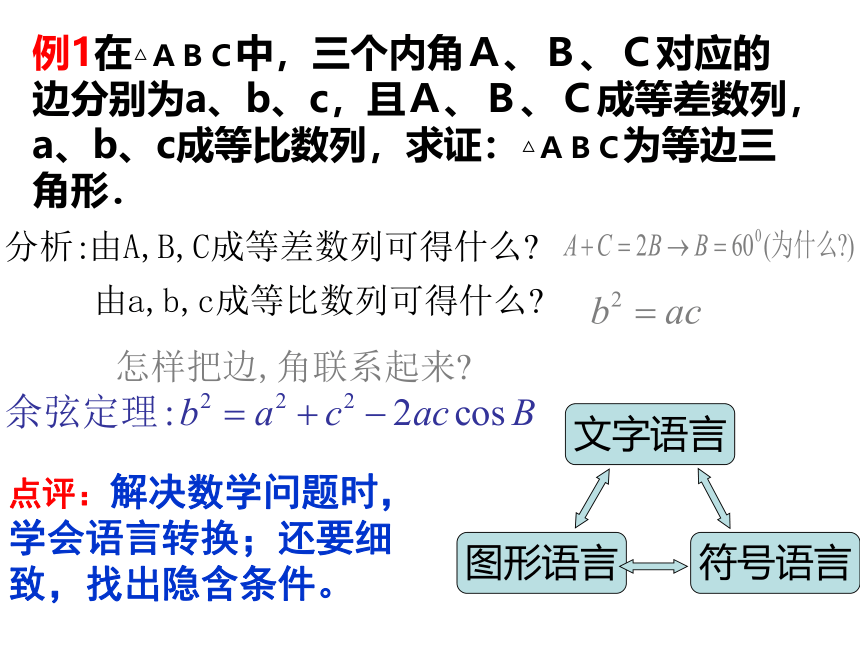
例1在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证:△ABC为等边三角形.
符号语言
图形语言
文字语言
点评:解决数学问题时,学会语言转换;还要细致,找出隐含条件。
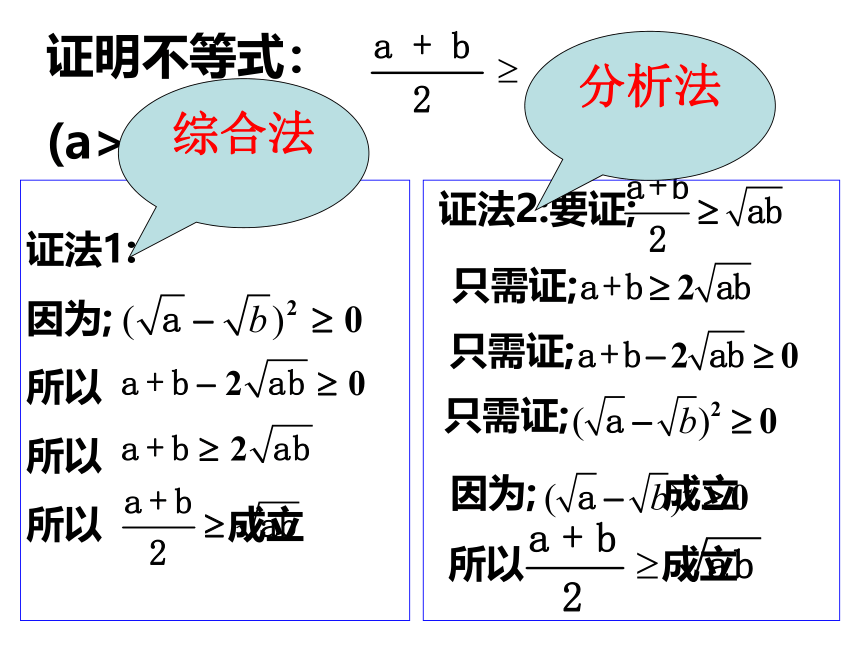
证明不等式:
(a>0,b>0).
证法1:
因为;
所以
所以
所以
成立
证法2:要证;
只需证;
只需证;
只需证;
因为;
成立
所以
成立
综合法
分析法
一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法(也叫逆推证法或执果索因法).
特点:执果索因.
用框图表示分析法的思考过程、特点.
得到一个明显成立的结论
…
三、分析法定义:
用分析法论证“若A则B”这个命题的模式是:
练习、求证:
证法一:为了证明
成立
因为
所以只需证明
成立
展开得
即
因为
成立,所以
成立
证法二:
练一练:
请结合上述例子和自己感受,说说综合法
和分析法的各自特点和它们的适用情况。
(1)综合法:
由因导果,当条件明确,思路清晰时适用;
(2)分析法:
执果索因,当条件多,入手难,思路乱时适用。
(3)综合法是分析法的逆过程。
已知条件
结论
结论
已知条件
例:如图,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F,求证
AF⊥SC
F
E
S
C
B
A
证明:要证AF⊥SC
只需证:SC⊥平面AEF
只需证:AE⊥SC
只需证:AE⊥平面SBC
只需证:AE⊥BC
只需证:BC⊥平面SAB
只需证:BC⊥SA
只需证:SA⊥平面ABC
因为:SA⊥平面ABC成立
所以.
AF⊥SC成立
证法二:∵
SA⊥平面ABC
∴
AE⊥BC
又∵AE⊥SB,且BC∩SB=B
∴
AE⊥平面SBC
∴
AE⊥SC
又∵EF⊥SC,且AE∩EF=E
∴
SC⊥平面AEF
∴
AF⊥SC
∴BC⊥SA
∴
BC⊥平面SAB
又∵AB⊥BC,且AB∩SA=A
直接证明(数学理论)
上述两种证法有什么异同?
都是直接证明
证法1
从已知条件出发,以已知的定义、公理、定理为依据,逐步下推,直到推出要证明的结论为止
综合法
相同
不同
证法2
从问题的结论出发,追溯导致结论成立的条件,逐步上溯,直到使结论成立的条件和已知条件吻合为止
分析法
证:
点评:在解决问题时,我们经常把综合法和分析法结合起来使用:根据条件结构特点去转化结论,得到中间结论Q;根据结论的结构特点去转化条件,得到中间结论P,若P可以推出Q,就可以证明结论成立
用P表示已知条件,定义,定理,公理等,用Q表示要证的结论,则上述过程可用框图表示为:
…
…
P
P1
P1
P2
Pn-1
Pn
Qm-1
Qm
Q
Q1
Q1
Q2
四、综合应用:在解决问题时,我们经常把综合法和分析法结合起来使用:根据条件结构特点去转化结论,得到中间结论Q;根据结论的结构特点去转化条件,得到中间结论P,若P可以推出Q,就可以证明结论成立
练一练:
五、小结
1.在数学证明中,综合法和分析法是两种最常用的数学方法,若从已知入手能找到证明的途径,则用综合法,否则用分析法.
2.综合法的每步推理都是寻找必要条件,分析法的每步推理都是寻找充分条件,在解题表述中要注意语言的规范性和逻辑性.
3.综合法和分析法是两种互逆的思维模式,在证明某些较复杂的问题时,常采用分析综合法,用综合法拓展条件,用分析法转化结论,找出已知与结论的连结点.
综合法的特点:由因导果
分析法的特点:执果索因.
上联:由因导果,顺藤摸瓜
下联:执果索因,逆推破案
横批:得心应手
直接证明
2.2直接证明与间接证明
教学目标
结合已经学过的数学实例,了解直接证明的两种基本方法:分析法和综合法;了解分析法和综合法的思考过程、特点.
教学重点:会用综合法证明问题;了解综合法的思考过程.
教学难点:根据问题的特点,结合综合法的思考过程、特点,选择适当的证明方法.
推
理
合情推理
(或然性推理)
演绎推理
(必然性推理)
归纳
(特殊到一般)
类比
(特殊到特殊)
三段论
(一般到特殊)
一、复习:
演绎推理是证明数学结论、建立数学体系的重要思维过程.
数学结论、证明思路的发现,主要靠合情推理.
引例:四边形ABCD是平行四边形,
求证:AB=CD,BC=DA
A
B
C
D
1
3
4
2
证
连结AC,因为四边形ABCD是平行四边形
所以AB//CD,BC//DA
又AC=CA
故
AB=CD,BC=DA
直接从原命题的条件逐步推得命题成立的证明方法称为直接证明,其一般形式为:
本题条件
已知定义
已知定理
已知公理
本题结论
…
用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.
则综合法用框图表示为:
…
特点:“由因导果”
二、综合法定义:
利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法(顺推证法)
例1在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证:△ABC为等边三角形.
符号语言
图形语言
文字语言
点评:解决数学问题时,学会语言转换;还要细致,找出隐含条件。
证明不等式:
(a>0,b>0).
证法1:
因为;
所以
所以
所以
成立
证法2:要证;
只需证;
只需证;
只需证;
因为;
成立
所以
成立
综合法
分析法
一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法(也叫逆推证法或执果索因法).
特点:执果索因.
用框图表示分析法的思考过程、特点.
得到一个明显成立的结论
…
三、分析法定义:
用分析法论证“若A则B”这个命题的模式是:
练习、求证:
证法一:为了证明
成立
因为
所以只需证明
成立
展开得
即
因为
成立,所以
成立
证法二:
练一练:
请结合上述例子和自己感受,说说综合法
和分析法的各自特点和它们的适用情况。
(1)综合法:
由因导果,当条件明确,思路清晰时适用;
(2)分析法:
执果索因,当条件多,入手难,思路乱时适用。
(3)综合法是分析法的逆过程。
已知条件
结论
结论
已知条件
例:如图,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F,求证
AF⊥SC
F
E
S
C
B
A
证明:要证AF⊥SC
只需证:SC⊥平面AEF
只需证:AE⊥SC
只需证:AE⊥平面SBC
只需证:AE⊥BC
只需证:BC⊥平面SAB
只需证:BC⊥SA
只需证:SA⊥平面ABC
因为:SA⊥平面ABC成立
所以.
AF⊥SC成立
证法二:∵
SA⊥平面ABC
∴
AE⊥BC
又∵AE⊥SB,且BC∩SB=B
∴
AE⊥平面SBC
∴
AE⊥SC
又∵EF⊥SC,且AE∩EF=E
∴
SC⊥平面AEF
∴
AF⊥SC
∴BC⊥SA
∴
BC⊥平面SAB
又∵AB⊥BC,且AB∩SA=A
直接证明(数学理论)
上述两种证法有什么异同?
都是直接证明
证法1
从已知条件出发,以已知的定义、公理、定理为依据,逐步下推,直到推出要证明的结论为止
综合法
相同
不同
证法2
从问题的结论出发,追溯导致结论成立的条件,逐步上溯,直到使结论成立的条件和已知条件吻合为止
分析法
证:
点评:在解决问题时,我们经常把综合法和分析法结合起来使用:根据条件结构特点去转化结论,得到中间结论Q;根据结论的结构特点去转化条件,得到中间结论P,若P可以推出Q,就可以证明结论成立
用P表示已知条件,定义,定理,公理等,用Q表示要证的结论,则上述过程可用框图表示为:
…
…
P
P1
P1
P2
Pn-1
Pn
Qm-1
Qm
Q
Q1
Q1
Q2
四、综合应用:在解决问题时,我们经常把综合法和分析法结合起来使用:根据条件结构特点去转化结论,得到中间结论Q;根据结论的结构特点去转化条件,得到中间结论P,若P可以推出Q,就可以证明结论成立
练一练:
五、小结
1.在数学证明中,综合法和分析法是两种最常用的数学方法,若从已知入手能找到证明的途径,则用综合法,否则用分析法.
2.综合法的每步推理都是寻找必要条件,分析法的每步推理都是寻找充分条件,在解题表述中要注意语言的规范性和逻辑性.
3.综合法和分析法是两种互逆的思维模式,在证明某些较复杂的问题时,常采用分析综合法,用综合法拓展条件,用分析法转化结论,找出已知与结论的连结点.
综合法的特点:由因导果
分析法的特点:执果索因.
上联:由因导果,顺藤摸瓜
下联:执果索因,逆推破案
横批:得心应手
