2.2.2 反证法-2020-2021学年人教A版高中数学选修2-2课件(共14张PPT)
文档属性
| 名称 | 2.2.2 反证法-2020-2021学年人教A版高中数学选修2-2课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 486.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-29 11:36:19 | ||
图片预览




文档简介
(共14张PPT)
2.2
直接证明与间接证明
2.2.2
反
证
法
复习
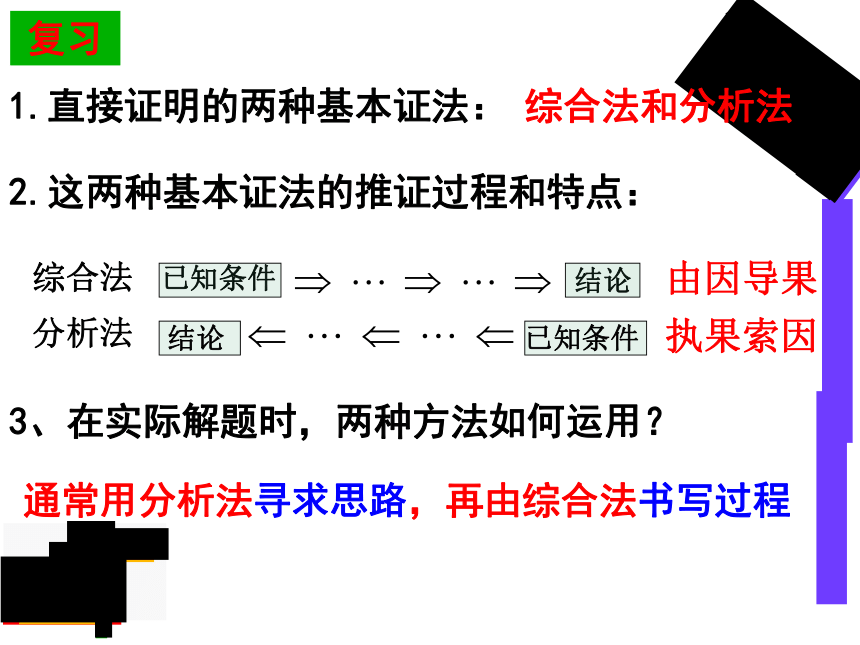
1.直接证明的两种基本证法:
综合法和分析法
2.这两种基本证法的推证过程和特点:
由因导果
执果索因
3、在实际解题时,两种方法如何运用?
通常用分析法寻求思路,再由综合法书写过程
综合法
已知条件
结论
分析法
结论
已知条件
(1)如果有5只鸽子飞进两只鸽笼,至少有3只鸽子在同一只鸽笼,对吗?
(2)A、B、C三个人,A说B撒谎,B说C撒谎,C
说A、B都撒谎。则C在撒谎吗?为什么?
分析:假设C没有撒谎,
则A、B都撒谎.
由A撒谎,
知B没有撒谎.
那么假设C没有撒谎不成立,
则C必定是在撒谎.
这与B撒谎矛盾.
思考?
把这种不是直接从原命题的条件逐步推得命题成立的证明方法称为间接证明
注:反证法是最常见的间接证法,
一般地,假设原命题不成立(即在原命题的条件下,结论不成立),
经过正确的推理,
最后得出矛盾。
因此说明假设错误,从而证明了原命题成立,
这样的证明方法叫做反证法。
理论
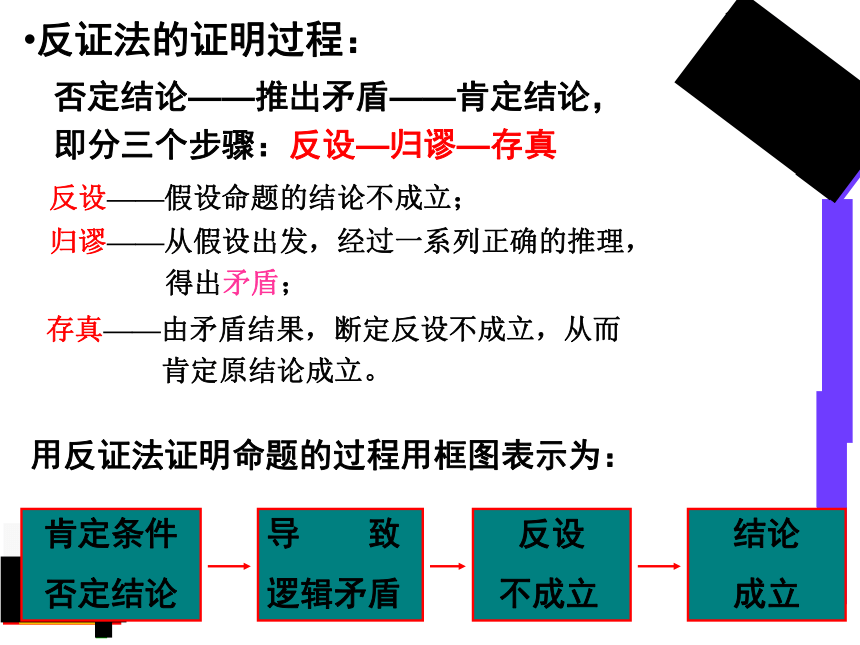
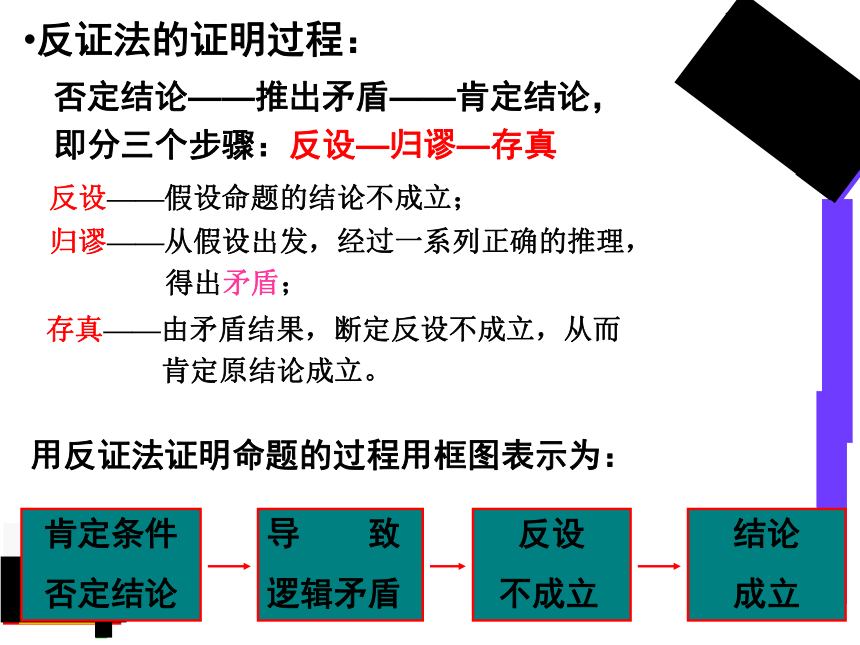
反证法的证明过程:
否定结论——推出矛盾——肯定结论,
即分三个步骤:反设—归谬—存真
反设——假设命题的结论不成立;
存真——由矛盾结果,断定反设不成立,从而
肯定原结论成立。
归谬——从假设出发,经过一系列正确的推理,
````````得出矛盾;
用反证法证明命题的过程用框图表示为:
肯定条件
否定结论
导
致
逻辑矛盾
反设
不成立
结论
成立
例1:已知:整数a的平方能被2整除,
求证:a是偶数。
证明:假设a不是偶数,
则a是奇数,不妨设a=2n+1(n是整数)
∴a2=(2n+1)2=4n2+4n+1=4n(n+1)+1
∴a2是奇数,与已知矛盾。
∴假设不成立,所以a是偶数。
注:直接证明难以下手的命题,改变其思维方向,从反面进行思考,问题可能解决得十分干脆。
例题
反证法的证明过程:
否定结论——推出矛盾——肯定结论,
即分三个步骤:反设—归谬—存真
反设——假设命题的结论不成立;
存真——由矛盾结果,断定反设不成立,从而
肯定原结论成立。
归谬——从假设出发,经过一系列正确的推理,
````````得出矛盾;
用反证法证明命题的过程用框图表示为:
肯定条件
否定结论
导
致
逻辑矛盾
反设
不成立
结论
成立
用反证法证明:圆的两条不是直径的相交弦不能互相平分。
已知:如图,在⊙O中,弦AB、CD交于点P,且AB、CD不是直径.求证:弦AB、CD不被P平分.
例
2
证明:
假设弦AB、CD被P平分,
连结
AD、BD、BC、AC,
D
P
O
B
A
C
因为弦AB、CD被P点平分,所以四边形ABCD是平行四边形
所以
因为
ABCD为圆内接四边形
所以
因此
所以,对角线AB、CD均为直径,
这与已知条件矛盾,即假设不成立
所以,弦AB、CD不被P平分。
用反证法证明:圆的两条不是直径的相交弦不能互相平分。
已知:如图,在⊙O中,弦AB、CD交于点P,且AB、CD不是直径.求证:弦AB、CD不被P平分.
P
O
B
A
D
C
例
2
由于P点一定不是圆心O,连结OP,根据垂径定理的推论,有
所以,弦AB、CD不被P平分。
证明:
假设弦AB、CD被P平分,
即过点P有两条直线与OP都垂直,
这与垂线性质矛盾,即假设不成立
证法二
OP⊥AB,OP⊥CD,
练习:
例3
已知a≠0,证明x的方程ax=b有且只有一个根。
证:由于a
≠0,因此方程至少有一个根x=b/a,
注:结论中的有且只有(有且仅有)形式出现,
是唯一性问题,常用反证法
```
如果方程不只一个根,不妨设x1,x2
(x1
≠x2
)是方程的两个根.
例4:已知x>0,y>0,x+y>2,
求证:
中至少有一个小于2。
分析:所谓至少有一个,就是不可能没有,要证“至少有一个”只要证明它的反面“所有都”不成立即可.
注:“至少”、“至多”
型命题常用反证法
归纳总结:
三个步骤:反设—归谬—存真
归缪矛盾:
(1)与已知条件矛盾;
(2)与已有公理、定理、定义矛盾;
(3)自相矛盾。
一般地,假设原命题不成立(即在原命题的条件下,结论不成立),
经过正确的推理,
最后得出矛盾。
因此说明假设错误,从而证明了原命题成立,
这样的证明方法叫做反证法。
(1)直接证明有困难
正难则反!
归纳总结:
哪些命题适宜用反证法加以证明?
牛顿曾经说过:“反证法是数学家最精当的武器之一”
(3)唯一性命题
(2)否定性命题
(4)至多,至少型命题
2.2
直接证明与间接证明
2.2.2
反
证
法
复习
1.直接证明的两种基本证法:
综合法和分析法
2.这两种基本证法的推证过程和特点:
由因导果
执果索因
3、在实际解题时,两种方法如何运用?
通常用分析法寻求思路,再由综合法书写过程
综合法
已知条件
结论
分析法
结论
已知条件
(1)如果有5只鸽子飞进两只鸽笼,至少有3只鸽子在同一只鸽笼,对吗?
(2)A、B、C三个人,A说B撒谎,B说C撒谎,C
说A、B都撒谎。则C在撒谎吗?为什么?
分析:假设C没有撒谎,
则A、B都撒谎.
由A撒谎,
知B没有撒谎.
那么假设C没有撒谎不成立,
则C必定是在撒谎.
这与B撒谎矛盾.
思考?
把这种不是直接从原命题的条件逐步推得命题成立的证明方法称为间接证明
注:反证法是最常见的间接证法,
一般地,假设原命题不成立(即在原命题的条件下,结论不成立),
经过正确的推理,
最后得出矛盾。
因此说明假设错误,从而证明了原命题成立,
这样的证明方法叫做反证法。
理论
反证法的证明过程:
否定结论——推出矛盾——肯定结论,
即分三个步骤:反设—归谬—存真
反设——假设命题的结论不成立;
存真——由矛盾结果,断定反设不成立,从而
肯定原结论成立。
归谬——从假设出发,经过一系列正确的推理,
````````得出矛盾;
用反证法证明命题的过程用框图表示为:
肯定条件
否定结论
导
致
逻辑矛盾
反设
不成立
结论
成立
例1:已知:整数a的平方能被2整除,
求证:a是偶数。
证明:假设a不是偶数,
则a是奇数,不妨设a=2n+1(n是整数)
∴a2=(2n+1)2=4n2+4n+1=4n(n+1)+1
∴a2是奇数,与已知矛盾。
∴假设不成立,所以a是偶数。
注:直接证明难以下手的命题,改变其思维方向,从反面进行思考,问题可能解决得十分干脆。
例题
反证法的证明过程:
否定结论——推出矛盾——肯定结论,
即分三个步骤:反设—归谬—存真
反设——假设命题的结论不成立;
存真——由矛盾结果,断定反设不成立,从而
肯定原结论成立。
归谬——从假设出发,经过一系列正确的推理,
````````得出矛盾;
用反证法证明命题的过程用框图表示为:
肯定条件
否定结论
导
致
逻辑矛盾
反设
不成立
结论
成立
用反证法证明:圆的两条不是直径的相交弦不能互相平分。
已知:如图,在⊙O中,弦AB、CD交于点P,且AB、CD不是直径.求证:弦AB、CD不被P平分.
例
2
证明:
假设弦AB、CD被P平分,
连结
AD、BD、BC、AC,
D
P
O
B
A
C
因为弦AB、CD被P点平分,所以四边形ABCD是平行四边形
所以
因为
ABCD为圆内接四边形
所以
因此
所以,对角线AB、CD均为直径,
这与已知条件矛盾,即假设不成立
所以,弦AB、CD不被P平分。
用反证法证明:圆的两条不是直径的相交弦不能互相平分。
已知:如图,在⊙O中,弦AB、CD交于点P,且AB、CD不是直径.求证:弦AB、CD不被P平分.
P
O
B
A
D
C
例
2
由于P点一定不是圆心O,连结OP,根据垂径定理的推论,有
所以,弦AB、CD不被P平分。
证明:
假设弦AB、CD被P平分,
即过点P有两条直线与OP都垂直,
这与垂线性质矛盾,即假设不成立
证法二
OP⊥AB,OP⊥CD,
练习:
例3
已知a≠0,证明x的方程ax=b有且只有一个根。
证:由于a
≠0,因此方程至少有一个根x=b/a,
注:结论中的有且只有(有且仅有)形式出现,
是唯一性问题,常用反证法
```
如果方程不只一个根,不妨设x1,x2
(x1
≠x2
)是方程的两个根.
例4:已知x>0,y>0,x+y>2,
求证:
中至少有一个小于2。
分析:所谓至少有一个,就是不可能没有,要证“至少有一个”只要证明它的反面“所有都”不成立即可.
注:“至少”、“至多”
型命题常用反证法
归纳总结:
三个步骤:反设—归谬—存真
归缪矛盾:
(1)与已知条件矛盾;
(2)与已有公理、定理、定义矛盾;
(3)自相矛盾。
一般地,假设原命题不成立(即在原命题的条件下,结论不成立),
经过正确的推理,
最后得出矛盾。
因此说明假设错误,从而证明了原命题成立,
这样的证明方法叫做反证法。
(1)直接证明有困难
正难则反!
归纳总结:
哪些命题适宜用反证法加以证明?
牛顿曾经说过:“反证法是数学家最精当的武器之一”
(3)唯一性命题
(2)否定性命题
(4)至多,至少型命题
