吉林省榆树市第一高级中学2011届高三第一次模拟考试数学试题(无答案)
文档属性
| 名称 | 吉林省榆树市第一高级中学2011届高三第一次模拟考试数学试题(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 94.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-06 00:00:00 | ||
图片预览


文档简介
一.选择题:(每题5分共60分)
1.若集合,则等于( )
A B C D {1}
2.函数的图象恒过定点A,且点A在直线上,则的最小值为 ( )
A 12 B 10 C 8 D 14
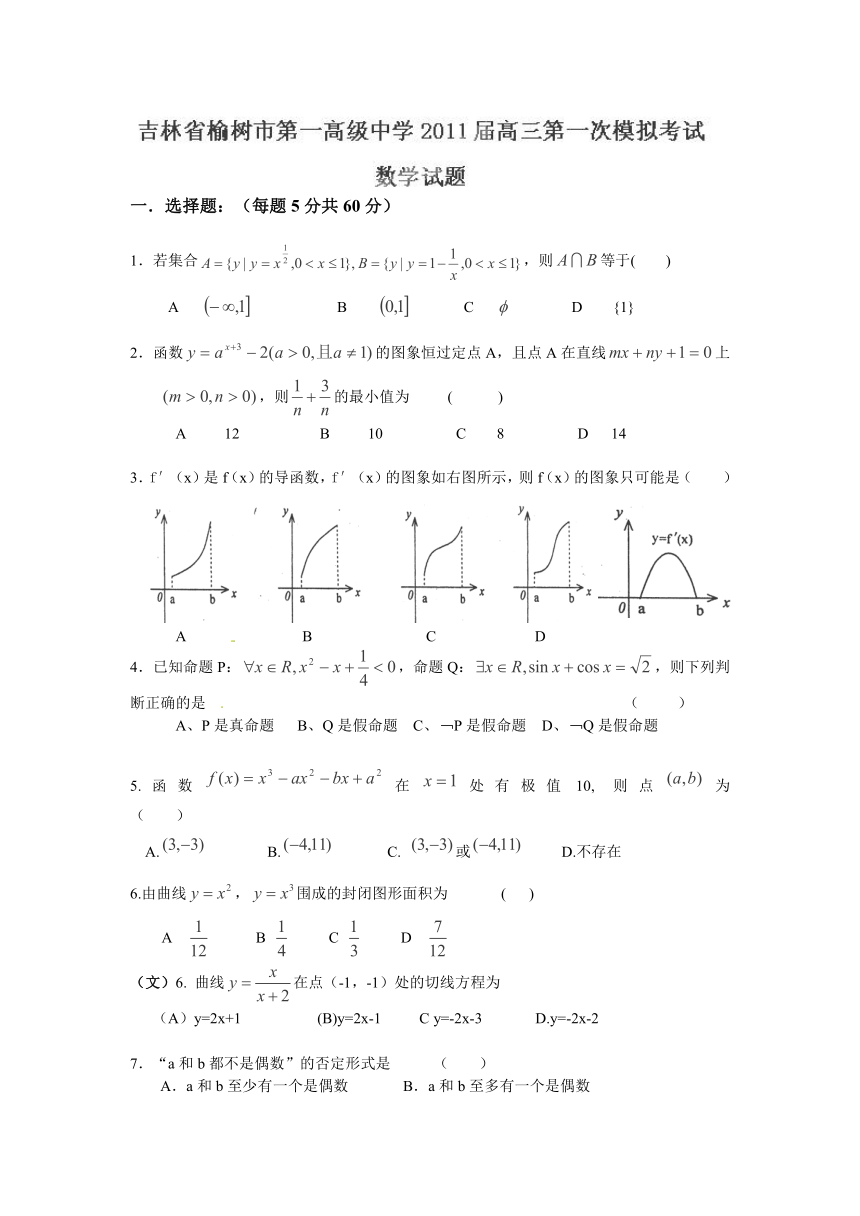
3.f′(x)是f(x)的导函数,f′(x)的图象如右图所示,则f(x)的图象只可能是( )
A B C D
4.已知命题P:,命题Q:,则下列判断正确的是 ( )
A、P是真命题 B、Q是假命题 C、﹁P是假命题 D、﹁Q是假命题
5.函数在处有极值10, 则点为 ( )
A. B. C. 或 D.不存在
6.由曲线,围成的封闭图形面积为 ( )
A B C D
(文)6. 曲线在点(-1,-1)处的切线方程为
(A)y=2x+1 (B)y=2x-1 C y=-2x-3 D.y=-2x-2
7.“a和b都不是偶数”的否定形式是 ( )
A.a和b至少有一个是偶数 B.a和b至多有一个是偶数
C.a是偶数,b不是偶数 D.a和b都是偶数
8. 函数f(x)=lnx-的零点所在的区间是 ( )
A.(0,1) B.(1,e) C.(e,3) D.(3,+∞)
9. 某学校开展研究性学习活动,一组同学获得了下面的一组实验数据:
x 1.99 3 4 5.1 6.12
y 1.5 4.04 7.5 12 18.01
现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )
A.y=2x-2 B.y=()x C.y=log2x D.y=(x2-1)
10. 已知P(x,y)是函数y=ex+x图象上的点,则点P到直线2x-y-3=0的最小距离为( )
A. B. C. D.
11 由下列各组命题构成的"p或q","p且q","非p"形式的复合命题中,p或q为真,p且q为假,非p为真的是 ( )
A p:3是偶数;q:4是奇数 B p:3+2=6;q:4>3
C p:a∈{a,b};q:{a}{a,b} D p:QR;q:N=N*
12.设函数的定义域为,若对于给定的正数,定义函数,则当函数时,定积分的值为( )
A B C D
(文)12.设偶函数满足,则
(A) (B) (C) (D)
二.填空题: (每题5分,共20分)
13. 已知函数f(x)=3x2+2x+1,若∫f(x)dx=2f(a)成立,则a= .
(文) 13.函数,若对一切实数恒成立,则实数的取值范围是 .
14. 已知定义在R上的函数f(x)是偶函数,对x∈R,f(2+x)=f(2-x),当f(-3)=-2时,f(2011)的值为________.
15. 函数f(x)的图象是如下图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0),定义函数g(x)=f(x)·(x-1),则函数g(x)的最大值为________.
(文)15.设函数f(x)=,若f(-4)=f(0),f(-2)=-2,则f(x)的解析式为f(x)=________,关于x的方程f(x)=x的解的个数为________个.
16.以下四个命题,是真命题的有 (把你认为是真命题的序号都填上).
①若p:f(x)=lnx-2+x在区间(1,2)上有一个零点;
q:e0.2>e0.3,则p∧q为假命题;
②当x>1时,f(x)=x2,g(x)=,h(x)=x-2的大小关系是h(x)<g(x)<f(x);
③若f′(x0)=0,则f(x)在x=x0处取得极值;
④若不等式2-3x-2x2>0的解集为P,函数y=+的定义域为Q,则“x ∈P”是“x∈Q”的充分不必要条件.
三.解答题:
17. (10分)给定两个命题,
P:对任意实数都有恒成立;Q:关于的方程有实数根;如果P与Q中有且仅有一个为真命题,求实数的取值范围。
.(12分)是否存在这样的实数a,使函数f(x)=x2+(3a-2)x+a-1在区间[-1,3]上与x轴恒有一个交点,且只有一个交点.若存在,求出范围,若不存在,说明理由.
19.(12分)已知定义在区间(0,+∞)上的函数f(x)满足f()=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;(2)判断f(x)的单调性;(3)若f(3)=-1,解不等式f(|x|)<-2.
20. (12分) 已知函数.
⑴若,求曲线在点处的切线方程;
⑵若函数在其定义域内为增函数,求正实数的取值范围;
21.(12分)在2008年11月4日珠海航展上,中国自主研制的ARJ 21支线客机备受关注,接到了包括美国在内的多国订单.某工厂有216名工人接受了生产1000件该支线客机某零部件的总任务,已知每件零件由4个C型装置和3个H型装置配套组成,每个工人每小时能加工6个C型装置或3个H型装置.现将工人分成两组同时开始加工,每组分别加工一种装置,设加工C型装置的工人有x位,他们加工完C型装置所需时间为g(x),其余工人加工完H型装置所需时间为h(x).(单位:h,时间可不为整数)
(1)写出g(x),h(x)的解析式;
(2)写出这216名工人完成总任务的时间f(x)的解析式;
(3)应怎样分组,才能使完成总任务的时间最少?
22.(12分) 已知函数f(x)=x4+ax3+2x2+b(x∈R),其中a,b∈R.
(1)当a=-时,讨论函数f(x)的单调性;
(2)若函数f(x)仅在x=0时处有极值,求a的取值范围;
(文)22.( 12分)已知函数f(x)=-x3+3x2+9x+a,
(1)求f(x)的单调区间;
(2)若f(x)在区间[-2,2]上的最大值为20,求函数f(x)在该区间上的最小值
1.若集合,则等于( )
A B C D {1}
2.函数的图象恒过定点A,且点A在直线上,则的最小值为 ( )
A 12 B 10 C 8 D 14
3.f′(x)是f(x)的导函数,f′(x)的图象如右图所示,则f(x)的图象只可能是( )
A B C D
4.已知命题P:,命题Q:,则下列判断正确的是 ( )
A、P是真命题 B、Q是假命题 C、﹁P是假命题 D、﹁Q是假命题
5.函数在处有极值10, 则点为 ( )
A. B. C. 或 D.不存在
6.由曲线,围成的封闭图形面积为 ( )
A B C D
(文)6. 曲线在点(-1,-1)处的切线方程为
(A)y=2x+1 (B)y=2x-1 C y=-2x-3 D.y=-2x-2
7.“a和b都不是偶数”的否定形式是 ( )
A.a和b至少有一个是偶数 B.a和b至多有一个是偶数
C.a是偶数,b不是偶数 D.a和b都是偶数
8. 函数f(x)=lnx-的零点所在的区间是 ( )
A.(0,1) B.(1,e) C.(e,3) D.(3,+∞)
9. 某学校开展研究性学习活动,一组同学获得了下面的一组实验数据:
x 1.99 3 4 5.1 6.12
y 1.5 4.04 7.5 12 18.01
现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )
A.y=2x-2 B.y=()x C.y=log2x D.y=(x2-1)
10. 已知P(x,y)是函数y=ex+x图象上的点,则点P到直线2x-y-3=0的最小距离为( )
A. B. C. D.
11 由下列各组命题构成的"p或q","p且q","非p"形式的复合命题中,p或q为真,p且q为假,非p为真的是 ( )
A p:3是偶数;q:4是奇数 B p:3+2=6;q:4>3
C p:a∈{a,b};q:{a}{a,b} D p:QR;q:N=N*
12.设函数的定义域为,若对于给定的正数,定义函数,则当函数时,定积分的值为( )
A B C D
(文)12.设偶函数满足,则
(A) (B) (C) (D)
二.填空题: (每题5分,共20分)
13. 已知函数f(x)=3x2+2x+1,若∫f(x)dx=2f(a)成立,则a= .
(文) 13.函数,若对一切实数恒成立,则实数的取值范围是 .
14. 已知定义在R上的函数f(x)是偶函数,对x∈R,f(2+x)=f(2-x),当f(-3)=-2时,f(2011)的值为________.
15. 函数f(x)的图象是如下图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0),定义函数g(x)=f(x)·(x-1),则函数g(x)的最大值为________.
(文)15.设函数f(x)=,若f(-4)=f(0),f(-2)=-2,则f(x)的解析式为f(x)=________,关于x的方程f(x)=x的解的个数为________个.
16.以下四个命题,是真命题的有 (把你认为是真命题的序号都填上).
①若p:f(x)=lnx-2+x在区间(1,2)上有一个零点;
q:e0.2>e0.3,则p∧q为假命题;
②当x>1时,f(x)=x2,g(x)=,h(x)=x-2的大小关系是h(x)<g(x)<f(x);
③若f′(x0)=0,则f(x)在x=x0处取得极值;
④若不等式2-3x-2x2>0的解集为P,函数y=+的定义域为Q,则“x ∈P”是“x∈Q”的充分不必要条件.
三.解答题:
17. (10分)给定两个命题,
P:对任意实数都有恒成立;Q:关于的方程有实数根;如果P与Q中有且仅有一个为真命题,求实数的取值范围。
.(12分)是否存在这样的实数a,使函数f(x)=x2+(3a-2)x+a-1在区间[-1,3]上与x轴恒有一个交点,且只有一个交点.若存在,求出范围,若不存在,说明理由.
19.(12分)已知定义在区间(0,+∞)上的函数f(x)满足f()=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;(2)判断f(x)的单调性;(3)若f(3)=-1,解不等式f(|x|)<-2.
20. (12分) 已知函数.
⑴若,求曲线在点处的切线方程;
⑵若函数在其定义域内为增函数,求正实数的取值范围;
21.(12分)在2008年11月4日珠海航展上,中国自主研制的ARJ 21支线客机备受关注,接到了包括美国在内的多国订单.某工厂有216名工人接受了生产1000件该支线客机某零部件的总任务,已知每件零件由4个C型装置和3个H型装置配套组成,每个工人每小时能加工6个C型装置或3个H型装置.现将工人分成两组同时开始加工,每组分别加工一种装置,设加工C型装置的工人有x位,他们加工完C型装置所需时间为g(x),其余工人加工完H型装置所需时间为h(x).(单位:h,时间可不为整数)
(1)写出g(x),h(x)的解析式;
(2)写出这216名工人完成总任务的时间f(x)的解析式;
(3)应怎样分组,才能使完成总任务的时间最少?
22.(12分) 已知函数f(x)=x4+ax3+2x2+b(x∈R),其中a,b∈R.
(1)当a=-时,讨论函数f(x)的单调性;
(2)若函数f(x)仅在x=0时处有极值,求a的取值范围;
(文)22.( 12分)已知函数f(x)=-x3+3x2+9x+a,
(1)求f(x)的单调区间;
(2)若f(x)在区间[-2,2]上的最大值为20,求函数f(x)在该区间上的最小值
同课章节目录
