吉林省重点中学2011届高三第一次模拟考试数学(文)试题
文档属性
| 名称 | 吉林省重点中学2011届高三第一次模拟考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 714.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-06 15:26:47 | ||
图片预览



文档简介
一、选择题(本大题共12小题,每小题5分,共计60分)
1.设集合I={―2,―1,0,1,2},A={1,2},B={―2,―1,2},则A(CIB)=( )
A.{0,1,2} B.{1,2} C.{2} D.{1}
2.函数的定义域是 ( )
A. B. C. D.
3.若p:|x+1|>2,q:x>2,,则┐p是┐q成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4. 设a>1,函数f(x)=a|x|的图像大致是 ( )
5.如图是一个几何体的三视图,则此三视图所描述几何体的
表面积为 ( )
A. B.20
C. D.28
6.已知a=(1,2),b=(3,-1)且a+b与a-λb互相垂直,则实数的λ值为 ( )
A.- B.- C. D.
7.过点(,-2)的直线l经过圆x2+y2-2y=0的圆心,则直线l的倾斜角大小为( )
A.150° B. 60° C.30° D. 120°
8.在△ABC中,已知a=2b cosC,那么这个三角形一定是 ( )
A.等边三角形 B.直角三角形 C.等腰三角形 D.等腰直角三角形
9.是R上的单调递增函数,则实数的取值范围为 ( )
A.(1,+∞) B.[4,8] C.(4,8) D.(1,8)
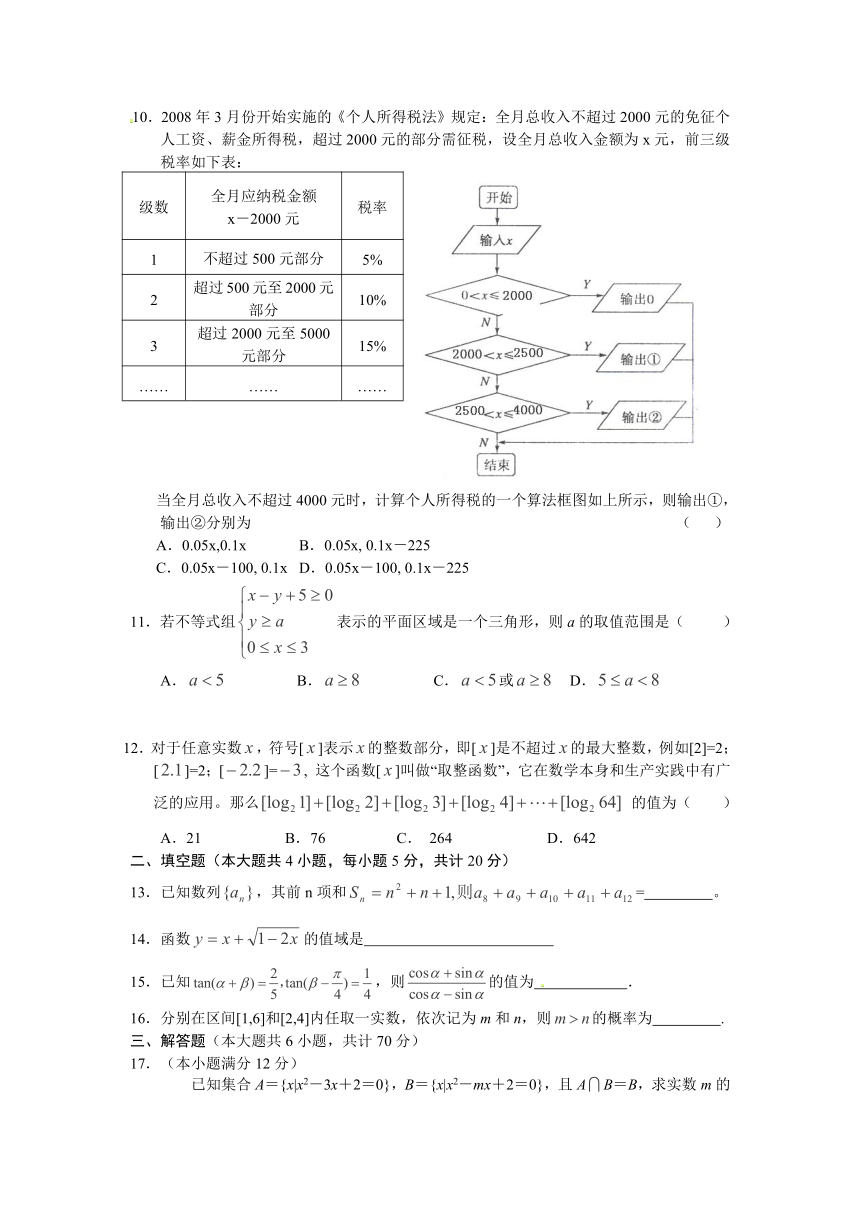
10.2008年3月份开始实施的《个人所得税法》规定:全月总收入不超过2000元的免征个人工资、薪金所得税,超过2000元的部分需征税,设全月总收入金额为x元,前三级税率如下表:
级数 全月应纳税金额x-2000元 税率
1 不超过500元部分 5%
2 超过500元至2000元部分 10%
3 超过2000元至5000元部分 15%
…… …… ……
当全月总收入不超过4000元时,计算个人所得税的一个算法框图如上所示,则输出①,输出②分别为 ( )
A.0.05x,0.1x B.0.05x, 0.1x-225
C.0.05x-100, 0.1x D.0.05x-100, 0.1x-225
11.若不等式组表示的平面区域是一个三角形,则a的取值范围是( )
A. B. C.或 D.
12.对于任意实数,符号[]表示的整数部分,即[]是不超过的最大整数,例如[2]=2;[]=2;[]=, 这个函数[]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。那么 的值为( )
A.21 B.76 C. 264 D.642
二、填空题(本大题共4小题,每小题5分,共计20分)
13.已知数列,其前n项和= 。
14.函数的值域是
15.已知,则的值为 .
16.分别在区间[1,6]和[2,4]内任取一实数,依次记为m和n,则的概率为 .
三、解答题(本大题共6小题,共计70分)
17.(本小题满分12分)
已知集合A={x|x2-3x+2=0},B={x|x2-mx+2=0},且AB=B,求实数m的取值范围。
18.(本小题满分12分)
已知函数(Ⅰ)求证:对于的定义域内的任意两个实数,都有;(Ⅱ)判断的奇偶性,并予以证明.
19.(本小题满分12分)
为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列的前四项,后6组的频数从左到右依次是等差数列的前六项.
(I)求等比数列的通项公式;
(II)求等差数列的通项公式;
(III)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率的大小.
20.(本小题满分12分)
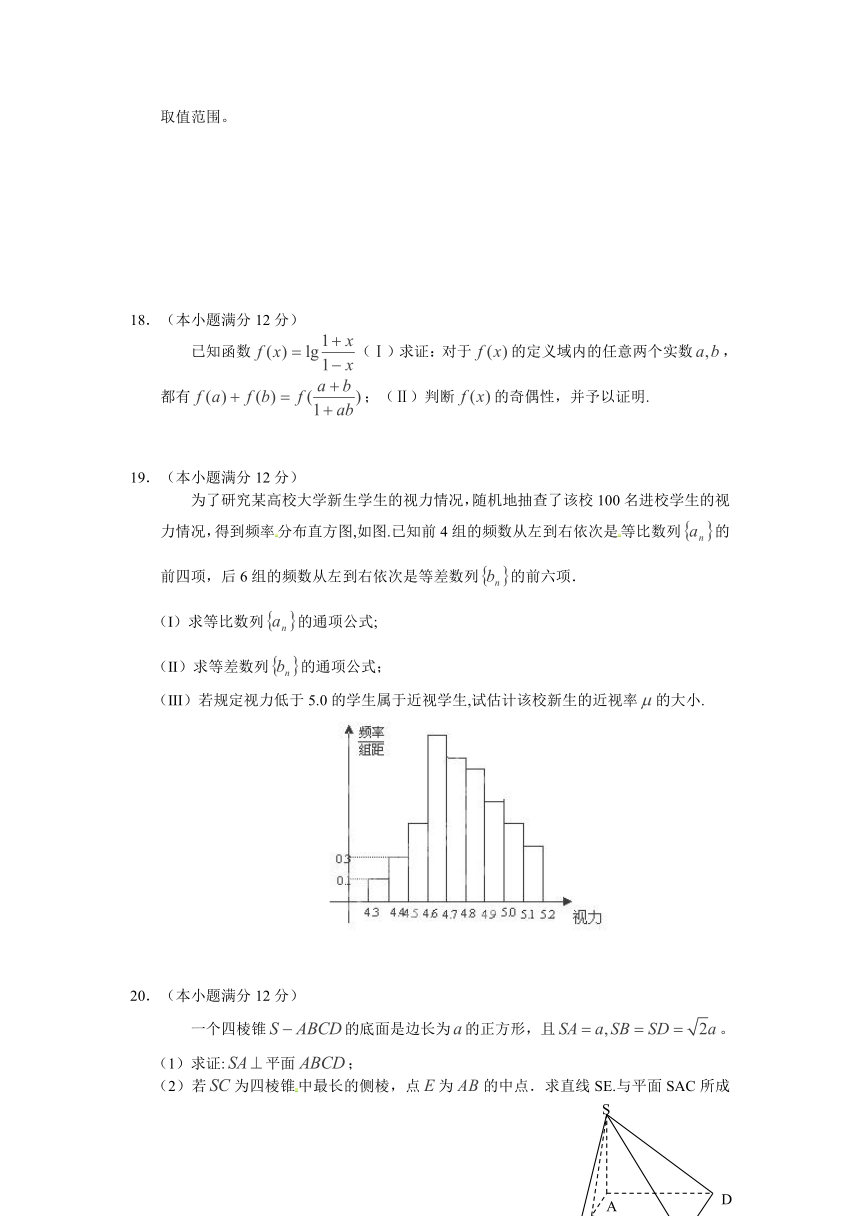
一个四棱锥的底面是边长为的正方形,且。
(1)求证:平面;
(2)若为四棱锥中最长的侧棱,点为的中点.求直线SE.与平面SAC所成角的正弦值。
21.(本小题满分12分)
已知向量,,,.函数,若的图象的一个对称中心与它相邻的一个对称轴之间的距离为1,且过点.
(Ⅰ)求函数的表达式.
(Ⅱ)当时,求函数的单调区间.
选考题:请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。本题满分10分.
22.选修4-1:几何证明选讲
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,
交AC的延长线于点E.OE交AD于点F.
(1)求证:DE是⊙O的切线;
(2)若,求的值.
23. 选修4-4:几何证明选讲
在曲线:上求一点,使它到直线
:的距离最小,并求出该点坐标和最小距离。
24.选修4-5:不等式选讲
已知|x-4|+|3-x|(1)若不等式的解集为空集,求a的范围
(2)若不等式有解,求a的范围
参考答案
∴ m=3 ………………11分
综上所述,m=3或 ……………… 12分
18.(本小题满分12分)已知函数(Ⅰ)求证:对于的定义域内的任意两个实数,
即,所以是奇函数 ………………………12分
19.(本小题满分12分)为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力
EF= SE=(10分)….12分
21.(本小题满分12分)已知向量,,,.函数,若的图象的一个对称中心与它相邻的一个对称轴之间的距离为1,且过点. (Ⅰ)求函数的表达式; (Ⅱ)当时,求函数的单调区间.
Cos∠DOH=cos∠CAB= ……………………6分
设OD=5x,则AB=10x,OH=3x,DH=4x
∴AH=8x AD2=80x2
由△AED∽△ADB可得 AD2=AE·AB=AE·10x ∴AE=8X…………8分
又由△AEF∽△DOF 可得AF∶DF= AE∶OD =;
∴=……10分
23.在曲线:上求一点,使它到直线:的距离最
24.解法一:(1)<1> x≥4 时 (x-4)+(x-3) < a
f(x)=2x-7 在 x≥4上单调递增 x=4时取最小值1。
若要求不等式无解,则 a 小于或等于该最小值即可。即 a ≤ 1 ……2分
<2.> 4>x>3时 (4-x) + (x-3) < a 1 < a
若要求不等式无解,则 a ≤ 1。否则不等式的解集为全集。…………………4分
A
S
C
B
D
(1)
E
F
E
D
C
B
A
O
1.设集合I={―2,―1,0,1,2},A={1,2},B={―2,―1,2},则A(CIB)=( )
A.{0,1,2} B.{1,2} C.{2} D.{1}
2.函数的定义域是 ( )
A. B. C. D.
3.若p:|x+1|>2,q:x>2,,则┐p是┐q成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4. 设a>1,函数f(x)=a|x|的图像大致是 ( )
5.如图是一个几何体的三视图,则此三视图所描述几何体的
表面积为 ( )
A. B.20
C. D.28
6.已知a=(1,2),b=(3,-1)且a+b与a-λb互相垂直,则实数的λ值为 ( )
A.- B.- C. D.
7.过点(,-2)的直线l经过圆x2+y2-2y=0的圆心,则直线l的倾斜角大小为( )
A.150° B. 60° C.30° D. 120°
8.在△ABC中,已知a=2b cosC,那么这个三角形一定是 ( )
A.等边三角形 B.直角三角形 C.等腰三角形 D.等腰直角三角形
9.是R上的单调递增函数,则实数的取值范围为 ( )
A.(1,+∞) B.[4,8] C.(4,8) D.(1,8)
10.2008年3月份开始实施的《个人所得税法》规定:全月总收入不超过2000元的免征个人工资、薪金所得税,超过2000元的部分需征税,设全月总收入金额为x元,前三级税率如下表:
级数 全月应纳税金额x-2000元 税率
1 不超过500元部分 5%
2 超过500元至2000元部分 10%
3 超过2000元至5000元部分 15%
…… …… ……
当全月总收入不超过4000元时,计算个人所得税的一个算法框图如上所示,则输出①,输出②分别为 ( )
A.0.05x,0.1x B.0.05x, 0.1x-225
C.0.05x-100, 0.1x D.0.05x-100, 0.1x-225
11.若不等式组表示的平面区域是一个三角形,则a的取值范围是( )
A. B. C.或 D.
12.对于任意实数,符号[]表示的整数部分,即[]是不超过的最大整数,例如[2]=2;[]=2;[]=, 这个函数[]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。那么 的值为( )
A.21 B.76 C. 264 D.642
二、填空题(本大题共4小题,每小题5分,共计20分)
13.已知数列,其前n项和= 。
14.函数的值域是
15.已知,则的值为 .
16.分别在区间[1,6]和[2,4]内任取一实数,依次记为m和n,则的概率为 .
三、解答题(本大题共6小题,共计70分)
17.(本小题满分12分)
已知集合A={x|x2-3x+2=0},B={x|x2-mx+2=0},且AB=B,求实数m的取值范围。
18.(本小题满分12分)
已知函数(Ⅰ)求证:对于的定义域内的任意两个实数,都有;(Ⅱ)判断的奇偶性,并予以证明.
19.(本小题满分12分)
为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列的前四项,后6组的频数从左到右依次是等差数列的前六项.
(I)求等比数列的通项公式;
(II)求等差数列的通项公式;
(III)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率的大小.
20.(本小题满分12分)
一个四棱锥的底面是边长为的正方形,且。
(1)求证:平面;
(2)若为四棱锥中最长的侧棱,点为的中点.求直线SE.与平面SAC所成角的正弦值。
21.(本小题满分12分)
已知向量,,,.函数,若的图象的一个对称中心与它相邻的一个对称轴之间的距离为1,且过点.
(Ⅰ)求函数的表达式.
(Ⅱ)当时,求函数的单调区间.
选考题:请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。本题满分10分.
22.选修4-1:几何证明选讲
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,
交AC的延长线于点E.OE交AD于点F.
(1)求证:DE是⊙O的切线;
(2)若,求的值.
23. 选修4-4:几何证明选讲
在曲线:上求一点,使它到直线
:的距离最小,并求出该点坐标和最小距离。
24.选修4-5:不等式选讲
已知|x-4|+|3-x|
(2)若不等式有解,求a的范围
参考答案
∴ m=3 ………………11分
综上所述,m=3或 ……………… 12分
18.(本小题满分12分)已知函数(Ⅰ)求证:对于的定义域内的任意两个实数,
即,所以是奇函数 ………………………12分
19.(本小题满分12分)为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力
EF= SE=(10分)….12分
21.(本小题满分12分)已知向量,,,.函数,若的图象的一个对称中心与它相邻的一个对称轴之间的距离为1,且过点. (Ⅰ)求函数的表达式; (Ⅱ)当时,求函数的单调区间.
Cos∠DOH=cos∠CAB= ……………………6分
设OD=5x,则AB=10x,OH=3x,DH=4x
∴AH=8x AD2=80x2
由△AED∽△ADB可得 AD2=AE·AB=AE·10x ∴AE=8X…………8分
又由△AEF∽△DOF 可得AF∶DF= AE∶OD =;
∴=……10分
23.在曲线:上求一点,使它到直线:的距离最
24.解法一:(1)<1> x≥4 时 (x-4)+(x-3) < a
f(x)=2x-7 在 x≥4上单调递增 x=4时取最小值1。
若要求不等式无解,则 a 小于或等于该最小值即可。即 a ≤ 1 ……2分
<2.> 4>x>3时 (4-x) + (x-3) < a 1 < a
若要求不等式无解,则 a ≤ 1。否则不等式的解集为全集。…………………4分
A
S
C
B
D
(1)
E
F
E
D
C
B
A
O
同课章节目录
